Il nostro caro amico Andy, solutore più che abile di molti quiz proposti, ha voluto analizzare con maggiori dettagli il problema dell'esagono con i lati uguali e paralleli a due a due, ma con gli angoli ai vertici diversi tra loro. Così facendo ha trovato risultati più compatti, utilizzando altre formule relative alle aree. Pensiamo che valga la pena proporvele, dato che sono un ghiotto boccone per chi ama la geometria.

Un grazie di cuore ad Andy!

P.S. Chiedo scusa per tutte quelle cornici intorno a molte parti del testo ma, data l'impossibilità di copiare, dal documento che mi ha inviato Andy, le tante formule elaborate con Latex, la trasformazione di parti del testo in immagini è stato l'unico espediente che ho trovato per pubblicare l'articolo senza dover chiedere a Andy di riscrivere tutto (e purtroppo non è possibile eliminare le cornici dalle immagini). Se qualcuno di voi sapesse come fare, per favore lo scriva nei commenti oppure a infinitoteatrocosmo@gmail.com. Grazie!

                    

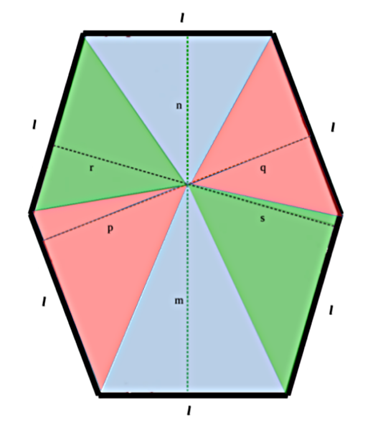
Dato un esagono di lato l con i lati tutti uguali tra loro e quelli opposti paralleli, si tracciano tre altezze (di misure differenti) congiungenti i lati opposti che si possono denominare: h₁ , h₂ , h₃ .

Scelto un punto interno dell’esagono in maniera tale che per lo stesso transitano le tre altezze, queste vengono divise rispettivamente nei segmenti:  m, n,   p, q,     r, s.

Si può allora scrivere:

             m + n = h₁

            p  + q = h₂

            r  + s = h₃

 e sommando

             m + n + p + q + r + s = h₁ + h₂ + h₃

L’area dell’esagono sarà quindi pari alla somma delle aree dei 2 triangoli azzurri più i 2 triangoli rosa più i 2 triangoli verdi:

Si consideri adesso lo stesso esagono di figura 1, ma con costruzioni aggiuntive, come in figura 2:

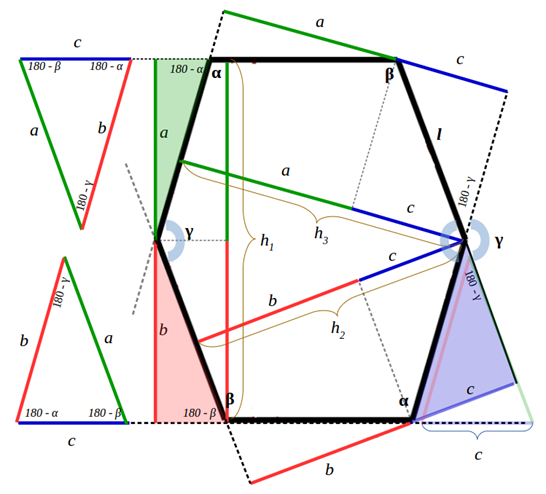
qui le tre altezze dell’esagono ,  e vengono divise nei segmenti  da tratti di linea perpendicolari alle altezze stesse e che si dipartono da vertici opposti (i segmenti tratteggiati interni di figura 2), ovvero facendo scorrere le altezze lungo prolungamenti dei lati paralleli dell’esagono sino a intercettare un vertice opposto.

 

 

 

 

Osservando sempre la figura 2, gli angoli interni opposti dell’esagono sono uguali perché angoli alterni di rette parallele (in questo caso segmenti paralleli) tagliate da una trasversale; per lo stesso criterio saranno uguali anche quegli esterni supplementari.

Costruendo successivamente un triangolo ausiliario esterno avente per lati i segmenti a, b, c e posizionandolo in basso a sinistra con la base c sovrapposta sul prolungamento del lato “sud” dell’esagono e con il lato a parallelo al lato di “sud-ovest” dell’esagono, si nota come l’angolo alla base in basso a destra (180-β) è uguale all’esterno supplementare di β (perché angoli corrispondenti di segmenti paralleli tagliati da una trasversale).

Ruotando lo stesso triangolo lungo il suo asse verticale, capovolgendolo e posizionandolo in alto a sinistra con la base c sovrapposta sul prolungamento del lato “nord” dell’esagono, con il lato b parallelo al lato di “nord-ovest” dell’esagono, si nota come l’angolo alla base in alto a destra (180-α) è uguale all’esterno supplementare di α (perché angoli corrispondenti di segmenti paralleli tagliati da una trasversale).

Così come l’angolo (180 - γ) corrisponde all’angolo al vertice del triangolo ausiliario posto in basso a destra in forma semitrasparente, con la base c sovrapposta sul prolungamento del lato “sud” dell’esagono e il lato a sovrapposto sul prolungamento del lato “nord-est” dell’esagono.

Applicando adesso il teorema dei seni al triangolo ausiliario esterno all’esagono, si può scrivere:

e sostituendo:

Ma si era dimostrato all’inizio che:

L’area dell’esagono così calcolata è in funzione di porzioni delle sue altezze; ma se si volesse esprimere in funzione direttamente delle altezze, è necessario effettuare dei passaggi aggiuntivi.

Osservando figura 2 (che riproponiamo per comodità del lettore), si considerino adesso delle semplici somme e sottrazioni tra le altezze h₁ , h₂ , h₃:

 

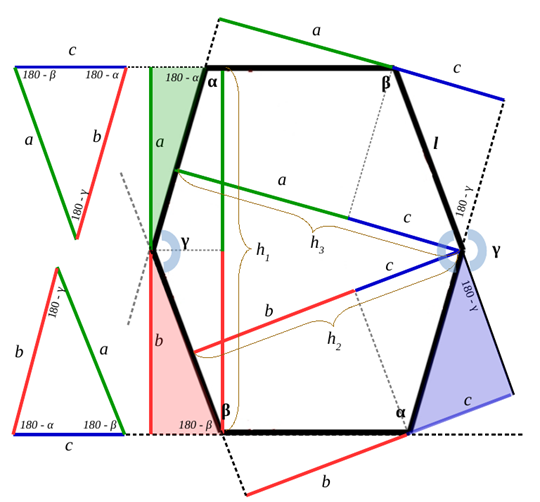
mentre l’area del triangolo ausiliario di lati a, b, c si può ricavare con la formula di Erone: