Categorie: Matematica
Tags: cubo formiche geometria parallelepipedo quiz zucchero
Scritto da: Vincenzo Zappalà
Commenti:24
La corsa allo zucchero **
Due formiche (F e F') si trovano di fronte a due pietre dalla forma di solidi geometrici perfetti. F ha davanti a sé un cubo di spigolo uguale a 3 e F' un parallelepipedo rettangolo di spigoli uguali a 3, 2 e 4, come mostrato nella figura che segue.
Nei vertici più lontani da loro, in A e A', sopra le pietre, vi sono due succulente zollette di zucchero. Le formiche corrono con la stessa identica velocità e possono, ovviamente, salire anche le pareti verticali.
Se F parte da P e F' parte da P', chi delle due arriverà per prima alla sua zolletta posta nei vertici A e A', rispettivamente?
Ovviamente, bisogna anche dimostrarlo.
QUI la soluzione
24 commenti
arrivano uguali infatti il percorso piu' breve e' l'ipotenusa di un triangolo base 3 ed altezza 6
Supposta furbina la f' direi lei, perché![\sqrt[2]{18} > 4](http://latex.codecogs.com/gif.latex?\sqrt[2]{18}&space;>&space;4)
.
O c'è sotto qualcosa di più?
Già, ha ragione Silvano...
è facile ... ma non così tanto. Indicatemi anche bene i percorsi...
Basta sviluppare i due parallelepipedi sul piano. Nel caso del cubo si deve percorrere la diagonale formata da un rettangolo formato da due quadrati adiacenti quindi la radice quadrata di 45 (62 + 32 )
nel secondo caso ho due percorsi uno (3+4)2 + 22 = 53 e l’altro (2+4)2 + 32=45.il secondo è più conveniente ed è uguale alla lunghezza del percorso del cubo
Ernesto
Mi pare che la formica alle prese con la pietra cubica sia costretta a percorre in ogni caso, come percorso di minore lunghezza, quello lungo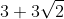
(cioè circa 7,242). Nel caso della pietra parallelepipeda, invece, io riesco a trovare un percorso lungo 7: da P' salgo in verticale lungo lo spigolo (lungo 2) , poi procedo lungo la diagonale della faccia superiore fino ad A' (lunga 5). La lunghezza totale del percorso è 2+5=7. Per cui, se sceglie questo percorso, la formica F' arriva prima.
Ho ipotizzato, pero', che le formiche dovessero muoversi solo passando dai vertici. In effetti nulla vieta alle formiche di passare tra due vertici attraversando lo spigolo che li unisce. In tal caso vale quanto gia' scritto da Ernesto.
La formica F potrebbe salire sulla faccia verticale in linea retta, salendo di x mentre va a destra di 3, per poi proseguire in linea retta sull'altra faccia, salendo ancora di 3-x. Applicando il teorema di Pitagora, la lunghezza totale del percorso sarebbe
y=√(3²+x²)+√[3²+(3-x)²]=√(9+x²)+√(x²-6x+18)
con 0≤x≤3
Derivando la funzione e facendo il confronto tra le ordinate si può determinare il minimo della funzione, ovvero la lunghezza del percorso minimo per la prima formica.
Analogamente si può procedere per la seconda formica, con la complicazione di dover scegliere 2 facce su 3.
(è tardi, per ora mi fermo qui)
Ah, per simmetria mi aspetto che il percorso minimo per la prima formica si ottenga a metà (x=3/2).
Insomma... non era così facile! Niente equazioni, mi raccomando... non sarebbe "elegante"
Risolvendo il problema di massimo e di minimo si trova che il percorso minimo è quello del cubo indicato al mio messaggio precedente. La lunghezza risulta
d=√[3²+(3/2)²]+√[3²+(3-3/2)²]=2√[3²+(3/2)²]=2√(9+9/4)=6√[1+1/4]=6√5/2=3√5≈6,7082
Per un qualunque parallelepipedo diverso dal cubo, mi risulta che il percorso minimo corrisponda a percorrere uno spigolo, seguito dalla diagonale della faccia successiva.
Siccome ho dovuto risolvere l'equazione d'=0, mi fermo qui.
Se mi dai il permesso, pubblico anche i calcoli.
Sicuramente per il parallelepipedo ho sbagliato qualcosa, non torna.
caro Marco... non mi stupisco...
Ho cambiato idea, voto per la soluzione di Ernesto:
Parallelepipedo:
√[(2+3)²+4²]=√(25+16)=√41 (sinistra+sopra)
√[(2+4)²+3²]=√(36+9)=√45 (davanti+sopra) *
√[(3+4)²+2²]=√(49+4)=√53 (davanti+destra)
Cubo:
√[(3+3)²+3²]=√(36+9)=√45 (sinistra+sopra) *
Arrivano insieme.
Volevo dire, prima il parallelepipedo (√41)
Pardon per la fretta...
Riassumendo quanto già scritto prima dagli altri lettori, ho proiettato su piano la parete di fronte alle formiche e il “tetto” delle figure geometriche solide:
=> 
=> 
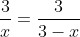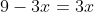
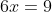
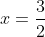
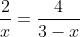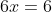
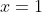
Per similitudine tra i triangoli rettangoli opposti ad un vertice aventi per ipotenusa il tratto rosso e il tratto verde, si può scrivere
per il cubo:
per il parallelepipedo:
Siccome il percorso minimo è dato da una somma di segmenti consecutivi adiacenti, esprimendolo in funzione di x si può scrivere&space;=&space;\sqrt{x^2&space;+&space;9}&space;+&space;\sqrt{(3&space;-&space;x)^2&space;+&space;9})
&space;=&space;\sqrt{x^2&space;+&space;4}&space;+&space;\sqrt{(3&space;-&space;x)^2&space;+&space;16})
&space;=&space;3\sqrt{5})
&space;=&space;3\sqrt{5})
ovvero &space;=&space;g(1)&space;=&space;\sqrt{3^2&space;+&space;6^2}&space;=&space;\sqrt{45}&space;=&space;3\sqrt{5})
per il cubo:
per il parallelepipedo:
e sostituendo i valori di x trovati si avrà:
Ma la formica F' è più furbacchiona e decide di percorrere un tragitto differente rispetto all'amica F:
=> 
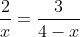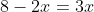
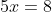
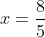
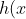&space;=&space;\sqrt{x^2&space;+&space;4}&space;+&space;\sqrt{(4&space;-&space;x)^2&space;+&space;9})
&space;=&space;\sqrt{41})
mentre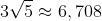 
quindi F' percorrendo questo tragitto, dovrebbe impiegare un tempo minore rispetto a F.
Sempre per similitudine tra i triangoli rettangoli aventi per ipotenusa il tratto rosso e il tratto verde, si può scrivere:
In questo caso l'equazione in funzione di x del percorso minimo è:
Ora
Insomma, ragazzi, basta portarsi in Flatlandia... e ricordare che lo spazio rimane euclideo... (pochi calcoli e ...)
Beh, visto che ormai la soluzione è stata pubblicata, mi permetto di pubblicare la versione con utilizzo dell'analisi per determinare il percorso più breve tra i vertici opposti di un parallelepipedo.
Sicuramente mooolto più elaborata (mi piace rendere complicate le cose semplici :twisted:)
d(x)=√(a²+x²)+√[b²+(c-x)²]=√(a²+x²)+√(x²-2cx+b²+c²)
0≤x≤c
d'(x)=(2x)/[2√(a²+x²)]+(2x-2c)/[2√(x²-2cx+b²+c²)]=x/√(a²+x²)+(x-c)/√(x²-2cx+b²+c²)
d'(x)≥0
x/√(a²+x²)≥(c-x)/√(x²-2cx+b²+c²)
m.c.m (moltiplichiamo per quantità positive, non cambia verso)
x√(x²-2cx+b²+c²)≥(c-x)√(a²+x²)
Eleviamo al quadrato (i due membri sono positivi o nulli a causa delle limitazioni del problema):
x²(x²-2cx+b²+c²)≥(c²-2cx+x²)(a²+x²)
x⁴-2cx³+b²x²+c²x²≥a²c²+c²x²-2a²cx-2cx³+a²x²+x⁴
Semplifichiamo:
b²x²≥a²c²-2a²cx+a²x²
(b²-a²)x²+2a²cx-a²c²≥0
Primo caso: a≠b
Equazione associata:
x={-a²c±√[a⁴c²+a²c²(b²-a²)]}/(b²-a²)={-a²c±√[a⁴c²+a²b²c²-a⁴c²]}/(b²-a²)={-a²c±√[a²b²c²]}/(b²-a²)=(-a²c±abc)/(b²-a²)=(a²c∓abc)/(a²-b²)=ac(a±b)/[(a-b)(a+b)]
x₁=ac(a-b)/[(a-b)(a+b)]=ac/(a+b)
x₂=ac(a+b)/[(a-b)(a+b)]=ac/(a-b)
Se a<b, a²<b², e quindi b²-a²>0. Quindi la disequazione è verificata per valori esterni all'intervallo tra le due radici, ovvero (essendo a<b, e quindi ac/(a-b)<0),
x≤ac/(a-b) ∨ x≥ac/(a+b)
Se, al contrario, a>b, a²>b², e quindi b²-a²<0. Quindi la disequazione è verificata per valori interni all'intervallo tra le due radici.
Poiché in questo caso e ac/(a+b)<ac/(a-b) (ac/(a-b)>0, quindi, a parità di numeratore positivo è puù piccola la frazione con denominatore positivo più grande), la soluzione è
ac/(a+b)≤x≤ac/(a-b)
Verifichiamo se 0≤x₁≤c.
Sicuramente ac/(a+b)>0; inoltre, se fosse ac/(a+b)>c, sarebbe anche a/(a+b)>1, da cui (a+b)/a<1, 1+b/a<1 e b/a<0, il che è impossibile.
Quindi x₁ è accettabile.
Verifichiamo se 0≤x₂≤c.
x₂ non è accettabile per a<b (altrimenti x₂<0). Quindi limitiamoci al caso a>b.
Se fosse x₂≤c, ac/(a-b)≤c ⇒ a/(a-b)≤1, da cui, passando agli inversi,
(a-b)/a≥1 ⇒ 1-b/a≥1 ⇒ -b/a≥<0 ⇒ b/a≤0
Ma questo è impossibile, quindi x₂ non è accettabile.
L'unico valore che annulla la derivata è x=ac/(a+b); inoltre, sia per a<b che per a>b la derivata è negativa alla sua sinistra e positiva alla sua destra. Di conseguenza per x=ac/(a+b) la funzione ha un minimo relativo, che è anche (essendo l'unico), quello assoluto.
Secondo caso: a=b
(a²-a²)x²+2a²cx-a²c²≥0
2a²cx-a²c²≥0
2x-c≥0
x≥c/2
Anche in questo caso la derivata si annulla per x=c/2, è positiva alla sua destra e negativa alla sua sinistra, e quindi la funzione ha un minimo reltativo (e assoluto) per x=c/2.
A questo punto basta dare ad a, b e c i valori possibili, cercando il valore più piccolo di d.
Beh... Marco ci sei riuscito egregiamente! E poi dicono che la matematica non è divertente!!!
Insomma, Enzone, non ti resta che ufficializzare la soluzione così potrò inserirla qui http://www.infinitoteatrodelcosmo.it/ce-percorso-percorso/
Hai perfettamente ragione Scherzy... ma aspettiamo almeno domani. Magari qualcuno vuole ancora provarci senza leggere i commenti... Ha avuto un sacco di lettori in un solo giorno: sarà il lockdown??
Caro Enzo, penso ci siano diversi modi per risolvere questo problema.
Io ne ho scelto uno che parte dal fatto che la formica può muoversi sia in verticale che in orizzontale.
Pertanto posso trasformare lo zucchero in tre dimensioni (solido) in una figura geometrica a due dimensioni, collegando la faccia frontale a quella superiore dello zucchero, in modo da notare immediatamente qual è il percorso più breve, ossia la diagonale del rettangolo risultante.
Giusto per confermare che quello è il percorso più breve basta tracciare un cerchio con al centro (P o P') e la cui circonferenza interseca l'angolo superiore del rettangolo così costruito a cui la formica deve arrivare (A o A').
Ovviamente la diagonale del rettangolo così costruito corrisponde al raggio del cerchio, ossia alla distanza centro circonferenza del cerchio.
Così facendo, applicando il teorema di Pitagora ottengo il valore del percorso minimo, ossia il valore della diagonale del rettangolo che corrisponde anche il raggio del cerchio.
La figura mostra cosa si ottiene per per lo zucchero a forma di cubo:
La seconda figura cosa si ottiene con lo zucchero a forma di parallelepipedo:
Come si può notare il percorso più breve è identico per le due formiche che se si muovono alla medesima velocità impiegano lo stesso tempo.
Vabbè speriamo di non aver detto qualche sciocchezza!
Paolo
La strategia è giusta, Paolino, ma ...
Ma... non ho pensato ad usare la faccia laterale del parallelepipedo e quella superiore, ottenendo così un rettangolo di lati 4 e 5 (2+3), per cui r = √4² + (2 +3) ²= √4² + 5²= 6,403.
Ciò significa che la formica del parallelepipedo compie un tragitto più breve a e quindi arriva prima.
Ovviamente questa soluzione non vale, poiché dopo aver postato la mia ho visto le figure di Andy e mi sono reso conto dell'errore.
Bravo Andy ed bravo anche Marco che ci è arrivato seguendo un altra strada.
Paolo