Riproponiamo, diviso in sei puntate, un articolo che deve rappresentare l'ABC per chi volge lo sguardo al cielo: una semplice spiegazione di come funziona quella stupefacente macchina del tempo che l'Universo mette a disposizione di chiunque abbia occhi e testa (e un pizzico di buona volontà!) per comprenderla ed ammirarla. In questa sesta (e ultima) puntata approfondiamo ulteriormente il problema della distanza tra due oggetti cosmici.

QUI le altre puntate  -  QUI l'articolo intero (pubblicato il 10/1/2018)

 

Distanze e velocità della luce: Universo in espansione ** 

Attenzione, però, che ciò è possibile se i fotoni che hanno lasciato la stella hanno potuto viaggiare senza alcun intoppo. Infatti, se il tempo necessario alla luce per coprire una certa distanza fosse di 57 anni, ma essa si fermasse a fare uno “spuntino” da qualche parte per una ventina d’anni per poi riprendere il viaggio, la nostra misura finale di 77 anni sarebbe errata, a meno di non venire a conoscenza della sosta e quindi di potere tenerne conto sottraendola al valore finale.

Purtroppo, i fotoni non parlano e non ci diranno mai se sono fermati da qualche parte o quantomeno se hanno rallentato. In realtà i fotoni non rallentano e nemmeno si fermano a mangiare (al limite si affievoliscono). La loro velocità è costante e teoricamente senza intoppi. Ma è lo spazio che devono percorrere che può giocare loro degli scherzi, quando il gioco si fa duro, ossia quando il tempo impiegato dalla luce è veramente MOLTO lungo. L’espansione dell’Universo non può più essere trascurata e, anzi, è proprio lei che determina il tipo di distanza che possiamo ottenere.

Se esso si “ingrandisse” notevolmente, i fotoni dovrebbero percorrere una distanza maggiore di quella preventivata. La misura della distanza, espressa in anni luce, avrebbe un significato diverso. Ci direbbe soltanto che la luce è partita al tempo t1, ossia un certo numero di anni fa, e ci ha raggiunto OGGI, ma non ci darebbe una misura corretta della distanza reale della stella al tempo t1, né di quella di OGGI. In altre parole, il numero di anni impiegati dalla luce a percorrere lo spazio tra la stella e noi poco avrebbe in comune con la vera distanza tra la galassia e noi. La situazione, quando si parla di distanze veramente grandi è, però, proprio questa ed è in perfetta sintonia con quanto visto nei capitoli precedenti.

Per riassumere, potremmo dire che le distanze misurate, senza intoppi da parte dei fotoni, sono quelle relative a uno spazio che può essere considerato immutabile, in cui gli oggetti si muovono soltanto per il loro moto proprio. Qualcosa di molto simile alle distanze misurate nella realtà di tutti i giorni. Se invece lo spazio non è immutabile, ma cambia costantemente, le distanze assumono significati diversi e più complessi.

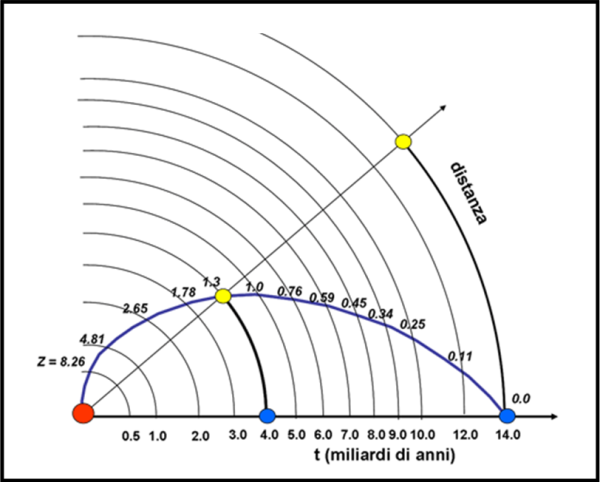
Purtroppo, per distanze veramente grandi, maggiori di un paio di miliardi di anni luce, lo spazio non può approssimarsi come immobile, o meglio statico. Esso si espande continuamente e il percorso della luce compiuta in un certo periodo di tempo è ben maggiore di quello relativo alla differenza di tempo tra quando i fotoni sono stati emessi e OGGI. In altre parole, dire che una galassia è vecchia di 10 miliardi di anni è ancora esatto, ma dire che essa dista 10 miliardi anni luce da noi NON è più esatto. A questo punto dobbiamo farci aiutare dalla Fig. 19 (che ormai conosciamo abbastanza bene), in grado di sintetizzare e chiarire quanto detto finora e permettere di definire le distanze in uno spazio in espansione.

Come già sappiamo, lo spazio è considerato a una dimensione ed è rappresentato dalle conferenze concentriche che si allargano sempre più a causa dell’espansione dell’Universo. Il tempo scorre invece in senso radiale. La posizione della Terra è rappresentata dalla sferetta blu e l’asse orizzontale descrive il nostro tempo (NON è una posizione privilegiata, dato che qualsiasi retta che parta dal Big Bang può essere considerata asse delle ascisse). Lo spazio invece varia da momento a momento e le distanze possono essere misurate solo su queste circonferenze.

Se non ci fosse espansione e potessimo bloccare lo spazio (ad esempio quello relativo a 4 miliardi di anni dopo il Big Bang), tutte le misure di distanza, se possibili, sarebbero senza ambiguità e si ricondurrebbero ai metodi accennati precedentemente. Purtroppo (o per fortuna?) lo spazio, invece, si espande.

Sappiamo anche che la linea curva, che parte dal Big Bang e giunge fino a noi, rappresenta il CONO DI LUCE relativo al nostro passato, ossia tutto ciò che noi riusciamo a vedere oggi. Per il momento tralasciamo i numeri scritti vicino al CONO DI LUCE: ci torneremo tra poco.

Se non ci fosse espansione, la luce ci raggiungerebbe senza “intoppi” e la distanza tra la galassia e noi sarebbe uguale all’arco di cerchio marrone tra le sferette gialla e blu. Potrebbe essere espressa correttamente in anni luce, ossia in spazio percorso dalla luce per andare dalla sferetta gialla a quella blu. Purtroppo, però, mentre la luce tenta di descrivere il tratto marrone, lo spazio si è espanso e dopo un miliardo di anni è diventato una circonferenza con un raggio maggiore. La luce è costretta, quindi, a viaggiare anche in senso radiale rispetto al Big Bang. Come conseguenza il suo moto sarà spaziotemporale, dato che lo spazio dipende direttamente dal tempo a causa dell’espansione.

Qual è allora la vera distanza percorsa dalla luce? Non è ovvio rispondere, come potete facilmente vedere. La traiettoria descritta è spaziotemporale, ma la distanza deve essere misurata nello spazio (ossia, lungo una circonferenza). Sì, ma quale? Quello di 4 miliardi di anni dopo il Big Bang (arco nero) o quello di oggi (arco viola)? Entrambe sono giuste, ma differiscono di molti anni luce tra loro. Forse sarebbe meglio usare un valore medio? No, no, sarebbe comunque sbagliato.

Molto meglio, allora, calcolare entrambe le distanze e chiamarle per nome, in funzione del tempo: d_E, al momento t = 4 miliardi di anni dopo il Big Bang, quando la luce è stata emessa (arco marrone) e d_A, al momento t = 14 miliardi di anni, ossia quella attuale. Esse sono distanze reali, misurabili in anni luce, ma estremamente diverse tra loro, a causa dell’espansione.

Tuttavia, le relazioni esistenti tra queste distanze, in funzione del tempo e del tipo di espansione prescelto, possono essere calcolate.

La distanza di una galassia espressa in anni luce non ha più  senso. OGGI la galassia gialla disterà da noi più dei 10 miliardi di anni, cui generalmente ci si riferisce quando si danno i risultati di oggetti ultra lontani. Dire, ad esempio, che la radiazione cosmica di fondo dista da noi poco meno di 14 miliardi di anni (o che lo stesso Big Bang dista 14 miliardi di anni) è in realtà un errore. E’ invece giusto dire che la sua età è di 14 miliardi di anni o meglio che la luce emessa (e che oggi ci raggiunge) è partita 14 miliardi di anni fa. Un errore comunissimo, veniale se vogliamo, ma che spesso getta grande confusione nella comprensione dello spazio-tempo. Ovviamente, i professionisti sanno benissimo a cosa ci si riferisce e come trasformare quel dato in distanze reali. Ma per i non addetti ai lavori, la cosa può dare luogo ad ambiguità.

Vale la pena ricordare come si determinano le distanze di oggetti, lontanissimi nel tempo, attraverso la legge di Hubble. Essa, in modo molto semplice, dice che esiste una relazione tra la velocità di espansione dell’Universo (o meglio ancora di allontanamento tra le galassie) e distanza dell’oggetto celeste. La relazione è lineare e vale semplicemente d = Ho ∙ v, dove d è la distanza, v è la velocità di allontanamento e Ho è una costante. Tuttavia, Ho è una costante variabile, in quanto assume valori sempre diversi in tempi diversi (rappresenta in pratica le modalità dell’espansione).

Essa è una costante per un tempo ben determinato, nel senso che è uguale per tutto l’Universo all’istante t. Ne consegue che essa fornisce un valore diverso della distanza a seconda del tempo e quindi della costante che noi inseriamo. Questo fatto ci porta a una conclusione importantissima. Il valore più importante è quello realmente osservato della velocità di allontanamento, ottenuto attraverso il redshift z (spostamento delle righe spettrali verso il rosso). A partire da questa velocità è possibile, attraverso formule più o meno complicate, calcolare le distanza che preferiamo. E’ giusto quindi inserire sul CONO DI LUCE i valori del redshift z per i vari tempi a partire dal Big Bang, come fatto in Fig. 19. Ricordiamo brevemente che il redshift si misura direttamente guardando di quanto una certa riga dello spettro elettromagnatico si è spostata verso il rosso (lunghezza d'onda più lunga) rispetto a ciò che si osserva in laboratorio.

Essi ci forniscono le velocità che sono strettamente legate alle distanze che vogliamo considerare. La formula (banale) che lega le distanze prima definite e il redshift è la seguente: d_E= d_A/ ( 1 + z ). Ne segue che 1/(1 + z) è un vero e proprio fattore di riduzione che ci permette di risalire alle vere distanze al momento dell’emissione della luce, in funzione del redshift osservato. Ovviamente, il suo inverso (1 + z) permette di passare dalla distanza di emissione a quella attuale ed è il fattore di espansione dell’Universo.

Essendo il valore di z legato strettamente al tempo di emissione, esso si usa per stabilire l’età dell’emissione della luce da parte dell’oggetto (concetto esatto) o la distanza in anni luce (non esatta, ma facilmente riconducibile alle distanze reali). Questa situazione porta, però, a incomprensioni. Si dice, ad esempio, che il Big Bang ha un’età di circa 14 miliardi di anni (esatto), ma si dice anche che esso dista 14 miliardi di anni luce (errato). E’ invece vero che l’Universo Osservabile ha un raggio di circa 47 miliardi di anni luce. Com’è possibile che vi siano oggetti più distanti del Big Bang? Tutto torna perfettamente se teniamo conto di quanto ho cercato di esprimere precedentemente (spero, almeno…).

Come già accennato, per oggetti più vicini di circa un paio di miliardi di anni (temporalmente), i problemi sollevati possono essere “praticamente” trascurati, in quanto l’espansione non ha causato grandi differenze (il più delle volte nei limiti della precisione delle misure).

A questo punto, possiamo concludere descrivendo le distanze principali che si usano nell’Universo e la loro definizione. Esse sono quattro:

1) Distanza comovente (d_C). Essa indica la distanza che si espande con l’Universo. In altre parole, essa dice dove si trovano le varie galassie OGGI, anche se la luce era partita da loro quando l’Universo era ben più piccolo e le distanze minori. Essa è uguale alla nostra d_A. Con questa definizione l’Universo osservabile ha un raggio pari a 47 miliardi di anni luce, mentre le galassie più lontane visibili con il telescopio Spaziale Hubble hanno una distanza di circa 32 miliardi di anni luce (questa differenza vuole solo dire che non abbiamo ancora osservato con Hubble TUTTO l'Universo osservabile: la luce è arrivata, ma era troppo debole per lo strumento). La distanza comovente può anche essere considerata una costante in un sistema di riferimento che tenga conto intrinsecamente del fattore di espansione (1 + z), dato che la sua variazione dipende solo da tale fattore.

2) Distanza di diametro angolare (d_A). Noi vediamo oggi le galassie com’erano al momento in cui ci hanno inviato la luce. In quel momento sappiamo benissimo che la distanza (d_E) era minore di quella che è oggi. Le dimensioni della galassia che vediamo oggi sono relative, però, a quel ben determinato istante. In altre parole, le dimensioni della galassia sono ben più grandi di quanto ci si aspetterebbe da un oggetto così lontano. In altre parole ancora, il diametro angolare di una galassia si conserva attraverso l’espansione (l’espansione espande lo spazio, non i singoli oggetti). Ne consegue che il diametro angolare che vediamo oggi è strettamente legato alla distanza della galassia al momento dell’emissione della luce (d_E). Questo tipo di distanza è in pratica la distanza al momento dell’emissione della luce.

3) Distanza di luminosità (d_L). Durante l’espansione, la luce che arriva fino a noi è molto più debole di quanto indicherebbe la distanza che la galassia aveva al momento dell’emissione della luce. Ciò è causato dalla dispersione della luce su una superficie più vasta. Ne consegue che le galassie più lontane osservate dal telescopio Spaziale appaiono come se si trovassero a distanze di circa 350 miliardi di anni luce. Ovviamente essa non è una misura realistica, ma è utile per determinare il fattore di affievolimento della luce.

4) Distanza di tempo luce (d_T). Essa rappresenta il tempo impiegato dalla luce di una galassia per giungere fino a noi. Questa definizione è quella che ci permette di dire che il Big Bang è “distante” circa 14 miliardi di anni luce. Essa è però, in realtà, una misura di tempo e non di distanza. In pratica si ottiene semplicemente moltiplicando l’età di un evento per la velocità della luce.

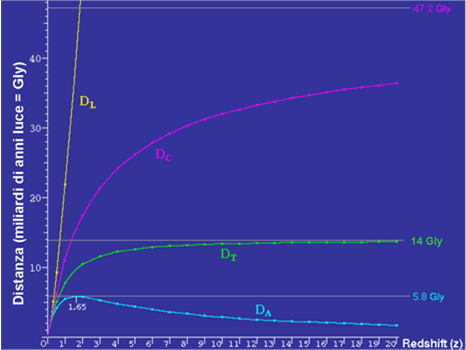
L’andamento di queste quattro distanze in funzione del redshift z è riportato in Fig. 20. Per come sono state definite è abbastanza ovvio che per oggetti relativamente vicini a noi (redshift minori di 0.1) e relativamente vicini nel tempo (un paio di miliardi di anni) le quattro distanza coincidono tra loro.

 

A questo punto siamo pronti per avvicinarci all'ultima frontiera dell'Universo... quella oltre la quale, nonostante i progressi tecnologici, sarà molto probabilmente impossibile guardare con altri occhi che non siano quelli della mente: la sfera di Hubble.

 

QUI le altre puntate  -  QUI l'articolo intero (pubblicato il 10/1/2018)