Questo articolo è stato inserito in "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo" e "Matematica e Geometria"

 

I giapponesi, oltre a tutti i loro misteri, i loro riti, le loro cerimonie, il loro modo di pensare e agire, ben diverso da quello occidentale, ci hanno anche regalato una geometria del tutto speciale, veramente affascinante. Iniziamo a entrare in questo mondo, dove intendo tornare spesso...

Tra il 1603 e il 1868, l'epoca dei samurai, il Giappone si chiude in se stesso, estraniandosi completamente dalle culture straniere. La matematica e la geometria non erano mai state affrontate con particolare attenzione e riflettevano quel poco che proveniva dalla Cina attraverso la Corea. Tuttavia, proprio nel periodo Edo, quello sopra citato, vi è una fioritura eccezionale dell'economia, dei rapporti sociali e della cultura, in genere. I giapponesi scoprono i misteri della matematica e della geometria, utilizzando approcci del tutto personali. Nasce così la geometria dei templi. A tutti i livelli di istruzione, vengono proposti, affrontati e, spesso, risolti particolari problemi che vedono frequentemente protagonisti cerchi e tangenze varie tra di essi.

Ne proporremo qualcuno anche noi, ma, come antipasto, vediamo un metodo tutto giapponese per disegnare un pentagono regolare. Spesso i problemi hanno risvolti che toccano l'architettura, ma il più delle volte sono problemi puramente mentali che hanno un seguito incredibile tra la popolazione. Viene chiamata geometria dei templi, dato che i vari quesiti geometrici vengono dipinti su tavole e queste esposte nei templi, come una specie dei nostri ex voto. Ma, in questo caso, il loro significato è ben diverso: stimolare alla soluzione o riportarla attraverso dimostrazioni, spesso del tutto sconosciute agli occidentali. Queste tavolette prendono il nome di Sangaku e rappresentano una visione del tutto peculiare, veramente affascinante.

Un pentagono alla giapponese

La costruzione si avvale solo di circonferenze e ci porterà alla immancabile serie di Fibonacci...

Consideriamo una circonferenza, di raggio unitario e centro O, e tracciamo due diametri ortogonali tra loro, come mostra la Fig. 1.

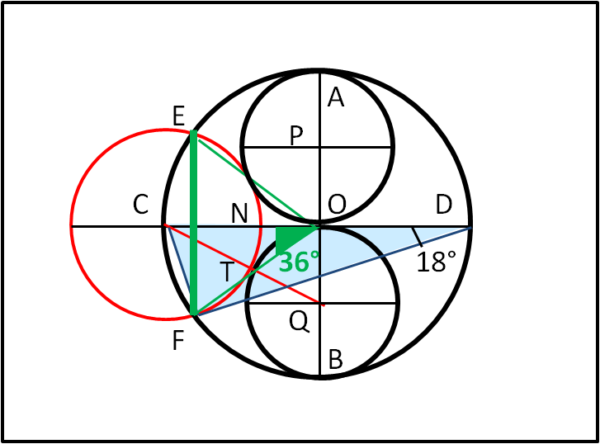
Nella stessa figura tracciamo due circonferenze, aventi i loro centri lungo il diametro verticale, tale che sino tangenti tra loro e con la circonferenza di partenza. Ne segue che esse sono uguali e hanno come raggio la metà del raggio del cerchio di base. Siano P e Q i loro centri.

Uniamo  Q con il punto C, intersezione della circonferenza più grande con il diametro orizzontale e indichiamo con T il punto appartenente alla circonferenza di centro Q posto lungo la congiungente CQ. Facendo centro in C, disegniamo la circonferenza di raggio uguale a CT. Quest'ultima interseca la circonferenza iniziale nei punti E ed F. Bene... questi due punti appartengono al pentagono regolare iscritto nella circonferenza di raggio unitario. In altre parole, il segmento EF è proprio il lato del pentagono.

Dimostriamolo facilmente, ricordando che il raggio (OA = OC) della prima circonferenza è uguale a 1.

La distanza CQ vale:

CQ = √(CO² + OQ²) = √(1 + 1/4) = √5/2

Per costruzione:

CE = CF = CT = CQ - QT = √5/2 - 1/2 = (√5 - 1)/2

Consideriamo il triangolo CFD. Esso è rettangolo in F, dato che quest'angolo è l'angolo alla  circonferenza di un semicerchio.

Possiamo perciò scrivere che:

sen(CDF) = CF/CD = ((√5 - 1)/2)/2 = (√5 - 1)/4

CDF vale, perciò, esattamente 18°.

Dato che COF è l'angolo al centro relativo all'arco CF, ed è quindi doppio dell'angolo alla circonferenza CDF, è ovvio che

COF = 36°

Da cui:

EOF = 72°,

72° è proprio l'angolo che sottende il lato di un pentagono regolare: EF è il lato richiesto!

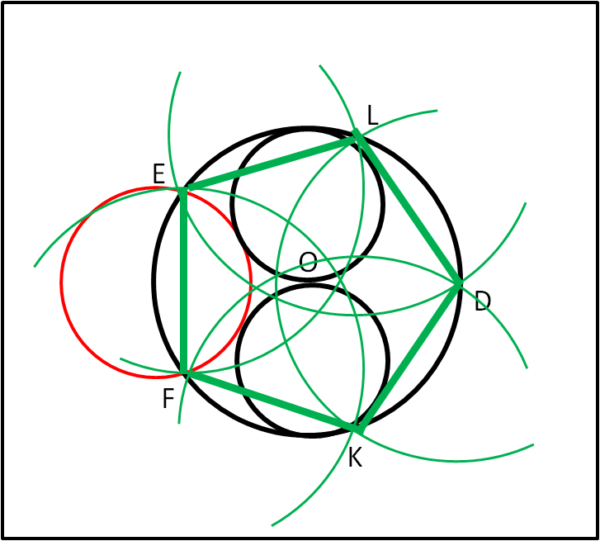
Basta, ora, fare centro in E e tracciare la circonferenza di raggio EF, determinando immediatamente un altro vertice del pentagono (L) e via dicendo fino a tornare in F (Fig. 2), con un favoloso intreccio di curve (alla giapponese, appunto...).

Non possiamo, però, fermarci qui... Avrete notato sicuramente che compare la radice quadrata di 5, un numero che ci ricorda la celebre sezione aurea  e, quindi, la serie di Fibonacci . Vuoi vedere che ci ricadiamo?

Tracciamo una nuova circonferenza di raggio OR, come mostrato in Fig.3.

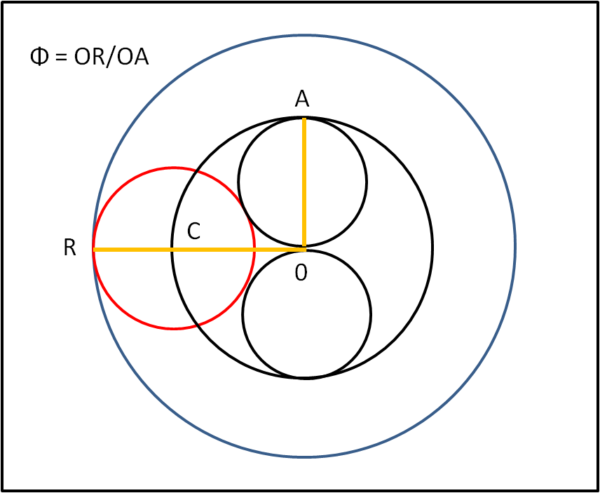
Quanto vale OR?

(Ricordando che CR = CN = CF)

OR = OC + CR = 1 + CN = 1 + CF = 1 + (√5 - 1)/2 = (1 + √5)/2

Ne segue che il rapporto tra OR e OC ( = OA = 1) è proprio la sezione aurea ∅:

∅ = OR/OA = (1 + √5)/2

Alla prossima...

Sayonara (さようなら)