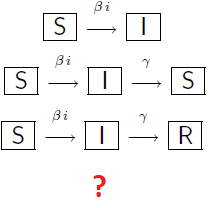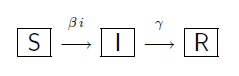Questo articolo contiene una panoramica dei tre modelli matematici trattati, applicabili ad eventi che riguardano "cose" che si trasmettono con il contatto tra individui di una popolazione. N.B.: per i dettagli , vi rimando al tag modelli matematici dove trovate per esteso tutti i calcoli. Sostanzialmente , tutto si basa principalmente sulla formula, giustificata sia statisticamente che empiricamente: […]
Non bastava Erone a regalarci triangoli con i lati e le aree intere, si ci è messo anche quel genio incontrastato che è stato Eulero, prospettandoci un supermattone! Un bravissimo a Maurizio che ha risolto il quesito da par suo.
Il tempo profondo fa parte del patrimonio cognitivo umano ma non è sempre stato così. E' una conquista recente che trova ugualmente grandi difficoltà a radicare nella mente umana per via delle sua caratteristiche dimensionali lontane dalla quotidianità, al pari dei grandi temi descrittivi dell'universo
La sonda BepiColombo, così chiamata in onore del grande Bepi, maestro insuperabile di Meccanica Celeste da cui tutti noi abbiamo imparato quasi tutto e al quale l'Italia aveva tolto la cattedra di Padova perché giudicata poco interessante, costringendolo ad andarsene in America e vedersi offrire cattedre nelle più prestigiose Università degli Stati Uniti, benchè ancora ben lonatna da Mercurio (sua meta finale) ci invia immagini bellissime.
Una delle analogie più usate (ma anche, spesso, fraintesa) per capire l'espansione dell'Universo è quella del palloncino che si gonfia. Ma, a volte, i VERI palloncini possono avere dei difetti o non essere perfettamente sferici...
Parlare di barche, navi e della loro stabilità sia con mare calmo che agitato comporterebbe un intero libro (e magari nemmeno basterebbe). Tuttavia, dato che, comunque, una nave galleggia per effetto del Teorema di Archimede non possiamo esimerci dal dare qualche informazione di base a riguardo.
Spesso e volentieri cerchiamo di unire cultura generale e cultura scientifica, ben sapendo che esiste, in fondo, una e una sola cultura, sempre condita di un sano pizzico di ironia, verso se stessi e gli altri. Approfittando di una celebre serie di racconti della fine del 1300, all'inizio del ventesimo secolo vennero creati una serie di puzzle, in qualche modo legati a quelle storie medioevali. Presentiamone uno, sperando che possa far passare il tempo a grandi e piccini in questo periodo di clausura forzata.
Stiamo forse per fare la loro stessa sorte? Magari non per un asteroide, ma per qualcosa di molto più piccolo? Probabilmente no, ma se l'uomo non imparerà a diventare umile e rispettoso verso la Natura, potrebbe anche darsi che la prossima volta sarà così.
Questo articolo è più di un quiz... è un invito a scrivere un romanzo o addirittura stendere la sceneggiatura per un film di fantascienza. Tutto parte dal monolito di 2001: Odissea nello Spazio.
Almeno tre segnali stanno facendo perdere la speranza di poter vedere una cometa luminosa come Venere se non di più. Purtroppo è questa una sorte abbastanza normale per chi osa passare troppo vicino al Sole (ed è fatto di ghiaccio sporco...). Tuttavia, se deve trasformarsi in polvere planetaria, che lo faccia fare anche al nostro poco piacevole amico virus...
Purtroppo ancora un articolo tecnico; del resto per affrontare a grandi linee la dimostrazione della congettura, abbiamo bisogno di alcuni concetti di geometria differenziale. In questo articolo cominciamo ad affrontare la curvatura di una linea. E' l'esempio più facile di curvatura di una varietà; il caso n=1. La curvatura di una linea, ci servirà poi per analizzare la curvatura di una superficie, per poi astrarci al caso più generico di varietà di dimensione qualsiasi (il tensore di curvatura d Riemann).
Nel processo di riqualificazione che abbiamo descritto nel precedente articolo, sul modello SIS, si ipotizzava che la popolazione totale restasse costante. La somma delle due percentuali, Istruiti e Superati, valeva quindi costantemente 1. Introduciamo una nuova ipotesi che tenga conto di un fenomeno di “abbandono”. Vale a dire che, tra tutti coloro che periodicamente rientreranno nel circolo della […]
Approfondiamo l'argomento della stabilità dell'equilibrio che abbiamo trattato parlando del galleggiamento nell'ambito del teorema (o "principio") di Archimede, riproponendo un articolo che qualche anno fa abbiamo proposto sotto forma di quiz.
Il titolo è alquanto sibillino, ma vuol dire, in pratica, che se ci accorgiamo che la Natura rompe quella che noi consideravamo una perfetta simmetria, è molto facile che il modello da noi costruito sia sbagliato.
Ogni promessa è un debito; questa appendice vuole giustificare (con il metodo rigoroso dell'analisi) le equazioni differenziali comparse nello studio dei modelli SIS e SI. Mi dispiace, dovevo farlo prima.
Come detto, questa serie di articoli vuole essere veramente divulgativa e adatta a qualsiasi livello, sempre che si abbia già un'infarinatura dei concetti di limite, derivata e integrale. Per ottenere ciò, penso che non mi picchierete se a volte sarò ripetitivo e quasi banale. Nella versione definitiva, si potrà sempre cercare di compattare meglio la materia e renderla più uniforme. Per adesso pensiamo ad affrontare nel modo più chiaro possibile i concetti fondamentali.