Un problema di semplice geometria che non è di risoluzione proprio immediata...

Un quiz abbastanza istruttivo che necessita riflessione e concentrazione.  I tre asterischi sono relativi all'intuizione e non certo alla difficoltà matematica e/o geometrica. Come sempre, ci sono sicuramente vari modi per risolverlo, ma un premio speciale di niente a chi trova il più "elegante".

Ambientiamolo nell'antico Giappone.

Un ricco possidente terriero vuole fare un regalo a un suo dipendente sempre estremamente zelante e laborioso. Tuttavia, vuole anche mettere alla prova le sue capacità di ragionamento, in vista di una possibile promozione.

Lo chiama e lo porta con sé in uno splendido campo di grano dalla forma perfettamente uguale a un triangolo equilatero.

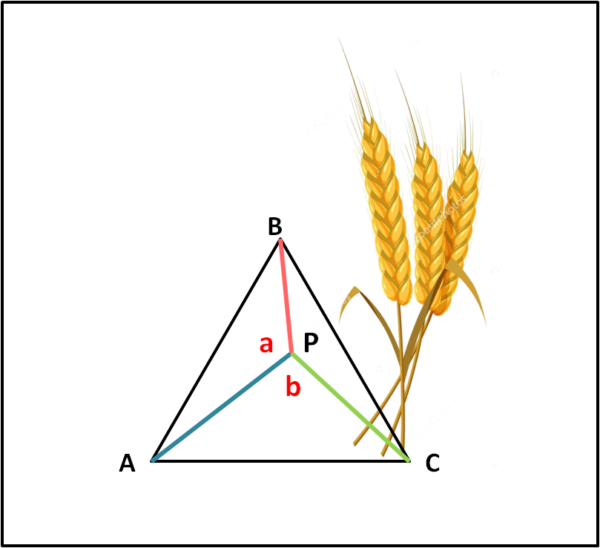
Invita il dipendente a scegliere un punto qualsiasi interno al campo e di segnarlo con un bastone. Eseguita questa operazione, gli permette di misurare la distanza esatta del punto dai tre vertici del triangolo (PA, PB, PC). Gli permette anche di misurare due angoli (a e b) compresi tra queste direzioni, come riportato nella figura che segue.

A questo punto, porge al dipendente un foglio e una matita e gli promette di regalargli una parte di terreno uguale all'area di un triangolo che abbia per lati le tre distanza misurate. L'unica condizione è che il dipendente sappia dirgli, senza effettuare altre misure, l'ampiezza dei tre angoli del triangolo così costruito.

Vogliamo aiutarlo?

QUI la soluzione