Eccovi la soluzione del quiz, perfettamente individuata da Fabrizio, prima, e da Gianfranco dopo. Per non parlare di Leandro che ha perfino introdotto un aiuto di tipo "fisico" per aiutare il nostro fratello scansafatiche. Tuttavia, non si pretendeva tanto e quindi limitiamoci alla soluzione puramente "matematica".

Come vi dicevo, il quiz diventa molto facile se si pensa subito ad assegnare ad ogni interruttore e, di conseguenza, ad ogni lampada, un codice binario. Basterebbe dire che con questa numerazione sono sufficienti sette combinazioni diverse di 0 e di 1 per scrivere i primi 128 numeri. Noi  abbiamo solo 100 interruttori e, quindi, sette viaggi sono più che sufficienti.

Fatte queste premesse, non è difficile trovare un  metodo che permetta ad ogni viaggio di inserire un nuovo indice al codice che si sta costruendo. In binario bastano  4 cifre per indicare i primi 10 numeri (basterebbero anche per i primi 16 numeri, da 0 a 15). In realtà, il numero di cifre aumenta di una per ogni multiplo di 2. Così due cifre sono sufficienti fino a 4, tre cifre fino a 8, quattro fino a 16, cinque fino a 32, sei fino a 64, SETTE fino a 128. Se avessimo avuto 1000 interruttori ce la potevamo cavare con 10 viaggi soltanto.  Per semplificare, descriviamo il caso in cui vi siano solo 10 interruttori, ma la strategia può continuare in modo simile fino al numero che si vuole...

La prima cosa da fare è accendere tutte le luci del castello, ossia mettere il loro interruttore locale su ON. A questo punto si fa il primo viaggio nella centralina e si mettono su ON 5 interruttori e 5 su OFF. Su quelli messi su ON si scrive  1 (acceso) e su quelli messi su OFF si scrive 0. Si torna nel castello e si fa la stessa cosa sugli interruttori locali (o vicino ad essi). Se la luce è rimasta accesa si scrive 1, se si è spenta si scrive 0.

A questo punto si effettua il secondo viaggio alla centralina. Abbiamo di fronte 5 ON e 5 OFF. Dividiamo ogni gruppo a metà o, dato che 5 è dispari, in 2 e 3 (poco importa).  I primi 5 erano tutti zero? Bene, ne mettiamo 2 su ON e 3 li lasciamo su OFF. Aggiungiamo la cifra 1 su quelli che abbiamo acceso e inseriamo un altro o su quelli che sono rimasti spenti. In tal modo abbiamo due interruttori con il codice 01 e tre con il codice 00.

Passiamo poi ai 5 che erano stati messi su ON (ossia, avevano già la prima cifra uguale a 1). Facciamo una cosa analoga a quella fatta col  primo gruppo di 5 (quelli spenti in origine): ne spostiamo due su OFF e tre li lasciamo su ON. Ne segue che i primi due avranno il codice 10 e gli altri tre 11. Non ci resta che tornare al castello e scrivere  1 per le luci accese e 0 per le luci spente. In tal modo riproduciamo perfettamente quanto è stato segnato nella centralina.

Siamo pronti per il terzo viaggio. Del primo gruppo di due interruttori accesi (con codice 01) ne mettiamo uno su OFF e uno lo lasciamo acceso: essi diventano 010 e 011. Poi abbiamo di fronte i tre interruttori che avevano codice 00. Bene, i primi due li accendiamo e aggiungiamo 1 (011) e il terzo lo lasciamo com'è, inserendo un  altro 0 (000). Una operazione analoga la facciamo per i due indicati da 01: uno lo spegniamo e diventa o1o e l'altro lo lasciamo com'è e diventa 100. Infine abbiamo di fronte i tre interruttori che erano indicati con 11. I primi li spegniamo e diventano 110, mentre l'ultimo lo lasciamo com'è e diventa 111. Torniamo al catello e aggiungiamo i codici 1 se sono accesi e 0 se sono spenti.

Ed eccoci al quarto e ultimo viaggio alla centralina. I primi due li possiamo lasciare com'erano, aggiungendo 0 per chi era spento e 1 per chi era acceso, ottenendo così  0100 e 0111. Poi abbiamo i due accesi col codice 001 e ne cambiamo uno solo ottenendo 0010 e 0011. Poi troviamo lo 000 e possiamo benissimo accenderlo ottenendo 0001. Procedimento analogo per i rimanenti in modo da avere, alla fine, 4 cifre per ogni interruttore. I codici sono tutti diversi tra loro e individuano perfettamente in modo univoco i 10 interruttori centrali.

Ci siamo anche accorti che potevamo  lasciarne qualcuno ancora spento e qualcuno ancora acceso o cose del genere dato che con quattro cifre eravamo in grado di identificare perfettamente non solo dieci interruttori, bensì 16 (compreso lo o). A questo punto, se vogliamo compattare il codice possiamo trasformarlo  in numero decimale. Abbiamo, ovviamente, tutti numeri diversi con qualche "buco", dato che abbiamo considerato solo 10 dei primi 16 numeri, includendo anche lo zero.

Non ci resta che tornare al castello e completare il codice mettendo 1 sulle luci accese e 0 su quelle spente. Anche per loro si può eseguire la trasformazione in numeri decimali e il gioco è fatto!

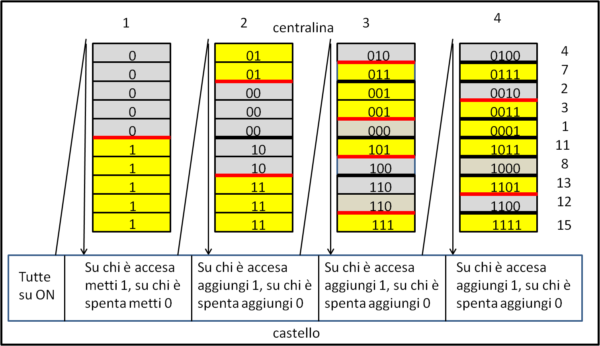
La figura che segue mostra in grafico quanto detto a parole...

In fondo, i calcolatori agiscono così...

QUI trovate il quiz