Questo articolo è stato inserito nelle sezioni d'archivio "Geometria dello spazio" e "Astronomia classica"

In questo articolo descrivo la realizzazione di un  modello di geometria solida con il quale ho voluto verificare il funzionamento di una montatura equatoriale, ossia un particolare sostegno di un telescopio molto utilizzato in ambito amatoriale e non solo. La montatura equatoriale  consente  con un unico movimento, manuale o motorizzato, di "inseguire" il moto apparente di un astro nel cielo, in realtà ruotando in sincrono col moto di rotazione terrestre.

E’ noto che il moto apparente degli oggetti astronomici che osserviamo in una notte stellata è in realtà dovuto alla rotazione della Terra attorno al proprio asse. La stella a noi più vicina, il Sole, appare ad un osservatore posto in un dato punto della superficie terrestre sorgere ad est, percorrere la volta celeste da est verso ovest e poi tramontare ad ovest, fino a scomparire sotto l’orizzonte dell’osservatore. Nella realtà è la Terra che  ruota attorno al proprio asse, con una velocità angolare di 15° / ora, così da completare un giro completo nell’arco di 24 ore (24x15°=360°). Tutto ciò che osserviamo in cielo appare solcare la volta celeste in virtù della rotazione della Terra attorno al proprio asse.

Chi desidera cimentarsi con l’osservazione astronomica , anche a livello amatoriale, deve inevitabilmente imbattersi, prima o poi, nella necessità di “inseguire” l’oggetto astronomico osservato. Quest’ultimo, infatti, qualora il telescopio fosse tenuto fermo verso la direzione in cui l’oggetto è stato inquadrato, uscirebbe ben presto fuori dall’obiettivo dello strumento. Questo sarebbe un problema che , se non risolto, impedirebbe, tra l’altro, l’uso di tecniche di ripresa di lunga durata, necessarie ove si vogliano fotografare  oggetti astronomici del profondo cielo, molto  deboli e lontani (nebulose e galassie).

Si deve, quindi, agire in qualche modo sull’orientamento del telescopio. E’ per tale fine che vengono utilizzate diverse tipologie di montature, ossia sistemi meccanici di supporto e movimentazione di telescopi, in genere motorizzati ma nulla vieta che siano solo manuali.

Le montature altazimutali , come dice il loro stesso nome, ruotano il telescopio secondo due direzioni, una sul piano azimutale, parallelo all’orizzonte, e una su quello verticale, perpendicolare all’orizzonte, come illustrato nella seguente figura.

Con tale tipo di montature, l’inseguimento dell’oggetto inquadrato richiede un aggiornamento continuo di entrambi gli angoli di rotazione (quello azimutale e quello relativo all’ altezza sull’orizzonte). La circostanza è agevolmente visibile nella seguente animazione.

Le montature equatoriali sono, invece, caratterizzate dal fatto che, una volta puntato l'oggetto da osservare, esso viene inseguito mediante la rotazione del telescopio attorno ad un solo asse.

Ma prima di addentraci nella comprensione del loro funzionamento, è necessario ricordare alcuni parametri astronomici e introdurre il sistema equatoriale di coordinate astronomiche. A tale fine, si faccia riferimento alla seguente figura.

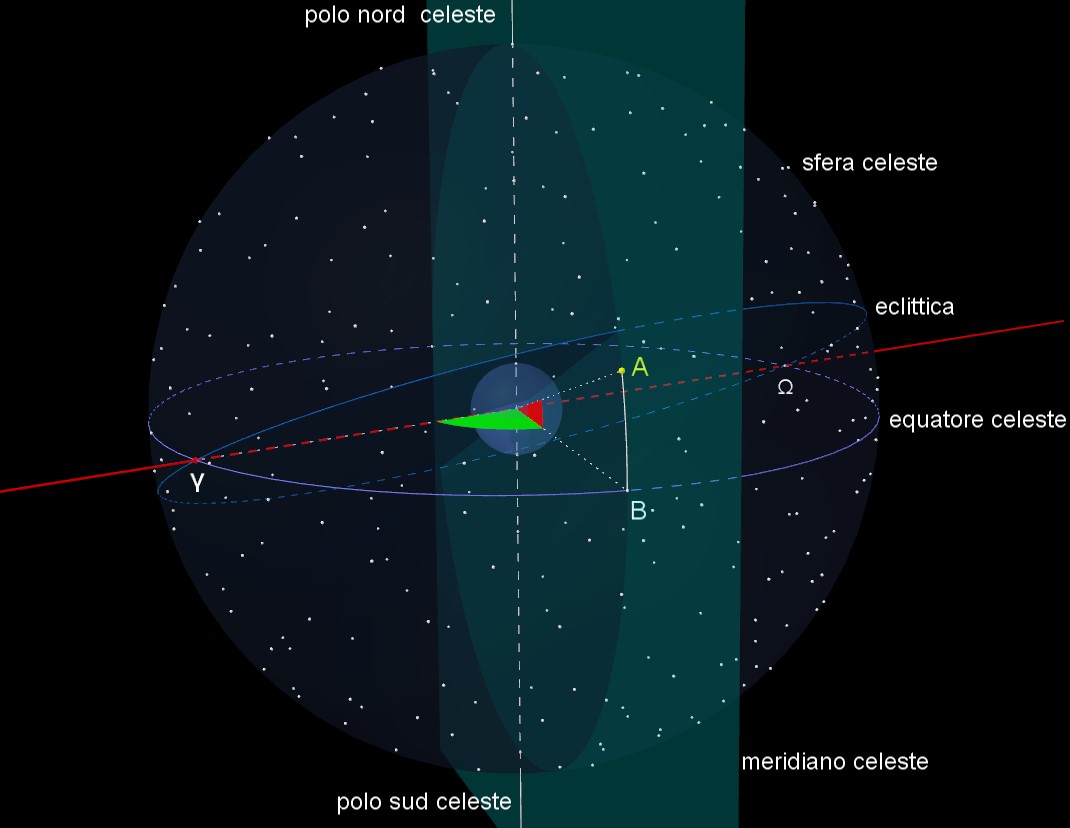
Si definisce sfera celeste una sfera immaginaria, concentrica alla Terra e di raggio arbitrario, sulla quale si proiettano gli astri. Sezionando tale sfera con il piano dell’equatore terrestre, si ottiene il corrispondente equatore celeste. Sezionando , invece, la sfera celeste con il piano contenente l’orbita terrestre attorno al Sole , si ottiene l’eclittica. Le suddette due circonferenza (equatore celeste ed eclittica) si intersecano in due punti, indicati con γ e Ω e chiamati, rispettivamente, punto di Ariete e punto della Bilancia. Nel punto di Ariete, detto anche punto vernale, il Sole, nel suo moto apparente per chi lo osserva da Terra, passa nel momento dell’equinozio di primavera boreale. Nel punto della Bilancia, invece, il Sole passa nel momento dell’equinozio autunnale boreale. Il punto vernale viene scelto come origine nel sistema di coordinate equatoriale.  In particolare, un generico astro A, colorato in giallo nella precedente figura, è univocamente individuato in tale sistema di coordinate equatoriali, mediante due angoli: l’ascensione retta (AR) e la declinazione (DEC).

N.B.: per maggiori approfondimenti sui vari sistemi di coordinate e sulla geometria sferica in generale, vedi QUI e soprattutto QUI.

L’angolo di ascensione retta è quello colorato in verde nella figura. In pratica è l’angolo, misurato sul piano dell’equatore celeste, compreso tra il punto di Ariete e il punto di intersezione tra l’equatore celeste e il punto B, intersezione tra il meridiano celeste e l’equatore celeste. L'ascensione retta si misura in ore, da 0 a 24. Volendo usare i gradi, va semplicemente osservato che un angolo giro di ascensione retta, cioè 24 ore, corrispondono a 360°. Per cui ogni ora di ascensione retta corrisponde a 15°.

L’angolo di declinazione è quello colorato in rosso nella figura. Esso è l’angolo, misurato nel piano del meridiano celeste, compreso tra il punto B e la congiungente l’astro A con il centro della Terra. La declinazione si misura direttamente in gradi e può variare da -90° a +90°.

E' da notare la caratteristica fondamentale di queste coordinate e cioè che entrambe, ascensione retta e declinazione, sono legate unicamente alla sfera celeste, poiché  è su di essa che vengono presi tutti i riferimenti per misurarle. Grazie a questo fatto, le coordinate equatoriali di un astro, essendo indipendenti dal moto di rotazione terrestre, non cambiano col tempo. A meno che non si tenga conto del particolare movimento "a trottola" dell'asse di rotazione terrestre, il cui orientamento spaziale cambia continuamente col tempo. Questo fa si che anche l'inclinazione del piano dell'equatore celeste cambi nel tempo, facendo variare di conseguenza le coordinate equatoriali di un astro. Tale movimento dell'asse terrestre, detto di precessione, avviene tuttavia in tempi molto lunghi. Un giro di precessione completo dell'asse terrestre impiega, infatti, circa 25772 anni terrestri per compiersi. Su tempi ragionevolmente limitati, definiti epoche,  se ne può trascurare l'effetto sulla posizione degli astri sulla sfera celeste, avendo però cura di precisare l'epoca a cui si riferiscono le coordinate ed eventualmente applicare dei coefficienti correttivi per riportarle alla data corrente.

Una volta note le coordinate equatoriali di un astro, volendolo osservare da un punto della superficie terrestre, che ruota attorno al proprio asse nell'arco della giornata,  sarà, ovviamente, necessario inseguirlo, movimentando il telescopio utilizzato, in modi differenti a seconda del tipo di montatura utilizzata. Nel caso della montatura altazimutale, come accennato sopra, sarà necessario correggere costantemente l'angolo azimutale e quello d'altezza. Nel caso delle montature equatoriali, invece, si è detto che è sufficiente movimentare il telescopio solo secondo una direzione. E' giunto il momento di capire perché e come ciò è possibile.

Vediamo prima come è fatta una montatura equatoriale.

Essa è dotata di due assi, attorno ai quali è possibile la rotazione, motorizzata o manuale: l’asse polare (o dell’ascensione retta) e l’asse della declinazione, tra loro perpendicolari. L’asse polare , come suggerisce il suo stesso nome, va orientato nella direzione della stella polare (Polaris). La stella polare, come noto, è prossima al polo nord celeste, ossia all’intersezione tra sfera celeste e l'asse di rotazione della Terra. Questo fa si che, osservandola, risulti praticamente immobile in cielo, contrariamente alle altre stelle. E’ anche vero che questa sua caratteristica non è eterna. Tra circa 13700 anni, infatti, non sarà più la stella polare a indicarci il polo Nord celeste ma la stella Vega. Siamo tuttavia ancora ben lontani da allora, per cui la stella polare resta il nostro riferimento. Come si fa ad orientare l’asse dell’ascensione retta verso la stella polare ? Innanzitutto si orienta l’asse verso il Nord. Poi lo si inclina, rispetto al piano orizzontale su cui è ubicata la montatura, di un angolo esattamente uguale alla latitudine del posto. Si faccia riferimento alla seguente figura.

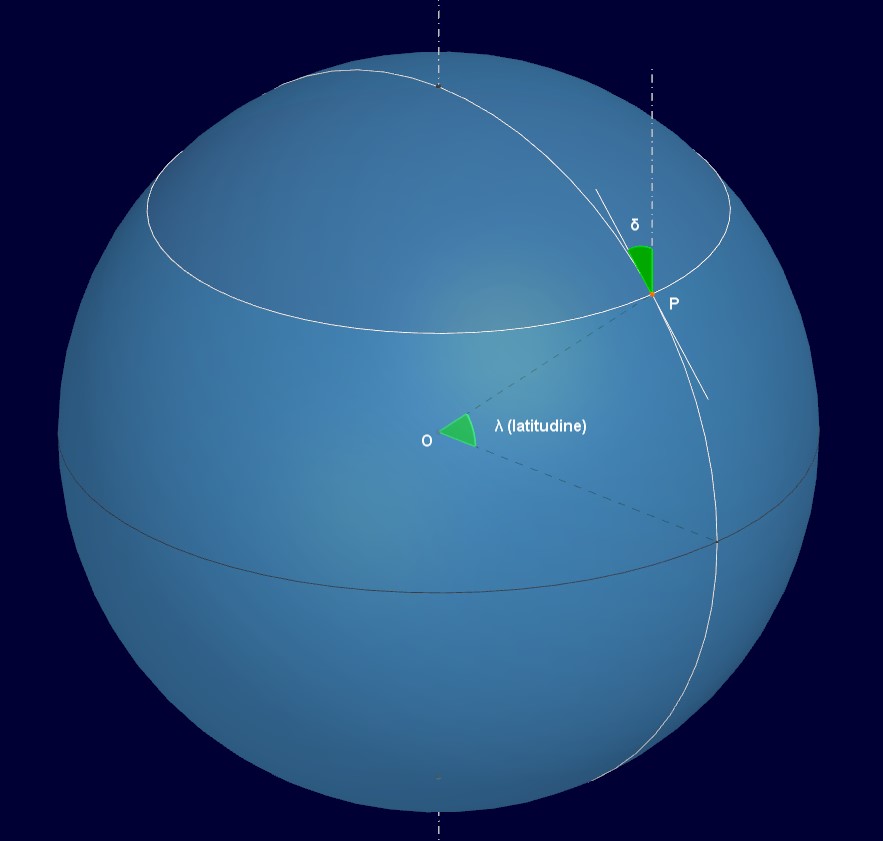
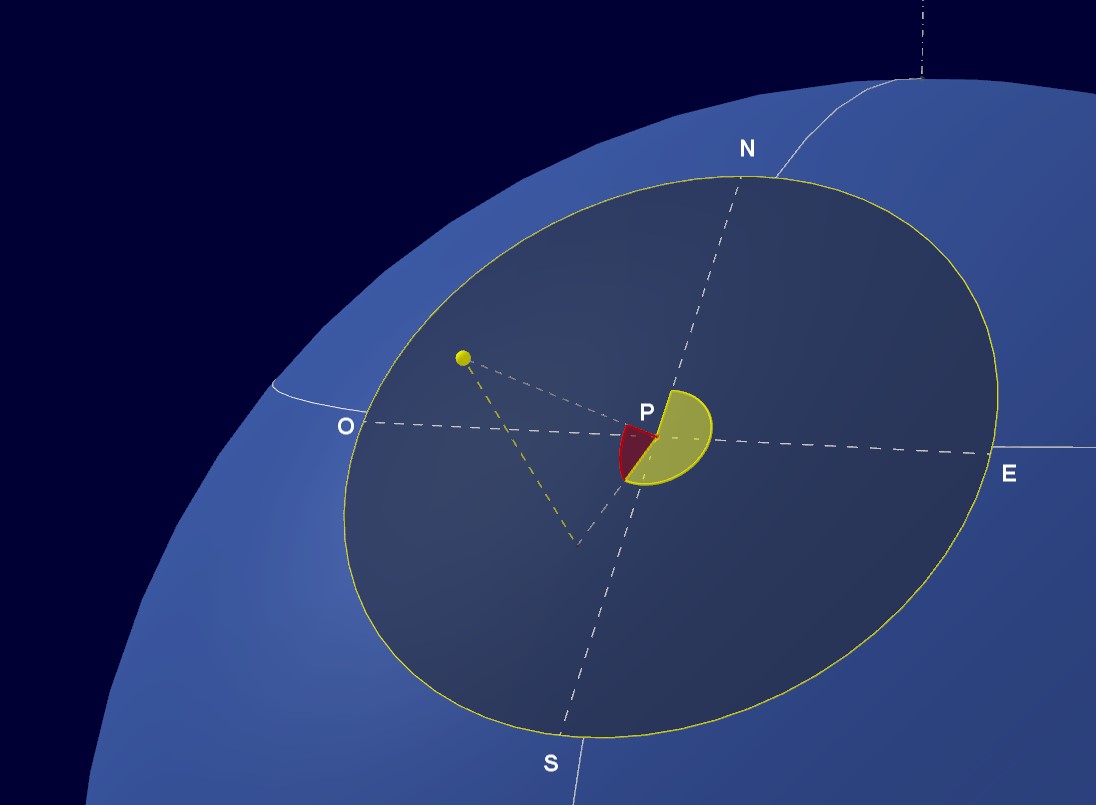
P è il punto della superficie terrestre in cui si trova l’osservatore con la sua montatura equatoriale. Le circonferenze bianche sono il parallelo e il meridiano passanti per il punto P. La semiretta tratteggiata bianca che si diparte da P rappresenta l’asse polare della montatura. L’angolo  è quello di inclinazione dell’asse polare rispetto alla tangente in P al meridiano del luogo. L’angolo , invece, è la latitudine del luogo.

Portiamoci  ora sul piano cui appartiene il meridiano di P.

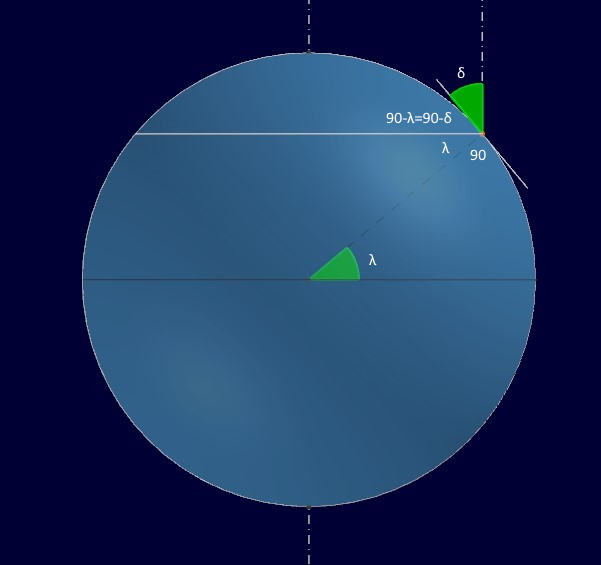
Dalla figura è evidente che i due angoli e non possono che essere tra loro congruenti perché complementari di uno stesso angolo. Puntando la montatura a Nord e inclinando l’asse polare della montatura equatoriale di un angolo pari alla latitudine del luogo, esso risulta, dunque, orientato verso la stella polare e parallelo a quello di rotazione terrestre.

Ora ci si propone di verificare che , una volta orientato correttamente l'asse polare della montatura equatoriale, per inseguire il moto apparente di un astro nella volta celeste è sufficiente ruotare il telescopio solo attorno al suddetto asse polare.

Ho realizzato, allo scopo, un modello di geometria solida con l'app Geogebra. Quella che segue è un' immagine di tale modello.

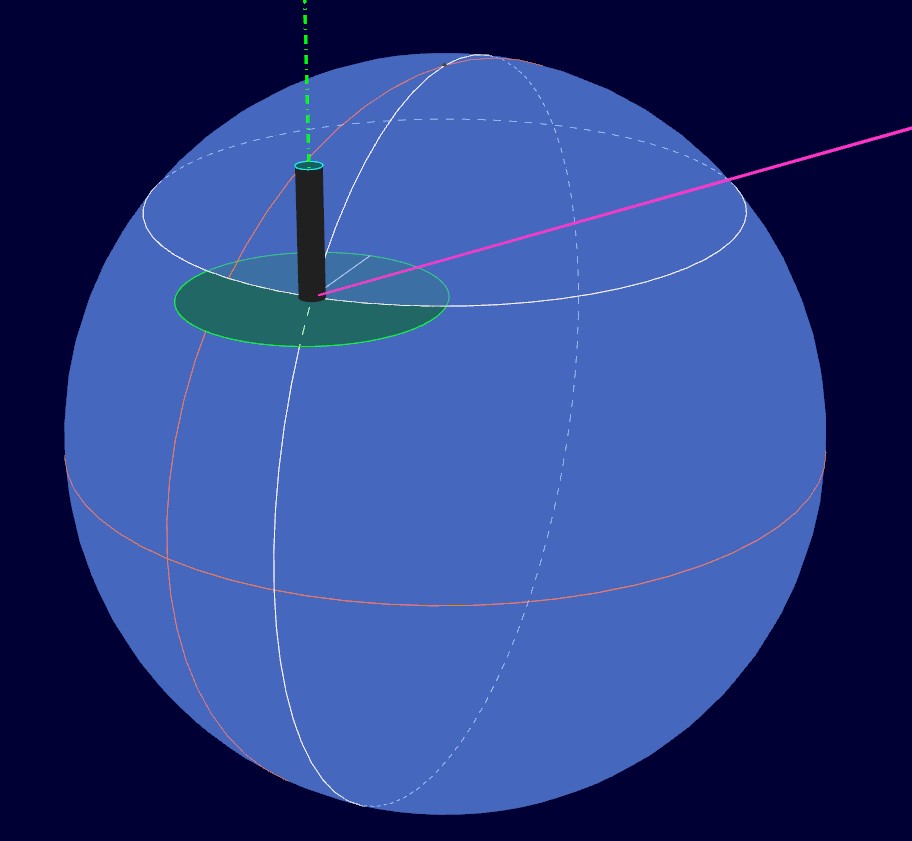
La sfera celeste è la Terra. I due cerchi massimi arancioni sono l'equatore e il meridiano di Greenwich. I due cerchi bianchi sono il parallelo e il meridiano del punto di osservazione terrestre. Il cilindretto nero rappresenta il telescopio, ovviamente non in scala. La semiretta color fucsia è la linea di mira verso l'astro oggetto di osservazione, posizionato sulla sfera celeste, non visibile per chi guarda l'immagine suddetta. La semiretta a tratto e punto di colore verde è l'asse polare della montatura. Il cerchio minore di colore verde è perpendicolare all'asse polare della montatura. Il telescopio, in questa immagine, si trova nella sua posizione di "parcheggio", ossia con l'asse ottico parallelo a quello polare.

Nel modello geometrico ho utilizzato come unità di misura delle lunghezze le migliaia di chilometri. Quindi, ho dato alla sfera rappresentante la Terra un raggio di 6,37 unità , mentre alla sfera celeste un raggio di 150000 unità. In questo modo, un oggetto rappresentato sulla sfera celeste del mio modello geometrico è come se si trovasse alla distanza fisica dal centro della Terra di 150.000.000 chilometri (pari a circa 1 unità astronomica, ossia la distanza media Terra-Sole). In pratica, ho dato al modello una scala geometrica così da poter rappresentare la situazione reale nello spazio ristretto  del monitor di un computer..

Ora si punti il telescopio verso l'astro che si vuole osservare. La seguente animazione illustra l'operazione.

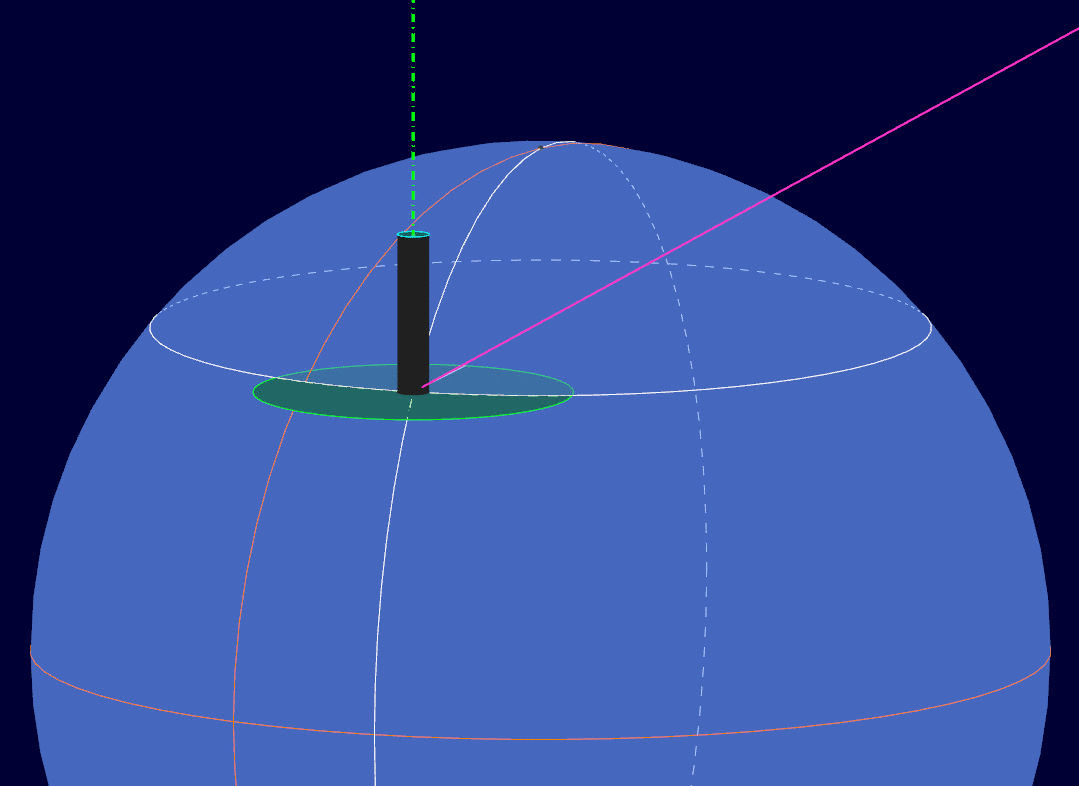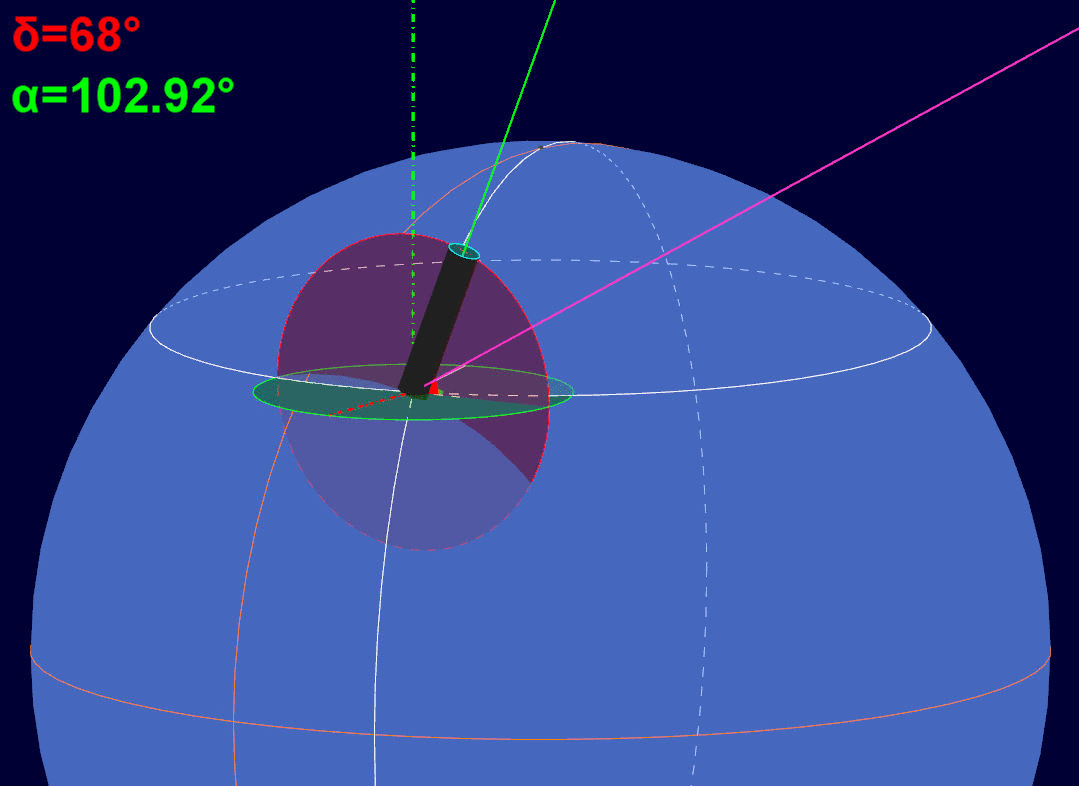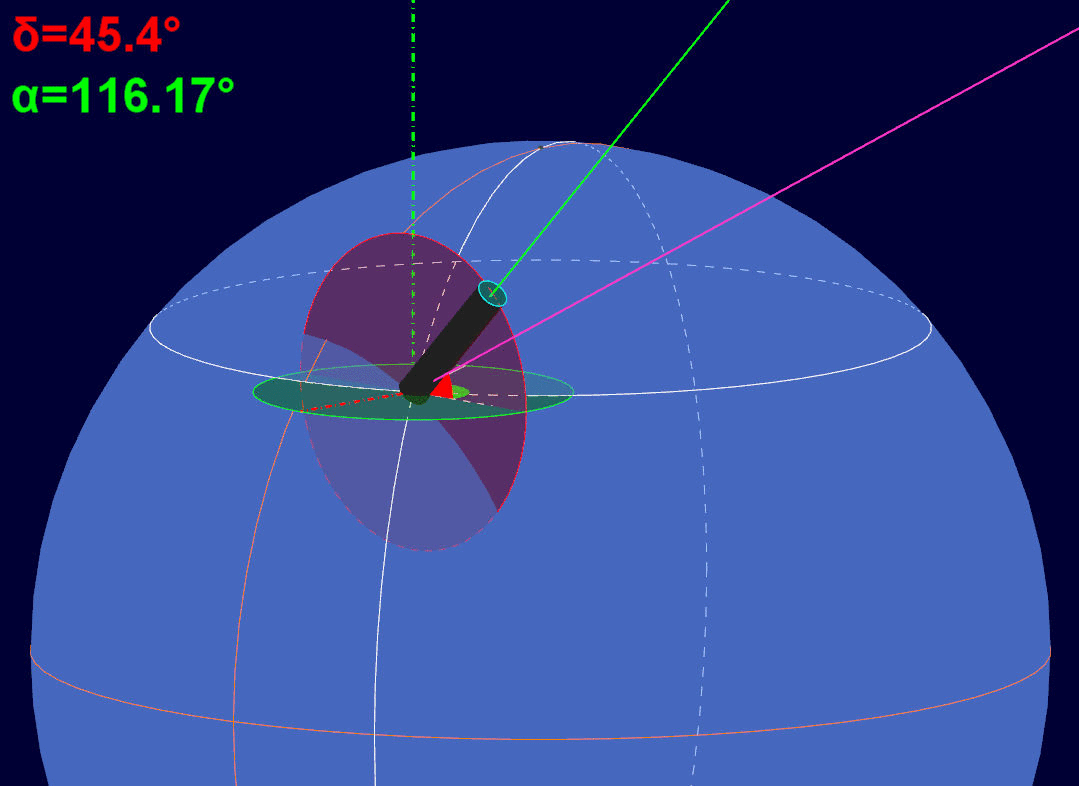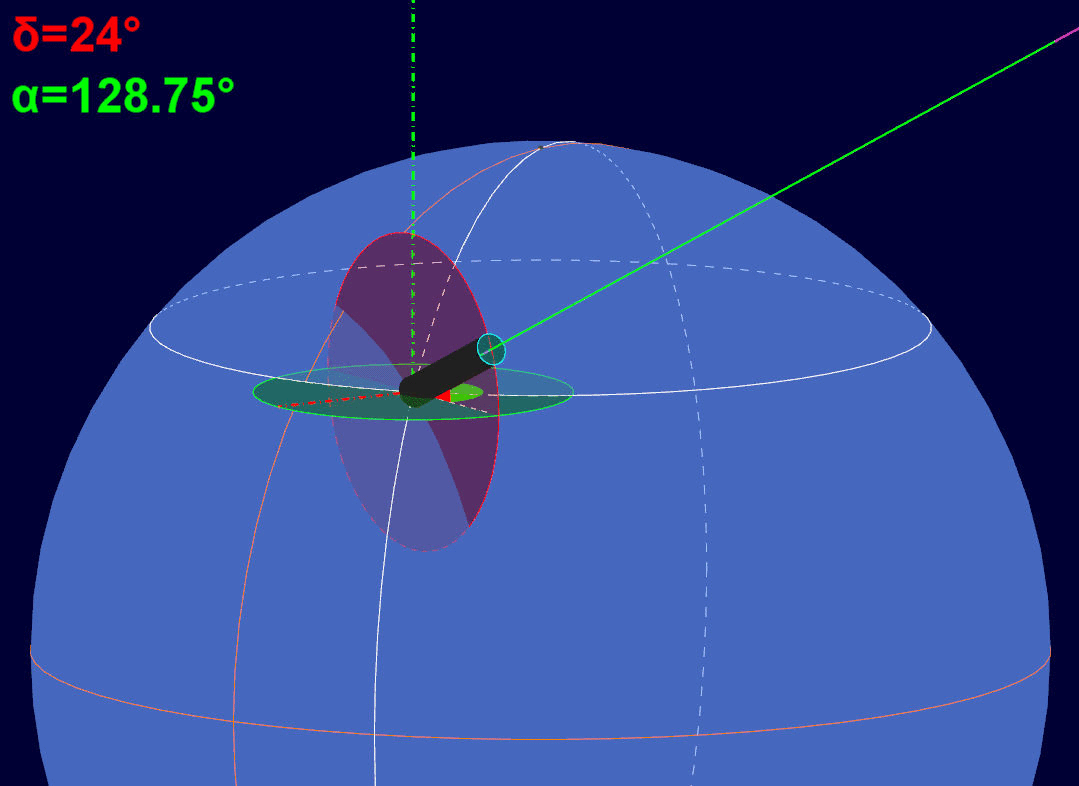
Il puntamento iniziale avviene facendo ruotare il telescopio attorno ai due assi della montatura, quello polare (ascensione retta) e quello della declinazione. Nella suddetta animazione si osserva l'asse ottico del telescopio, di colore verde, muoversi fino a sovrapporsi alla linea di mira color fucsia dell'astro oggetto di osservazione. All'istante in cui il telescopio inizia a muoversi, viene raffigurato anche il cerchio minore di colore rosso , che rappresenta il cerchio graduato della declinazione, presente sulla montatura, e l'asse di declinazione a tratto e punto di colore rosso. I due assi, quello polare e quello di declinazione, si mantengono sempre tra loro perpendicolari.

A questo punto, con il telescopio puntato verso l'astro, si dia inizio al movimento di rotazione terrestre. Si osservi la seguente animazione. Essa raffigura la rotazione della Terra fino a quando l'oggetto osservato non passa per il meridiano del luogo di osservazione.

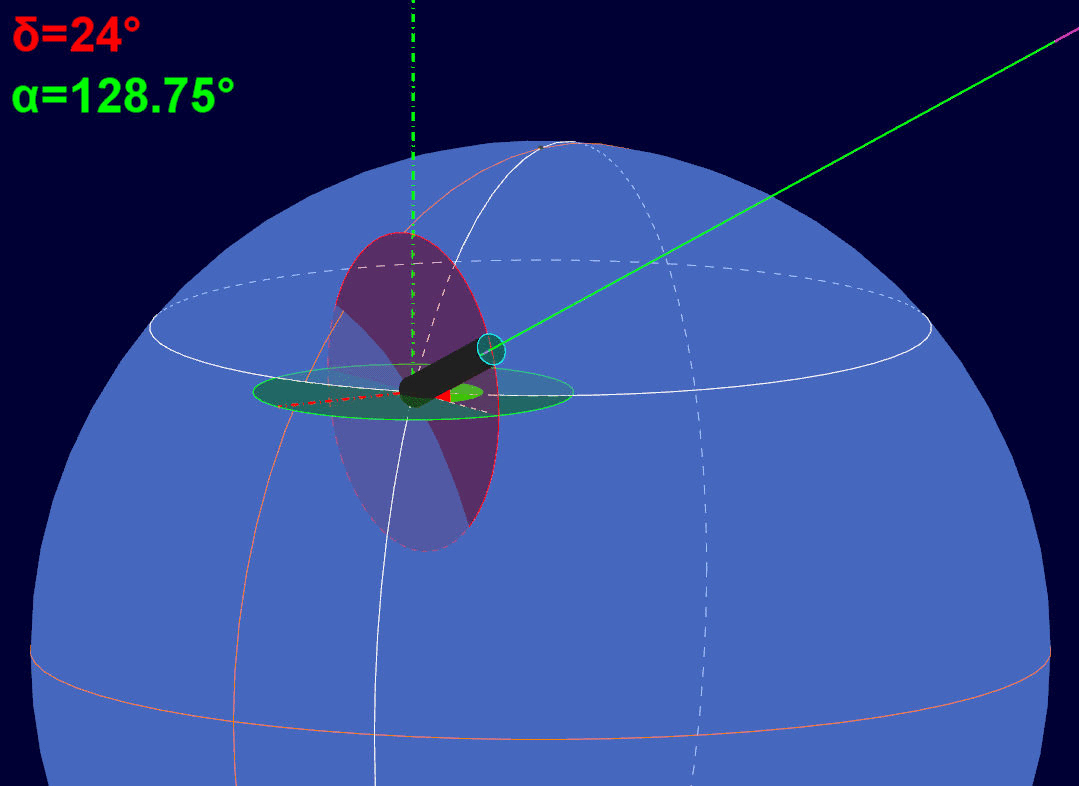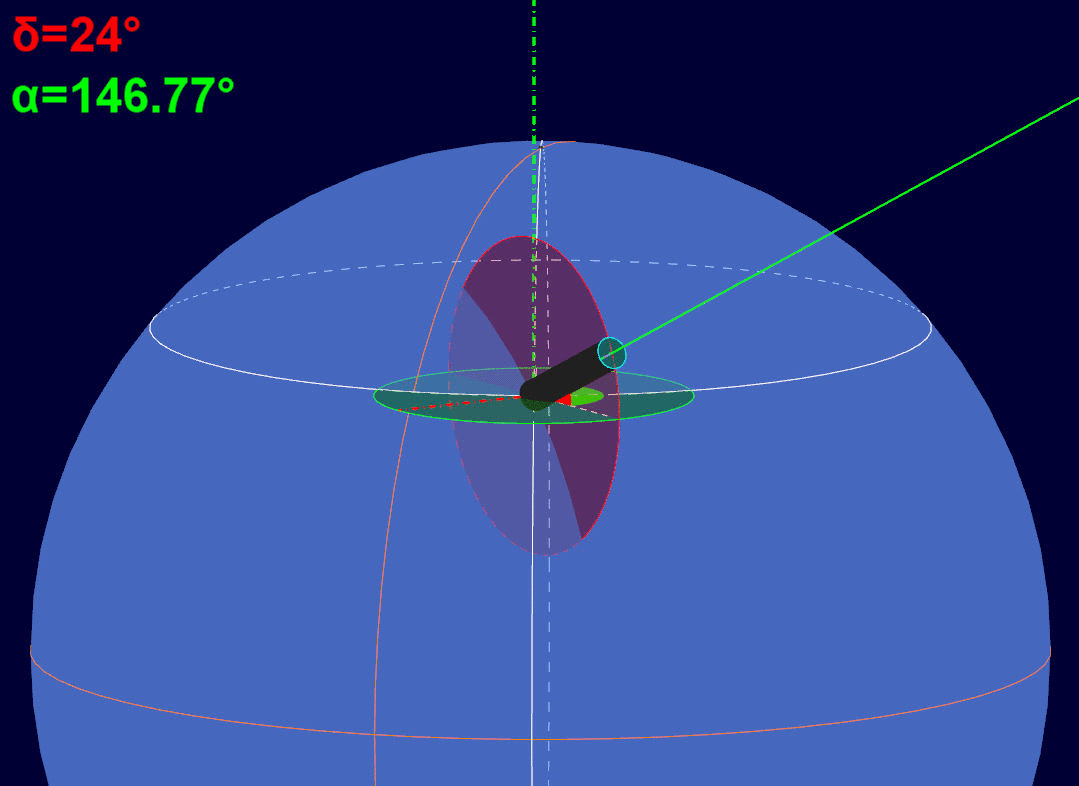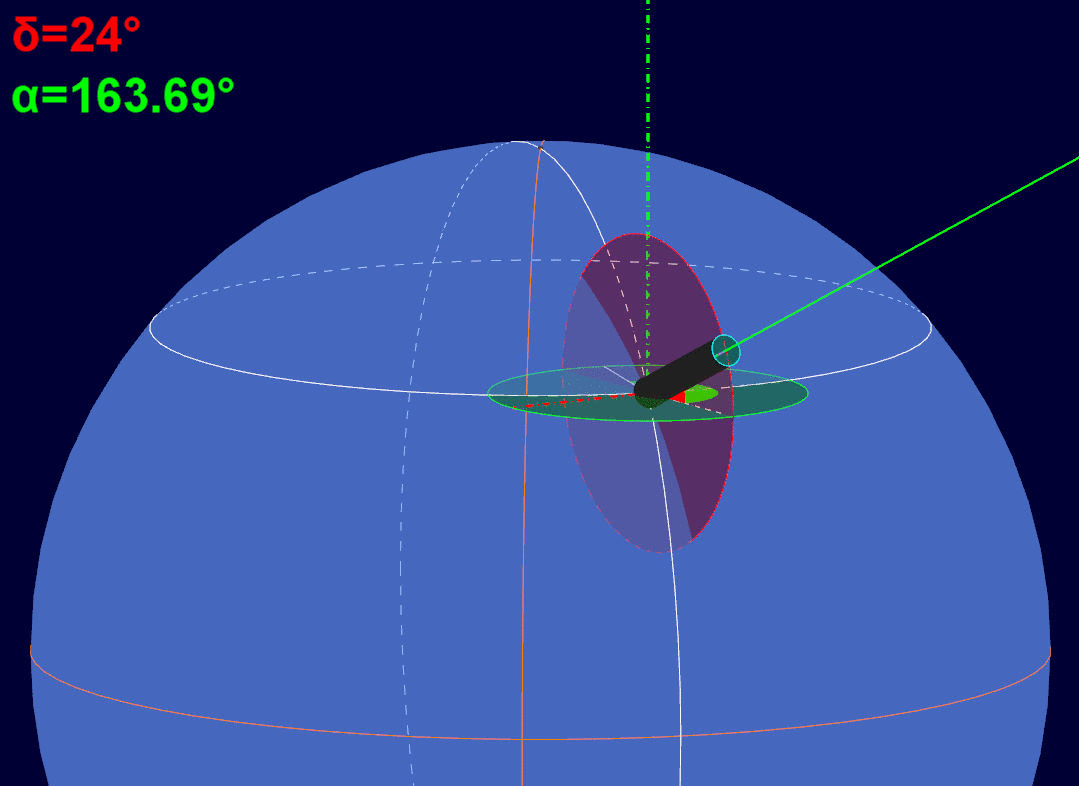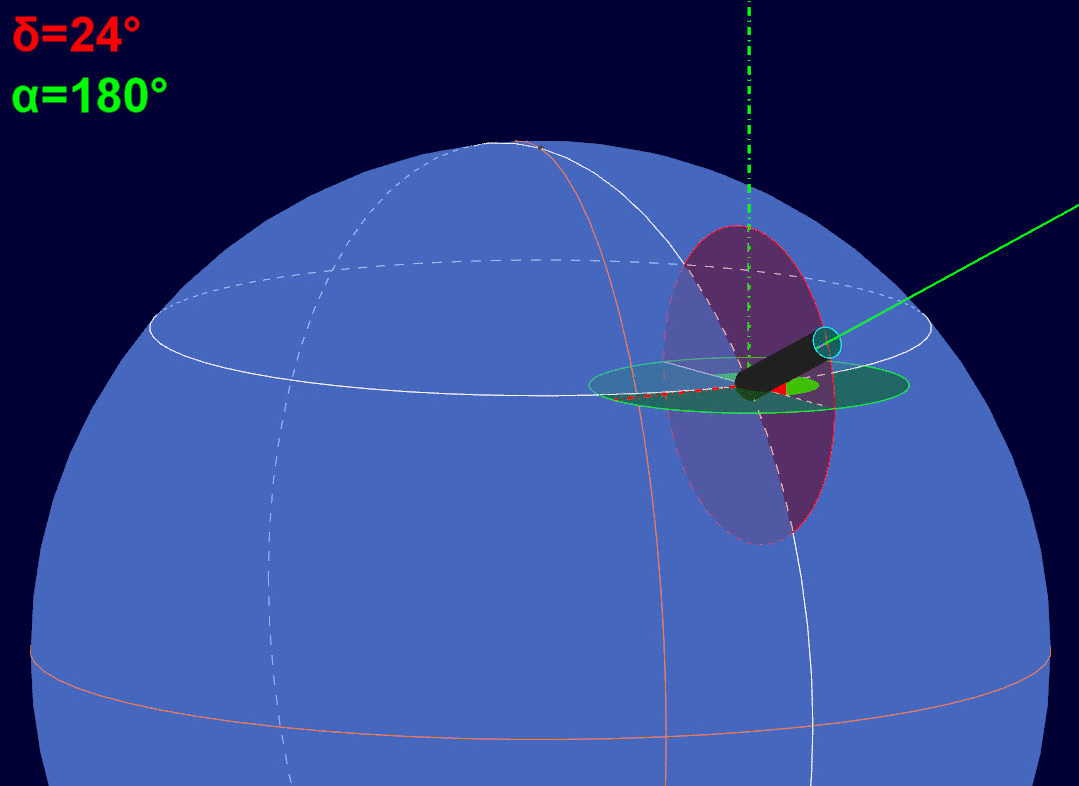
Si noti come l'angolo di declinazione (rosso) resti costante, mentre viene aggiornato solo quello di ascensione retta (verde). In pratica, la montatura equatoriale, per tenere puntato l'oggetto osservato, varia solo l'angolo di ascensione retta, compensando in tal modo il movimento di rotazione terrestre.

Perché ciò è possibile ?

Si osservi dal polo nord celeste il modello geometrico con il telescopio già puntato verso l'astro da osservare, come nella seguente figura:

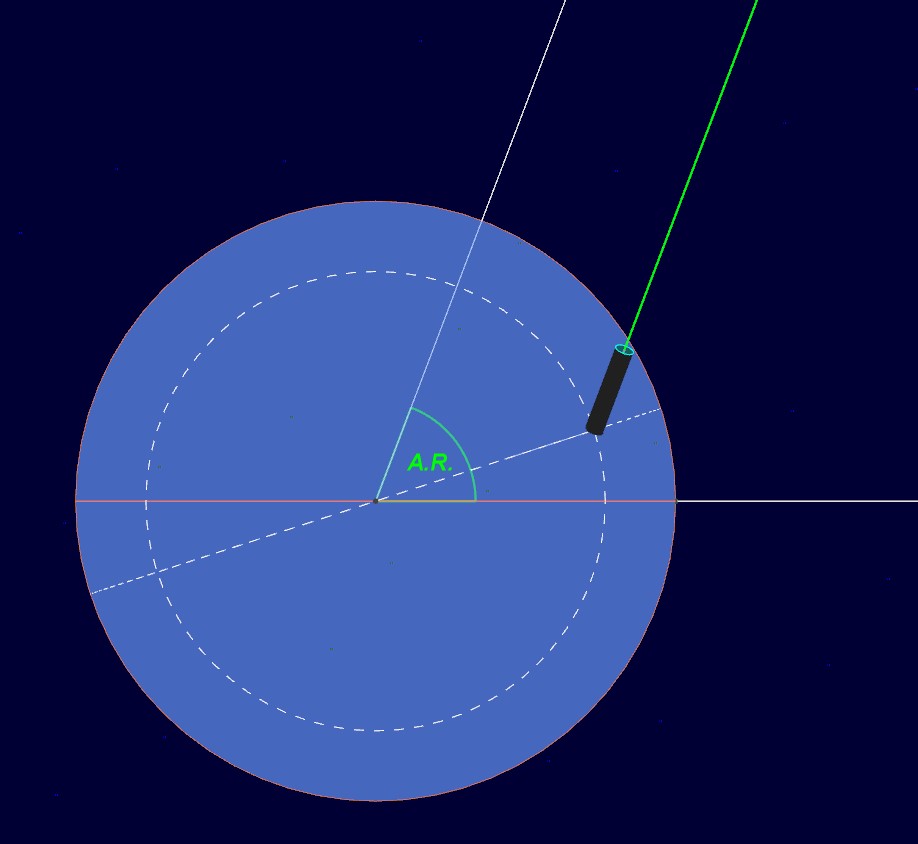
Quello indicato con "A.R." è l'angolo di ascensione retta dell'astro. Si ponga attenzione sulle semirette bianca e verde.  La prima parte dal centro della Terra e passa per la proiezione ortogonale dell'astro sul piano equatoriale celeste. La seconda è quella già vista prima, ossia l'asse ottico del telescopio collimato con la linea di mira dell'astro.  A causa dell'enorme distanza dell'astro dalla Terra (nel caso del Sole sono già 150 milioni di chilometri), le due suddette semirette risultano tra loro praticamente parallele. E questo parallelismo si conserva anche durante la rotazione della Terra attorno al proprio asse, come si nota in questa animazione:

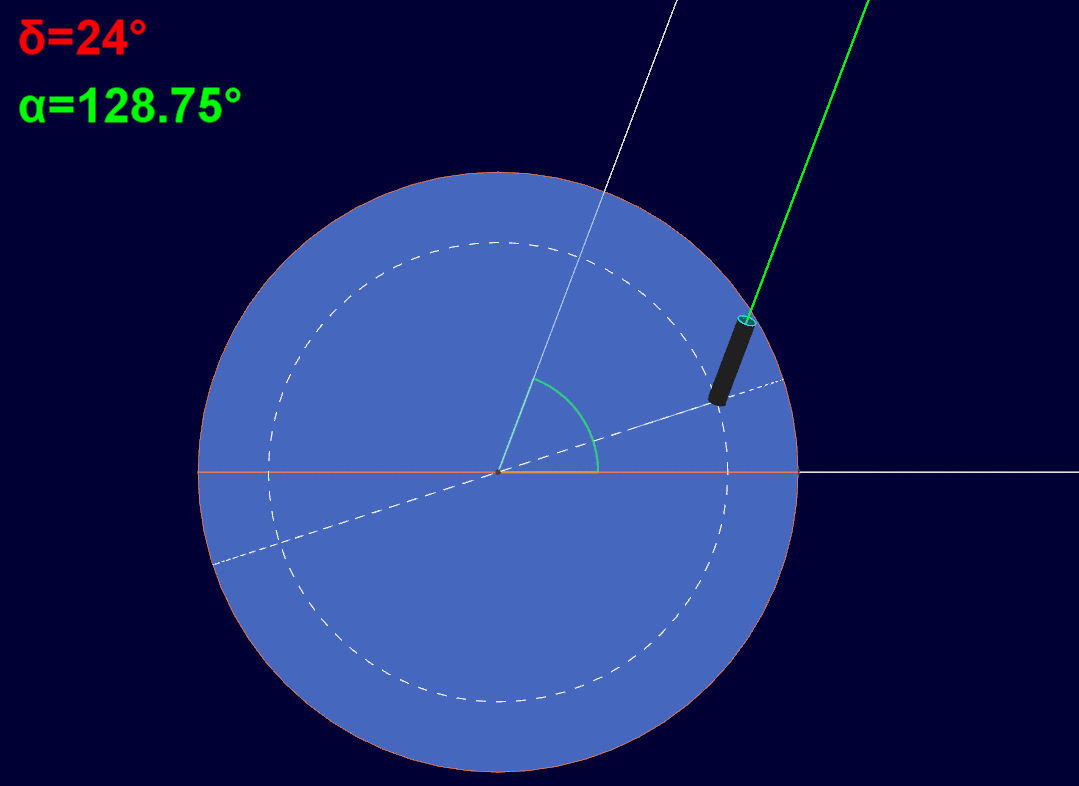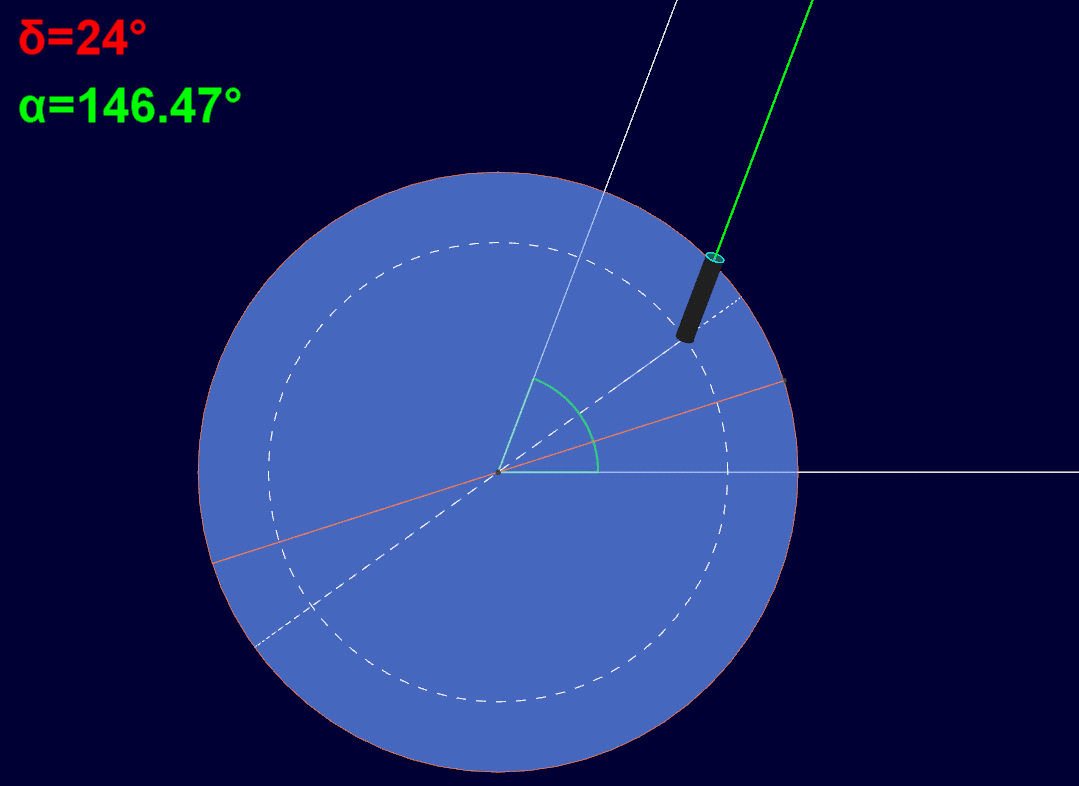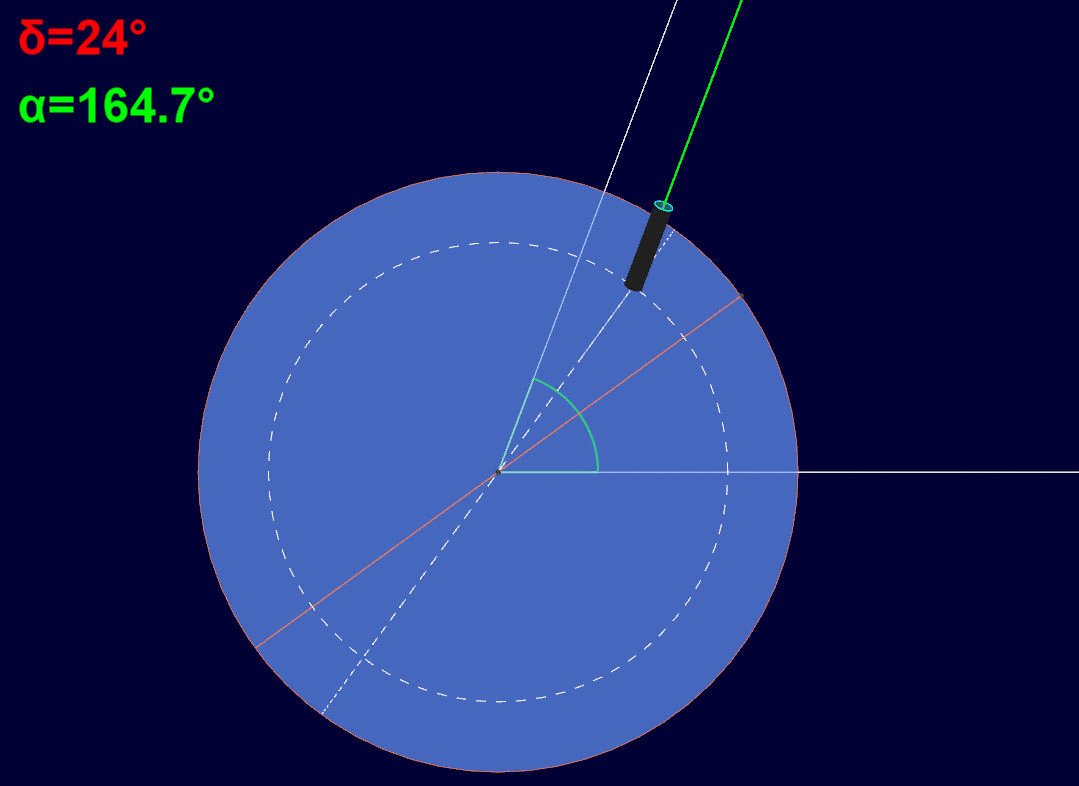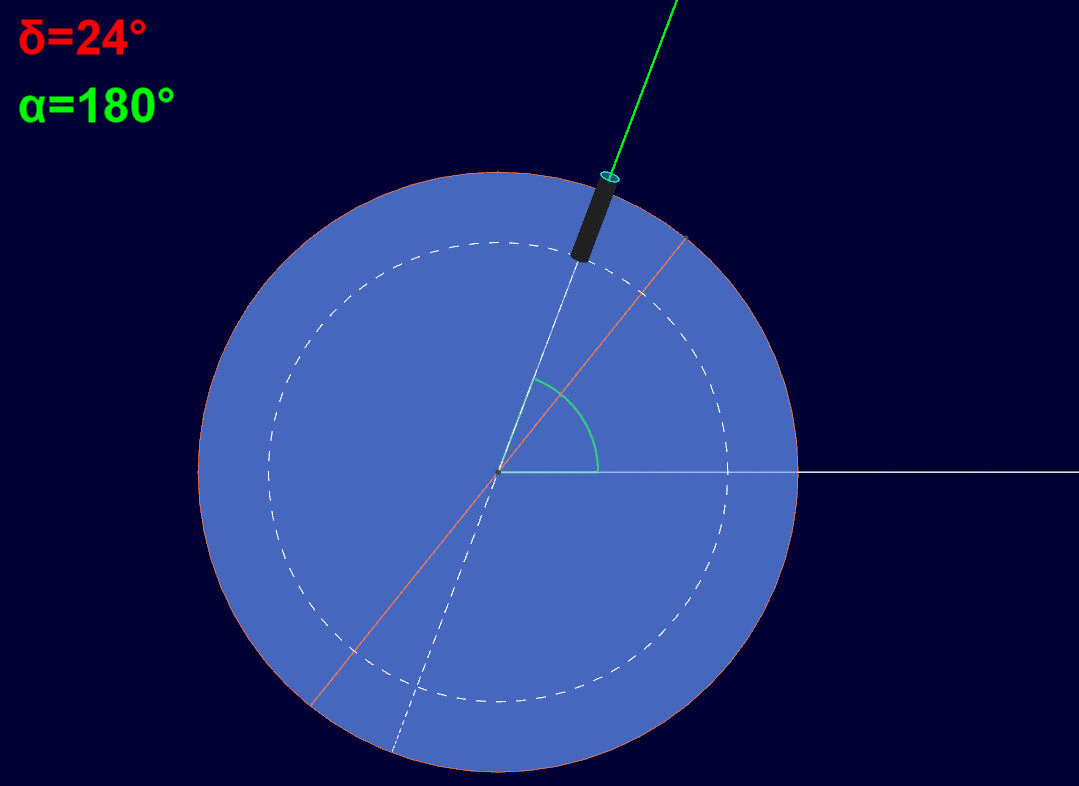
Quanto sopra fa si che alla rotazione della Terra di un certo angolo attorno al proprio asse, corrisponda, attraverso l movimentazione del telescopio attorno all'asse di ascensione retta, uno stesso angolo in verso opposto, così da compensare il moto apparente dell'astro nella sfera celeste.

Si osservi ora di fianco il modello geometrico, sempre con il telescopio già puntato verso l'astro da osservare, come nella seguente figura:

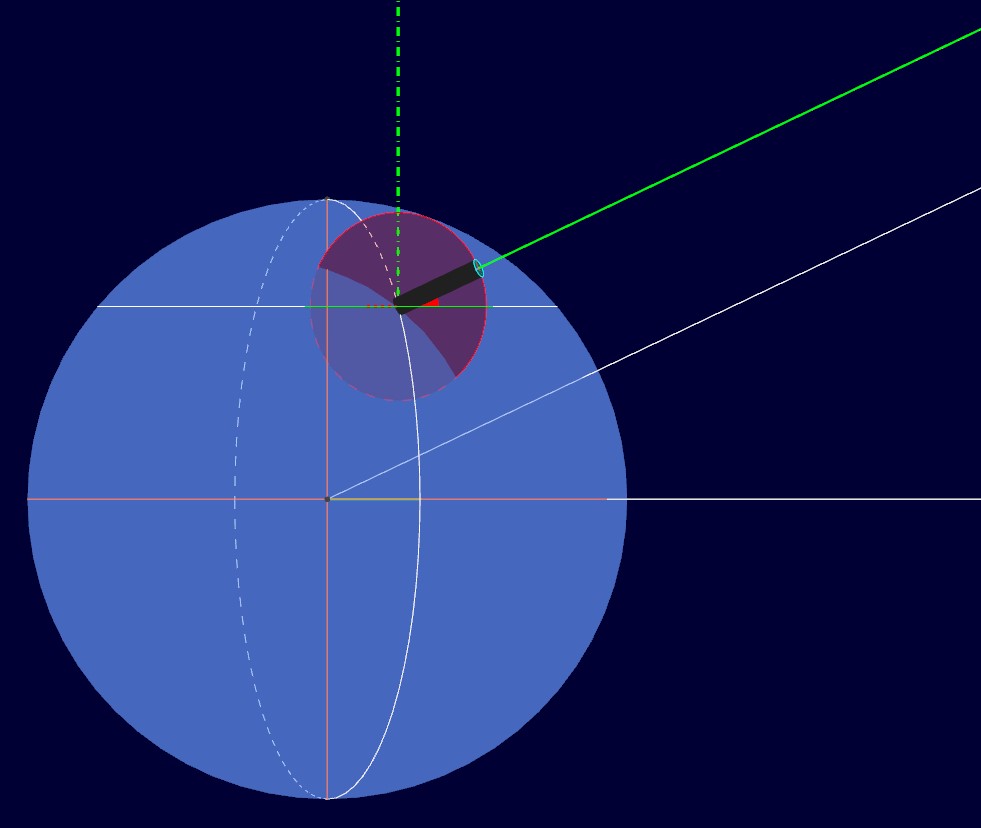
In questa immagine, la semiretta bianca congiunge il centro della Terra con l'astro oggetto di osservazione. Anche in questo caso, si nota che le due semirette, quella bianca e quella verde, sono tra loro praticamente parallele, e lo restano anche durante la rotazione della Terra.

E', dunque, l'elevatissima distanza degli astri dalla Terra a far si che , con le montature equatoriali, basti muovere il telescopio solo attorno all'asse di ascensione retta, restando, invece, praticamente inalterato l'angolo di declinazione. Questo rende le montature equatoriali motorizzate particolarmente adatte all'osservazione di oggetti del profondo cielo, con riprese che durano spesso molte ore.

Al seguente LINK troverete il modello geometrico da me realizzato con Geogebra, utilizzabile online.