Categorie: Relatività
Tags: coordinate cartesiane coordinate polari metrica tensore metrico vettori base
Scritto da: Fabrizio
Commenti:7
Mettiamoci alla prova con la Relatività Generale - verso la metrica
Questo articolo fa parte della sezione "METTIAMOCI ALLA PROVA!" all'interno della Relatività Generale al microscopio
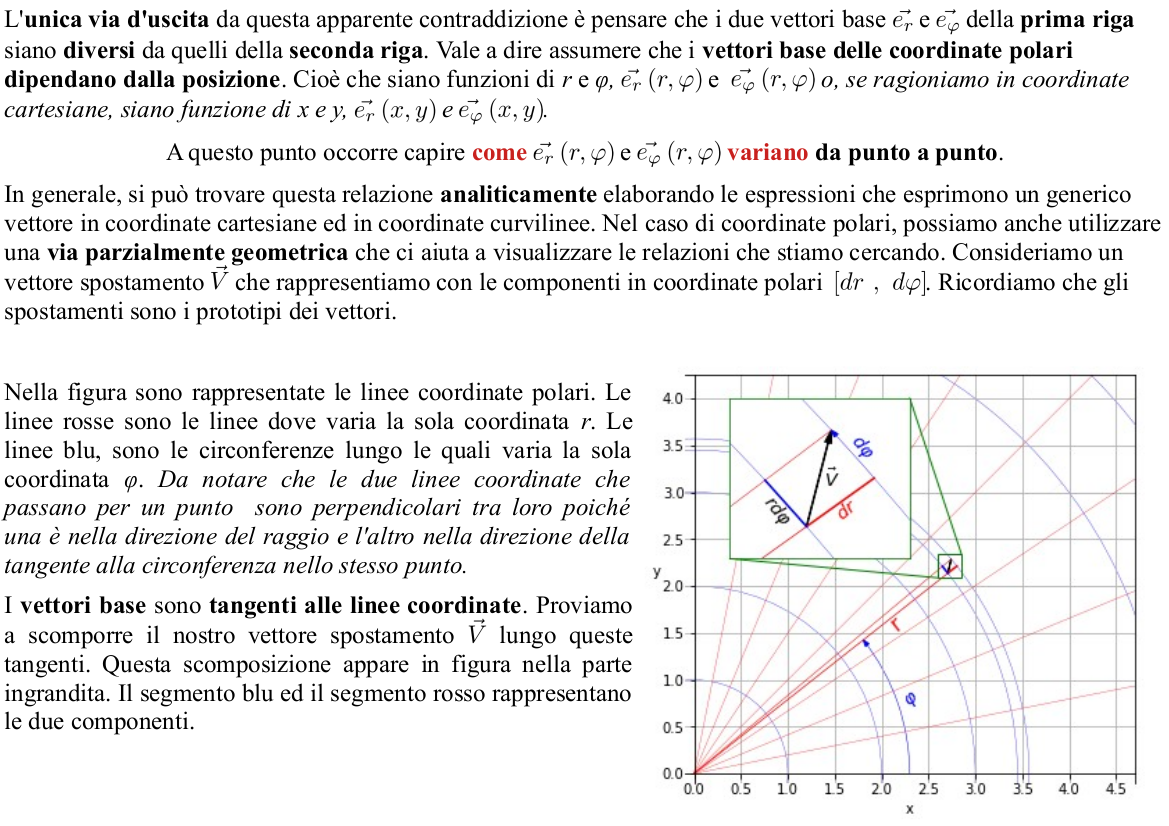
In questo articolo propongo alcuni degli argomenti affrontati da Enzo nel 6° articolo della serie “La relatività Generale al microscopio” applicati al caso particolare delle coordinate cartesiane e coordinate polari nello spazio Euclideo. L'obiettivo è di illustrare tramite queste due coordinate il percorso che porta al tensore metrico o metrica.
Mi permetto anche alcune digressioni che spero possano fornire qualche spunto che aiuti la comprensione dell'argomento. Inizio subito con una di queste.
Credo che possa aiutare quello che disse Einstein sul percorso che lo portò alla formulazione della relatività generale. Il senso di quello che disse è approssimativamente questo:
... Nel 1908 ebbi l'idea che le cose in caduta libera (per una piccola estensione di spazio) si comportano nello stesso modo in un campo gravitazionale e in uno spazio privo di gravitazione. ...Perché ci sono voluti altri sette anni per arrivare a formulare la teoria della Relatività Generale? La ragione principale è che non è facile liberarsi dall'idea che le coordinate debbano avere un immediato significato metrico.
Vale a dire che non possiamo ricavare la distanza tra due punti, siano essi nello spazio geometrico tridimensionale o in uno spazio quadrimensionale, direttamente delle loro coordinate.
Normalmente viene messo in evidenza il principio di equivalenza contenuto nella prima parte delle frase. Qui proviamo ad indagare sulla seconda parte della frase di Einstein.
La faccio utilizzando le usuali coordinate cartesiane e la loro relazione con le coordinate polari. Non è certo questo il caso che ha dato da pensare ad Einstein, ma per noi credo possa essere sufficiente.
Riprendo alcuni elementi visti nei precedenti articoli che ci serviranno a breve.
Un vettore può essere rappresentato dalle sue componenti in un sistema di coordinate. Per procedere dobbiamo approfondire il significato di queste componenti e come da queste si costruisce il vettore che rappresentano.
Il significato delle componenti in coordinate cartesiane è descritto in questo articolo di Enzo ed in forma più generica nell'appendice di questo articolo. Per il momento, qui mi limito ad uno spazio bidimensionale.
A ciascuna coordinata è associato un vettore base. Un qualsiasi vettore può essere rappresentato come somma pesata da opportuni coefficienti di questi vettori base. Le componenti indicano proprio i coefficienti che moltiplicano i vettori base.
7 commenti
Non posso trattenermi... il lavoro svolto da Fabry è veramente encomiabile, preciso e fondamentale per seguire il mio approccio giocoforza molto concentrato e, spesso, un po' vago...
Alla fine, penso, che l'unione dei nostri sforzi darà luogo a un manuale da tenere sempre sotto il ... cuscino.
Anche se non si fa normalmente, fatemi RINGRAZIARE apertamente il nostro bravissimo Fabrizio!!!
Gran bel lavoro, Fabrizio. Grazie.
I vettori base sono quelli altrimenti chiamati "versori" ?
Enzo, grazie per le considerazioni sul mio articolo. Quasi arrossisco.
Arturo, grazie per il tuo apprezzamento.
Credo che nella definizione di versore ci sia la proprietà di essere unitario. Qualcosa definibile come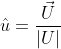
.
I vettori base delle coordinate cartesiane possiamo considerarli dei versori, cosi come quando si utilizzano vettori base unitari. Ma in generale i vettori base utilizzati in RG non sono versori.
Io leggo questi vostri meravigliosi articoli seduto in divano, senza carta né penna a portata di mano. In pieno relax. Li trovo enormemente consolatori perché intuisco che i calcoli sono complessi, ma non difficili e che se mi applicassi con un vero studio riuscirei a svolgerli.
Alberto grazie per il tuo commento.
Per me è molto incoraggiante sapere che questi articoli possono essere seguiti senza particolari difficoltà.
Se negli articoli ci fossero dei passaggi che vi risultassero più difficili, mi farebbe piacere che me li segnalaste.
Spero di poter trovare il modo di chiarire questi passaggi per farvi continuare la lettura.
Perché i vettori di base sono scritti con l'indice in basso? Finora un vettore "tradizionale" era sempre stato scritto con l'indice in alto (controvariante).
Giangiacomo, scusa per la mancata risposta alla tua domanda molto pertinente. Purtroppo la email che mi avvisa dei commenti è andata a finire nella cartella degli spam.
Rispondo ora molto in ritardo sperando che tu possa leggere ugualmente la risposta.
Vengono messi in basso per convenzione in modo da poter applicare la sommatoria di Einstein:
l'elemento va sommato per tutti i possibili valori dell'indice muto i .
Nota che l'indice di questi vettori base ha un diverso significato di quello che tu osservi viene messo in alto.
Nei vettori base indica l'i-esimo vettore base di una certa base, l'altro indica la i-esima componente di un vettore
in una certa base, come ad esempio nella espressione sopra è 
.