Riporto la soluzione della prima parte del quiz, ma lascio ancora in sospeso la seconda parte, quella più "giapponese". Il quiz, quindi, continua.

La soluzione per la prima parte è stata ricavata da Arturo  ed è leggermente diversa da quelle che avevo pensato io.

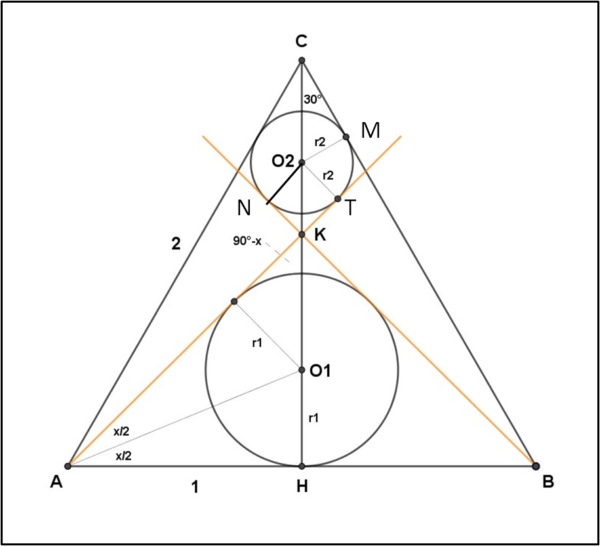
Ne presento una che sfrutta i triangoli BNO2 e BMO2, ovviamente uguali. Tuttavia, anch'essa porta a una relazione finale risolvibile solo con l'aiuto dei programmi reperibili su internet. Sfrutto la completa figura di Arturo per analizzare il problema.

Abbiamo che:

CH = KH + O2K + CO2

Ma sappiamo che:

KH = tan (x)

CO2 = 2r₂

O2T = O2K cos (x) = r₂

O2K = r2/cos(x)

CH = √3

Da cui:

√3 = tan(x) + 2r₂ + r₂/cos(x)

r₂(2 + 1/cos(x)) = √3 - tan(x)

r₂ = (√3 - sen(x)/cos(x))/(2 + 1/cos(x))

r₂ = (√3 cos(x) - sen(x))/(2cos(x) + 1)

che forse è più compatta di quella di Arturo, anche se continua a comportare la soluzione dell'equazione

r₁ = r₂

ossia:

tan(x/2) -  (√3 cos(x) - sen(x))/(2cos(x) + 1) = 0

Risolvendola con l'aiuto del web si ottiene:

x ∼ 35°. 27

in perfetto accordo con Arturo.

Da cui:

r₁ = r₂ ∼ 0.3178

Bene, molto bene... anche se rimango dell'idea che forse si potrebbe fare meglio...

Tuttavia, rimane un risultato approssimato! Ricordiamoci la differenza tra:

x  ∼ 1.4142

e

x = √2

I due risultati possono essere considerati identici, ma il secondo ha il SEGNO DI UGUALE e non di CIRCA UGUALE.

Ne segue che si può fare di meglio nel cercare il valore di r₁ = r₂ rendendolo veramente uguale a un certo numero. E lo si può fare senza dover calcolare prima l'angolo x.

Io ho trovato due metodi: il primo, sicuramente corretto, porta a un'equazione di terzo grado che è troppo "noiosa" da risolvere. Il secondo, invece, che si riferisce proprio alla tavoletta giapponese, è molto più rapido e porta anche lui a un risultato PERFETTO, senza alcun "circa" ...

Inizio col primo, anche se poi lo lasceremo incompiuto... ci servirà comunque per ricordare una formula di trigonometria poco usata, ma spesso molto utile.

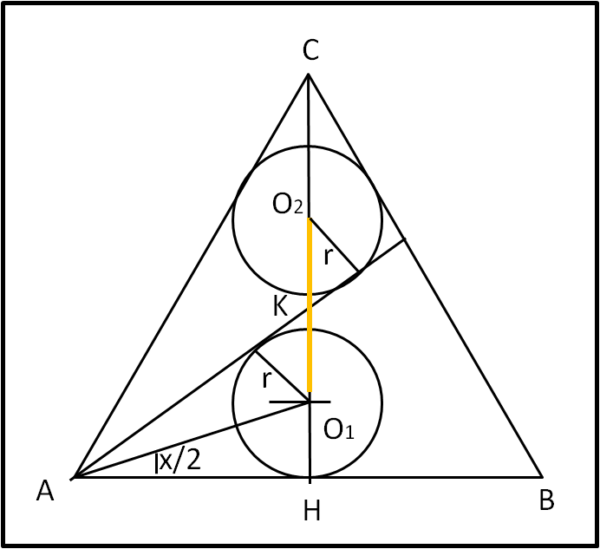
Giriamo un poco il problema e disegniamo la figura con r₁ = r₂

La faccenda si semplifica di molto e possiamo scrivere :

CH =  O1H + O2O1 + O2H

Ma

O2O1 = 2 O2K

dato che r₁ = r₂ = r

E otteniamo:

√3 = 2r + 2r/cos(x) + r = 3r + 2r/cos(x)

A questo punto facciamo entrare in ballo una relazione trigonometrica che prima o poi dimostreremo:

cos (x) = (1 - tan²(x/2))/(1 + tan²(x/2))

ma sappiamo che:

r = tan(x/2)

ne segue:

√3 = 3r + 2r/((1 - r²)/(1 + r²))

√3 = 3r + 2r(1 + r²)/(1 - r²)

(√3 - 3r)(1 - r²) = 2r(1 + r²)

√3 - √3r² - 3r + 3r³ = 2r + 2 r³

r³ - √3r² - 5r + √3 = 0

N.B.: la stessa equazione poteva velocemente essere calcolata anche ricordando che r = tan(x/2) e che:

CH = 2 tan(a/2)/cos(x) + 3 tan(x/2) = t2 an(x/2)( 1 + tan(x/2))/(1 - tan(x/2)  + 3 tan(x/2) = √3

Ponendo tan(x/2) = t, si ha subito:

2t(1 + t²)/(1 - t²) + 3t = √3

2t + 2t³ + 3t - 3t² = √3 - √3t²

e quindi:

t3 - √3t² - 5t + √3 = 0

che è la stessa equazione di prima, dato che r = t = tan(x/2)

L'equazione è sicuramente giusta, dato che soddisfa il risultato, ma è inutile proseguire su questa strada e conviene usare un altro metodo per ottenere r in modo indipendente dall'angolo x.

Vi lascio ancora un po' di tempo per risolvere questa parte del quiz...

 

QUI il quiz

QUI la seconda parte della soluzione e (forse) un nuovo teorema

QUI la dimostrazione del nuovo "Teorema di Zappalà"!