Il quiz dei due cerchi, "incatenati" al triangolo equilatero, sembra aver perso di interesse. Peccato... perché proprio la seconda parte  è quella più interessante, che ci permette addirittura di enunciare un "nuovo" teorema, simile ai tanti ricavati dagli antichi greci. A quanto mi risulta non mi sembra che sia mai stato enunciato, ma potrei sbagliarmi. Comunque un piccolissimo tassello geometrico in più del nostro circolo.

La seconda parte del problema, quella più "giapponese", sembrerebbe più difficile della prima, dato che l'angolo a delle rette che partono dai vertici sembra un requisito fondamentale per permettere di ricavare il raggio r. E, invece, non è così e per risolvere il piccolo enigma basta un'equazione di secondo grado.

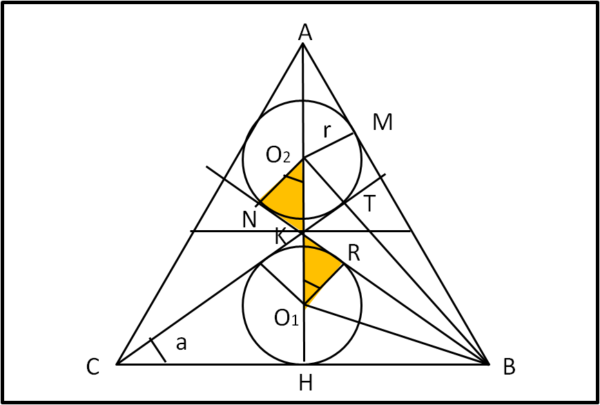
Consideriamo la figura che segue che illustra proprio il caso particolare in cui r₁ = r₂ = r.

Invece che su segmenti, lavoriamo su delle aree. In particolare vogliamo determinare l'area del triangolo rettangolo ABH, pari a metà di quella del triangolo equilatero di partenza: niente di più facile...

A_ABH = 1/2 AH · HB = 1/2 · 1 · √3 = √3/2

Tuttavia, vogliamo anche determinare questa stessa area utilizzando altri triangoli che compaiono nella figura e i cui segmenti fondamentali sono riportati di seguito:

AM = √(4r² – r²) = √3r

MB = BN = 2 - √3r

HB = RB = 1

Inoltre, è immediato concludere che i due triangoli (colorati in arancione) sono congruenti, ossia:

A_O2NK = A_KRO1

Scriviamo, perciò, la seguente relazione, facilmente verificabile:

A_ABH = A_AMO2 + A_O2MB + _ABO2N – A_O2NK + A_O1RB + A_O1HB + A_KRO1

A_ABH = A_AMO2 + 2A_O2MB + 2A_O1RB

Abbiamo, semplicemente, sommato e sottratto triangoli uguali. In particolare, sono sparite le uniche aree dipendenti dall'angolo a.

Passando ai valori numerici:

√3/2 = √3r²/2+ r(2 - √3r ) + r = √3r²/2+ 2r - √3r² + r

√3r²/2 – 3r + √3/2 = 0

√3r2 – 6r + √3 = 0

Una semplice equazione di secondo grado, in cui l'unica variabile è proprio il raggio r. Risolviamola con il metodo che vogliamo ed essa porta a due valori reali di r

r = √3 - √2

e

r' = √3 + √2

La seconda soluzione è, ovviamente da scartare, dato che il cerchio non sarebbe inscrivibile nel triangolo equilatero di partenza.

A questo punto termina la tavoletta giapponese...

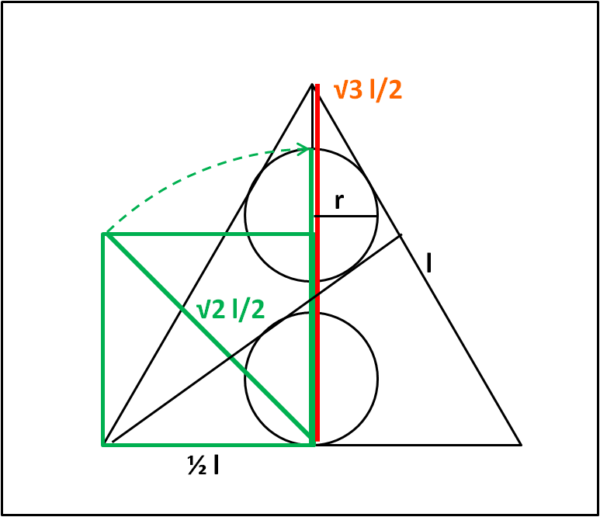
Il risultato che abbiamo trovato è ovviamente simile a quello trovato nella puntata precedente, ma, questa volta, è un risultato ESATTO. Non solo esatto, però, ma esprimibile in maniera geometrica e veramente semplice, come mostra la figura che segue

Nel caso in questione (triangolo con lato l uguale a 2), ci dice che il raggio del cerchio è esattamente uguale alla differenza tra altezza del triangolo e diagonale del quadrato di lato 1/2 l = 1. D'altra parte, la dimostrazione precedente, ci dice che la coincidenza non è una caso, ma la realtà geometrica dei fatti. Possiamo, perciò, enunciare il seguente teorema:

Ipotesi: In un triangolo equilatero, di lato l, vengano tracciate due linee uscenti da due vertici in modo da costruire due cerchi uguali, tangenti alle due rette e ai lati del triangolo.

Tesi: Il raggio dei due cerchi è pari alla differenza tra l'altezza del triangolo e la diagonale del quadrato di lato pari alla metà di quello del triangolo.

Ossia:

r = l/2(√3 - √2)

Ovviamente, la dimostrazione è quella che abbiamo appena dato!

Niente di speciale, ovviamente... ma è stato fatto un piccolo passo in più rispetto ai ... giapponesi.

La faccenda mi interessa particolarmente, dato che mi gira per la testa che la dimostrazione possa anche essere data in modo puramente geometrico e senza bisogno di un'equazione (inoltre, il valore r', che abbiamo scartato, riveste un certo interesse).

Per il momento mi fermo qui e sono, ovviamente, benvenute idee da parte vostra che possano ancora migliorare o generalizzare il "nuovo" (forse) teorema, magari con l'ausilio di qualche animazione. Nel nostro "piccolissimo" abbiamo scritto qualcosa che nemmeno Euclide aveva scritto, anche se con un enorme aiuto da parte della geometria giapponese. Tuttavia, possiamo accontentarci...

P.S.: non prendete sul serio la vignetta di copertina... sto solo scherzando!

 

 

 

 

 

 

Il quiz lo trovate QUI e la prima parte della soluzione QUI

QUI la seconda parte della soluzione e (forse) un nuovo teorema

QUI la dimostrazione del nuovo "Teorema di Zappalà"!