Questo articolo è stato inserito nella pagina d'archivio dedicata a Matematica e Geometria

 

Cari amici, la generalizzazione del problema iniziale mi ha portato a cercare una nuova strada per descrivere il "fenomeno" geometrico. Una strada che mi è sembrata molto interessante e, all'apparenza almeno, del tutto inesplorata. Il bello è che potrebbe essere resa benissimo da una animazione (vero Arturo?) o permettere di costruire un qualche aggeggio concreto (vero Frank?). Fatemelo dire: possiamo chiamarlo "l'ultimo (ma anche il primo!) teorema di Zappalà o, meglio, di Zappalat" e che Fermat non me ne voglia!

 

Invece di considerare una retta che passa per il vertice, iniziamo inserendo dei cerchi all'interno del triangolo equilatero di lato 2. Anzi, iniziamo con un solo cerchio e poi lo sdoppiamo nel suo fratello gemello. Iniziando dall'alto, inseriamo dei cerchi che siano tangenti ai due lati del triangolo, il cui centro, ovviamente, si sposti lungo l'altezza BH, come mostra la Fig. 1.

Per ogni cerchio che disegniamo, inseriamo, tangente alla base AC, un fratello gemello. Possiamo continuare in questo gioco, in cui compaiono sempre due cerchi uguali, fino a un limite invalicabile, dato che mai e poi mai vogliamo fare intersecare i due cerchi (devono mantenere la loro privacy!). Al limite, quindi, ci spingiamo fino a che il cerchio superiore e quello inferiore siano tangenti tra loro, come mostra la Fig. 2.

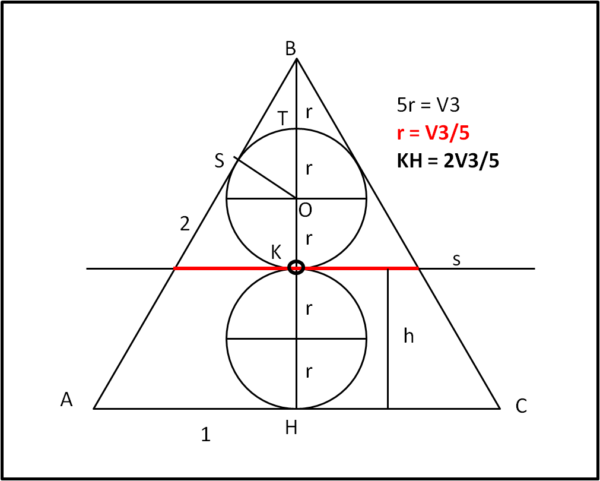
Bene. A questo punto è banale ricavare il raggio r dei due cerchi, un limite superiore e invalicabile. Quanti raggi sono contenuti nell'altezza del triangolo? Presto detto; i due cerchi sono uguali e, quindi, 4 raggi ci portano fino a punto T. Tuttavia sappiamo molto bene che, per costruzione, OB è l'ipotenusa del triangolo rettangolo BSO. Tuttavia, questo triangolo ha un angolo di 30° e l'altro di 60°, dato che è simile al triangolo ABH. Ne segue che l'ipotenusa deve essere il doppio del cateto minore che è proprio r. In conclusione:

BO= 2r

da cui si ottiene che:

BT = r

In poche parole, nell'altezza BH sono contenuti 5 raggi  e quindi:

r = BH/5

ossia

r = √3/5

dato che l'altezza BH è proprio uguale a √3.

Il punto K di tangenza tra di loro si trova a un distanza KH (che chiamiamo h) dalla base pari a:

KH = h = 2r = 2√3/5

Molto bene. Adesso, per rendere più "pratica" la nostra figura, immaginiamo di inserire una cerniera in K in modo che la retta s sia libera di ruotare attorno a K. In questo modo, sono sicuro che i tanti ingegneri del nostro Circolo avranno mille idee per rendere utilizzabile praticamente il "dispositivo" puramente geometrico. Mi raccomando, non mi deludete (il "praticone" Frank per primo, seguito da Arturo e da molti altri...).

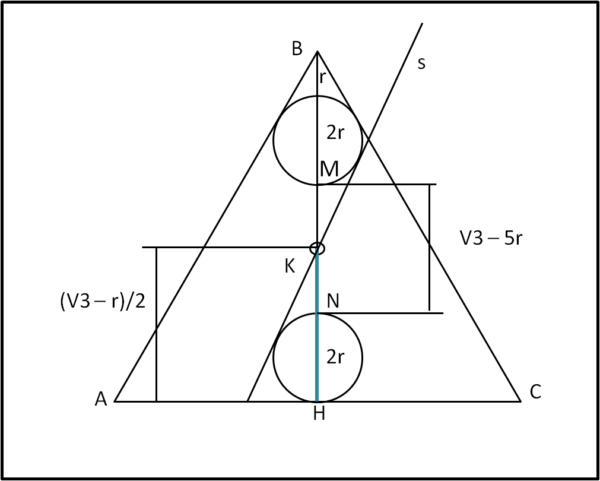
Facciamo perciò ruotare la nostra retta s attorno a K e vediamo cosa succede. In altre parole, basta considerare due cerchi minori del raggio limite precedente. Ne vediamo un caso qualsiasi in Fig. 3.

Il raggio r è ovviamente cambiato e nell'altezza BH sono adesso contenuti ben più di 5 raggi. La retta s continua a essere tangente ai due cerchi, comportando un fatto molto importante: la cerniera K deve stare a metà tra M e N, per ovvia simmetria della figura.  La retta s è ruotata attorno a K, ma anche K si è mossa portandosi verticalmente in un nuovo K.

Nessun problema... E' facilissimo determinare il valore di HK = h

MN = √3 - 5r

MK = KN = (√3 - 5r)/2

h = 2r + (√3 - 5r)/2 = (4r + √3 - 5r)/2

h = (√3 - r)/2

o, se preferiamo:

r = √3 - 2h

Verifichiamo questa relazione generale che vale per qualsiasi cerchio scelto. Lo facciamo per un cerchio talmente piccolo tale che il suo raggio vada a ZERO, come rappresentato in Fig. 4.

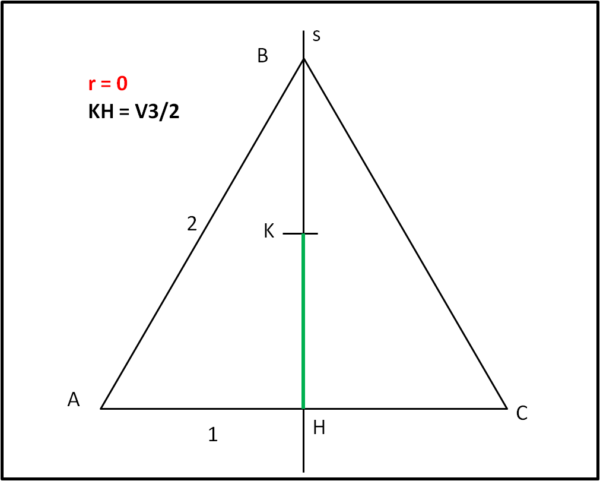
Beh... otterremo:

h = √3/2

Risultato più che atteso in quanto la cerniera deve spostarsi proprio a metà dell'altezza BH.

Ovviamente la formula deve valere anche per il caso iniziale, in cui avevamo il raggio massimo.

Il raggio valeva

r = √3/5

e, sostituendo:

h = (√3 - r)/2 = 4√3/10 = 2√3/5

come era ovvio aspettarsi.

Non ci resta che vedere l'intera faccenda come un un vero meccanismo (a cosa possa servire è compito, come detto, degli ingegneri e affini).

Iniziamo dalle condizioni in cui il raggio è uguale a zero, ossia in cui la retta s è verticale. Poi iniziamo a farla ruotare attorno a K in senso orario, mentre lo stesso K scende lungo la verticale, fino a raggiungere la posizione orizzontale, raggiungendo le condizioni di raggio massimo. Come si vede molto bene nella Fig. 5, "a scatti", la retta s interseca la base in punto P che si sposta verso sinistra fino a diventare il punto all'infinito quando raggiunge la posizione orizzontale.

Questo punto corrisponde a tutte le situazioni che possono essere di una qualche utilità. Ad esempio, quando la retta s è parallela al lato AB il punto P darà luogo a una distanza PK che è strettamente legata al triangolo equilatero e alla relazione che esiste tra raggio r e altezza h.

Insomma, tutte le configurazioni che si possono cercare e che lascio, ovviamente, alla vostra fantasia.

Particolare importanza ha, però, la configurazione in cui la retta s PASSA PER IL VERTICE A. Questa è proprio quella richiesta dalla tavoletta giapponese. Sappiamo già il risultato, ossia r = √3 - √2, da cui segue

h = √2/2.

Abbiamo, infatti:

h = (√3 - r)/2

da cui

h = (√3 - √3 +√2 )/2 = √2/2

Il caso particolare, in cui la retta s passa per A, comporta che l'altezza h della cerniera sia proprio uguale alla metà della diagonale del quadrato di lato la metà del lato del triangolo equilatero. In poche parole, il triangolo KHD, di Fig 6, è isoscele.

N.B: Attenzione a non farsi ingannare! Il punto K non coincide con il K dei due cerchi massimi di Fig. 2, ma gli è straordinariamente vicino. Ne so qualcosa...

Un'ulteriore riprova, riguardo al famoso angolo a, che non abbiamo assolutamente usato? Banale!

tan(a) = √2/2 = 0.7071...

da cui

a = 35.°26...

Vi invito caldamente a costruire il meccanismo, sperando che sia anche utile e, magari, dimostrare solo geometricamente che h vale proprio la metà della diagonale...

Parlando in termini realistici e concreti:

Dobbiamo costruire una macchina in cui vi è un asse rigido che gira di 90° attorno a un punto K , che a sua volta trasla verticalmente di una certa quantità calcolabile a priori. Questa traslazione è legata a una ben determinata legge (r in funzione di h). Senza nemmeno scomodare più i cerchi, bisogna solo determinare la posizione di K quando l'asta rigida passa per il punto A.

Buon divertimento e ... attendo anche l'animazione.  Qualsiasi Tizio e/o Sempronio che darà un contributo in tal senso  farà diventare il nuovo teorema il teorema di Zappalat-Tizio-Sempronio-.... Chi, invece, scoprirà che ho scoperto l'acqua calda... è meglio che taccia per sempre!!!

P.S.: mi piace ricordare ciò che ha detto Papalscherzone, alias Scherzy, intelligenza aliena ben conosciuta e apprezzata in tutta la nostra galassia (e forse anche in Andromeda, che ormai è "pappa e ciccia" con la nostra): "Un piccolo passo per la geometria, un passo enorme per un professore che riesce a passare da Euclide alla zuppa di pesce e poi ai tensori metrici con una leggerezza da fare invidia a Carla Fracci!". Sono, ovviamente lusingato, anche se la leggerezza di Carla Fracci è ben lontana dalla mia "stazza"... Che dirvi? No, non penso proprio che mi diano il Nobel per la matematica (non lo ha ottenuto postumo nemmeno Fermat), ma mi sono sicuramente divertito e spero anche voi !

Viva l'ironia, soprattutto se è diretta verso noi stessi!

P.P.S. (di Scherzy): ...ma soprattutto se è diretta verso il mio astrofisico in pensione preferito! (Sperando che non si arrabbi troppo per aver modificato il nome del teorema e inserito qualche immagine mentre lui dormiva come un angioletto...)