Prendiamo spunto dall'intrigante problema della capretta legata a una corda per ricordare un paradosso di Zenone, Blade Runner, una rana in miniatura e un'equazione trascendente.

 

Premessa... approssimativa

Partiamo da una considerazione che è il vero "succo" del problema:

Dire che

x = 1.4142...

è un risultato approssimato.

Dire che

x = √2

è un risultato esatto e poco importa se devo scriverlo numericamente in modo approssimato.

Sembrerebbe, a qualcuno, un controsenso, ma pensiamoci bene... Se ho una certa equazione che non riesco a risolvere, posso usare vari metodi per trovare il risultato. Ad esempio, posso utilizzare il metodo iterativo: si parte da un valore molto approssimato, si inserisce nell’equazione e se ne trova uno un po’ migliore; lo si inserisce di nuovo e via dicendo fino a ottenere una precisione sufficiente. Un classico esempio che abbiamo trattato a questo riguardo è quello relativo all'Equazione di Keplero (QUI, formula 20) che ci permette di calcolare con la voluta approssimazione l'anomalia eccentrica. Ben altra cosa è, invece, risolvere un'equazione e trovare che il risultato è proprio √2.

Avviciniamoci un po' alla volta al nostro problema. Per toccare con mano un risultato approssimato il modo migliore è riferirsi ai celebri paradossi di Zenone. Descriviamone uno a cui non abbiamo mai accennato, anche se è oltremodo arguto, pur assomigliando al ben più famoso paradosso di Achille e la tartaruga.

 

Il paradosso della dicotomia 

Immaginiamo che Atalanta debba percorrere una certa distanza ad una velocità costante. Per arrivare alla fine del percorso, Atalanta deve sicuramente percorrere metà dell'intero tratto. Ma per percorrere questa prima metà deve prima percorrere la sua metà e via dicendo... In parole matematiche siamo di fronte a una sequenza del tipo:

... 1/16, 1/8, 1/4, 1/2, 1

Questa descrizione richiede di completare un numero infinito di  tratti, cosa che Zenone considerava come impossibile. In realtà, infatti, ogni tratto è finito e quindi necessità di un certo tempo per essere percorso. Ma se il numero di tratti è infinito, allora ci vuole anche un  tempo infinito per completare il percorso. In altre parole, il percorso non può mai essere completato. Ma, dato che il ragionamento può essere applicato a una qualsiasi distanza, ne segue che nessuna distanza può mai essere completata, ossia il moto è IMPOSSIBILE. Notiamo che il paradosso può anche essere espresso invertendo i tratti. Dapprima Atalanta arriva a metà percorso, poi percorre la metà, poi la metà della metà e via dicendo... In tal modo si ha proprio la somma del tipo

1/2 + 1/4 + 1/8 + 1/16 + ...

Zenone era convinto che la somma di numeri positivi dovesse SEMPRE andare a infinito e quindi il ragionamento funzionava perfettamente. Oggi sappiamo che non è così, ma allora era argomento di gran disputa.

La sequenza originale, però, presenta un  ulteriore problema, dato che non esiste praticamente una prima distanza percorsa. Per tale ragione, non esiste nemmeno un vero inizio del movimento. La conclusione si rafforza ancora di più: qualsiasi movimento da un punto a un altro non solo non può essere completato, ma non può essere nemmeno iniziato, da cui il risultato che il movimento non è altro che un'illusione.

Non ridiamoci  troppo sopra, dato che la caduta di una mela è anch'essa solo una specie di illusione, dato che lei sta ferma ed è lo spaziotempo curvo che le va incontro...

 

Da Blade Runner a una rana

Questo paradosso ha stimolato il grande scrittore di fantascienza (e non solo) Philip K. Dyck a cambiare Atalanta con una rana e a scrivere un bellissimo racconto.  Ricordiamo tra le tante opere di Dick, le "Cronache del Dopobomba" e, soprattutto, il "Cacciatore di Androidi", su cui è basato il film capolavoro di Ridley Scott, Blade Runner.

Il racconto "La rana infaticabile" fa parte della raccolta "Le Presenza Invisibili".

L'adattamento del paradosso a un caso realmente fantascientifico avviene a seguito di una disputa tra due scienziati uno a favore della tesi di Zenone e l'altro contro. Decidono di fare una prova pratica e, allo scopo, utilizzano un lungo tubo al cui interno la rana può eseguire i suoi salti, sempre uguali, ma dove le dimensioni dell'animale continuano a dimezzarsi (e quindi anche la lunghezza del salto successivo). Insieme alla rana entra nel tubo anche uno dei due scienziati per verificare direttamente. L'esperimento non riesce a concludersi, dato che dopo vari dimezzamenti, i corpi della rana e dello scienziato diventano più piccoli delle molecole ed escono dal tubo prima di completare il percorso. Nessun vinto e nessun vincitore!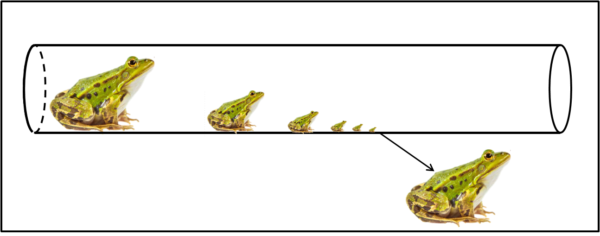

Lasciamo da parte il ranocchio e l'infinito finito (o il finito infinito) di Zenone e passiamo a un altro simpatico animale: una capretta. Abbiamo già fatto mangiare una capretta in un vecchio quiz, ma adesso semplifichiamo di molto le condizioni di partenza, complicando enormemente la possibilità di una soluzione esatta.

 

L'antico e irrisolto problema della capretta

Il problema è facilmente descrivibile. Consideriamo un campo circolare di tenera erbetta e piantiamo un  palo in un punto della sua circonferenza. Al palo leghiamo una capretta  che inizia a mangiare con frenesia fin dove glielo permette la corda che la tiene bloccata al palo. La domanda è "teoricamente" molto semplice: Quanto deve essere lunga la corda affinché la capretta riesca a mangiare metà dell'erbetta del campo?". Sembrerebbe un problema abbastanza banale, trattandosi in fondo di traiettorie circolari che si intersecano, come mostra la Fig. 1.

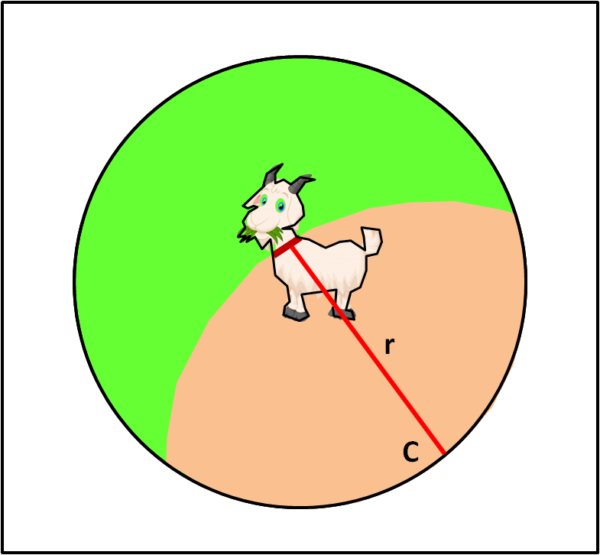
E, invece, il problema, proposto addirittura nel 1748, ha avuto una soluzione NON approssimata solo da pochissimo tempo, per merito del  matematico tedesco Ingo Ullisch.

 

Una lente geometrica

Per lente geometrica intendiamo l'intersezione tra due cerchi e la raffiguriamo, colorata in verde, nella Fig. 2

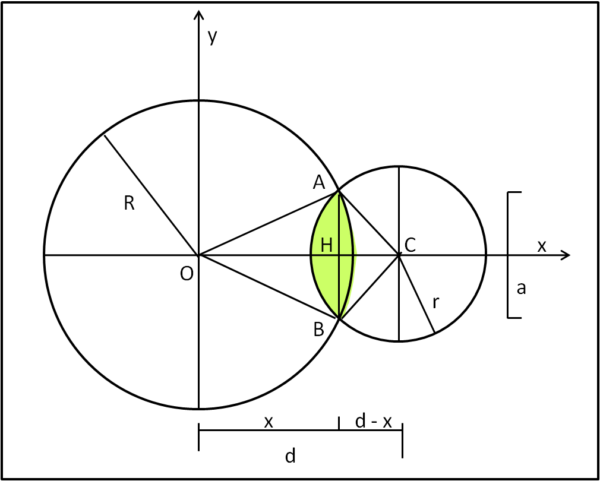
La figura definisce tutti i parametri utili per risolvere la nostra lente, ossia la la sua area. attraverso la distanza OH e  l'altezza AB. Essa è data dalla somma delle aree dei due segmenti circolari verdi, uno relativo al cerchio di raggio R e uno a quello di raggio r, entrambi con la stessa corda AB.

A questo punto, però, evitiamo un lavoro abbastanza lungo e monotono (chi vuole può sempre farlo, stando molto attento a non perdere dei "pezzi" per strada), dato che a noi interessa riferirci a una caso particolare, ossia a quello della capra legata a un palo situato su un punto della circonferenza di raggio R.

Una lente ... caprina

I calcoli sono piuttosto laboriosi (e un po' monotoni). E' decisamente più utile metterci fin da subito nelle condizioni particolari descritte dal problema della capra, in cui il centro C si trova esattamente sulla circonferenza di centro O (Fig. 3).

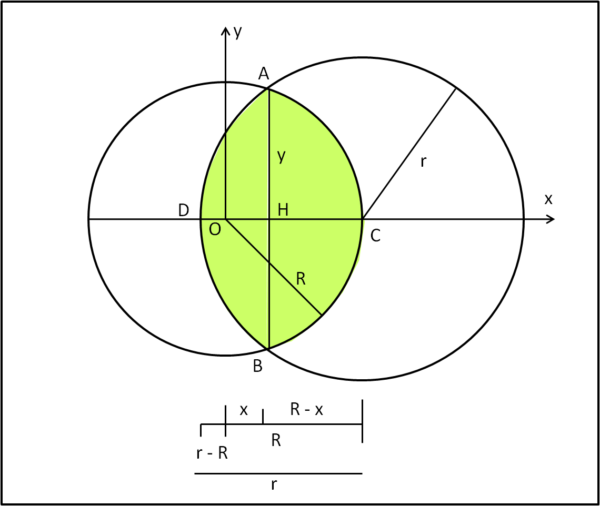
In tali condizioni R = d  e l'incognita rimane r. Porremo, in seguito, anche R = d = 1, senza limitare la generalità del risultato.

Procediamo con calma e scriviamo le equazioni delle due circonferenze nel sistema di coordinate rappresentato nella figura.

x² + y² = R²                     (circonferenza di centro O)

(R - x)² + y² = r²             (circonferenza di centro C)

Ricaviamo y² da entrambe e uguagliamo:

(R - x)² + (R² - x²) - r² = 0

R² + x² - 2Rx + R² - x² - r² = 0

2Rx = R² - r² + R²

x = (2R² - r² )/2R

con R = 1, si ha:

x = (2 - r²)/2                  .... (1)

Ricavato il valore x dei due punti intersezione (ossia OH), troviamo facilmente il valore di a = 2y

y² = R² - x² = R² - (d² - r² + R²)²/4d² = (4R²d² - (d² - r² + R²)²)/4d²

y = √(4R²d² - (d² - r² + R²)²)/2d

che, ponendo R = d = 1, diventa:

y =√(4 - (2 - r²)²)/2 =√(4r² - r⁴)/2

y = r√(4 - r²)/2                    .... (2)

A questo punto siamo pronti per il calcolo dell'area dell'intersezione. Utilizziamo la Fig. 4

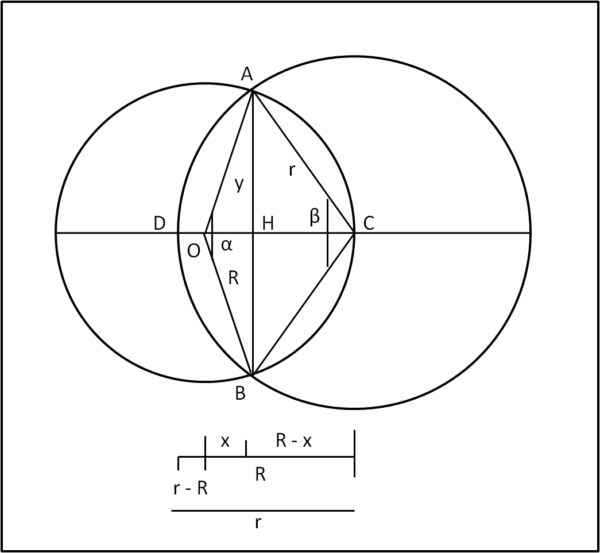
Essa è data dalla somma delle aree dei due segmenti circolari , uno relativo al cerchio di raggio R e uno a quello di raggio r. entrambi con la stessa corda AB =  2y

Chiamiamo A_R l'area del primo segmento e con A_r quella del secondo.

A_R = A_SR - A_TR

dove A_SR è l'area del settore circolare corrispondente all'arco AB del cerchio di raggio R e AT è l'area del triangolo OAB

A_SR = αR²/2

A_TR = 2y x/2

Dobbiamo ricavare l'angolo α e, per lo scopo, utilizziamo il triangolo OAH, da cui si ha subito:

R cos (α/2) = x = (2 - r²)/2  =  1 - r²/2

ponendo, come al solito, R = 1

cos (α/2) =  1 - r²/2

Ricordiamo che l'angolo (o l'arco) che ha per coseno un certo valore a viene indicato con arccos (a). Analogamente per il seno e la tangente.

α/2 = arccos (1 - r²/2)

Ne segue che

A_SR = αR²/2 = α/2

A_SR =  arccos (1 - r²/2)

Notiamo che abbiamo scritto l'area del settore in funzione della sola incognita r.

Passiamo al triangolo OAB

A_TR = 2yx/2 = yx                     .... (4)      (lasciamolo in questa forma)

A_R = arccos (1 - r²/2) - yx

Seguiamo un analogo procedimento per ottenere il secondo segmento circolare

A_r = A_Sr - A_Tr

A_Sr = ßr²/2

Non conosciamo l'angolo ß, ma lo possiamo scrivere in funzione di α e, quindi, di r (l'unica incognita, ricordiamoci!)

R cos(α/2) + r cos (ß/2) = R

r cos (ß/2) = R - R cos(α/2) =

per R = 1

cos(β/2) = (1 - cos (α/2))/r

cos(β/2) = 1/r - (1 - r²/2)/r = 1/r - 1/r + r²/2r

cos(β/2) = r/2

β/2 = arccos (r/2)

A_Sr = r²β/2

A_Sr = r² arccos (r/2)

Non ci resta che calcolare l'area del triangolo AHC, ossia A_Tr

A_Tr = 2y (R - x)/2 = y(1 - x)

A_Tr =  y - yx                 (lasciamo anch'esso in questa forma).

Ricordando che:

A_r = A_Sr - A_Tr

Ne segue:

Ar = r² arccos (r/2) - y + yx

Non ci resta che sommare i due segmenti circolari, ossia:

A = A_R + Ar

A = arccos (1 - r²/2) - yx  + r² arccos (r/2) - y + yx

A = arccos (1 - r²/2) + r² arccos (r/2) - y

Inseriamo, infine, il valore di y in funzione di r

A = arccos (1 - r²/2) + r² arccos (r/2) - r√(4 - r²)/2

Questa è l'area di prato mangiata dalla capretta. Ovviamente si risolverebbe tutto sapendo quanto vale r. Ma il punto chiave sta proprio qui, dato che noi non conosciamo la lunghezza della corda r, ma solo l'area A che vogliamo riesca a mangiare. Questa area vale la metà di quella del cerchio di raggio R, ossia:

A = πR²/2 = π/2

Per cui otteniamo l' equazione

arccos (1 - r²/2) + r² arccos (r/2) - r√(4 - r²)/2 - π/2 = 0

nella sola incognita r.

Facile a dirsi, ma non a farsi, dato che l'equazione è trascendente!

L'unico modo per risolverla è graficamente o per approssimazioni successive, ottenendo il risultato:

r = 1. 15872847 ...

In altre parole, un valore approssimato ma non esatto. Fino a poco tempo fa, però... dato che un matematico tedesco è riuscito a risolverla in modo esatto. Nel suo piccolo, e un po' come se avessimo trovato la soluzione esatta del problema dei tre corpi! Non confrontiamo, ovviamente, il moto di un corpo celeste con la corda che lega una capretta... ma è sempre un risultato cercato da più di due secoli e finalmente trovato. Non pretendete certo che io vi racconti il metodo seguito, che abbisogna del passaggio ai numeri complessi e tanta matematica superiore. Oltretutto, a quanto mi risulta, non è ancora stato pubblicato ufficialmente, ma ha ricevuto il "placet" da una commissione di matematici illustri.

Finalmente, sappiamo esattamente la lunghezza della corda: la capretta è libera di mangiare!

P.S.1: il problema è anche stato portato nelle tre dimensioni e si sta lavorando per la sua soluzione, insieme ad altre estensioni possibili, variando il punto in cui mettere il palo della capretta...

P.S.2: La capretta non è nuova nei nostri quiz...