Categorie: Matematica
Tags: cerchio ellisse ellissi geometria analitica Giappone quiz samurai Sangaku
Scritto da: Vincenzo Zappalà
Commenti:7
Una leggenda giapponese ***
Torniamo alla geometria analitica...
In realtà, questo quiz non ha un vero riscontro con la realtà, ma si riferisce a una leggenda "inventata" da me. Tuttavia, potrebbe essere ambientato benissimo nel periodo giapponese Edo, quando si ebbe una fioritura incredibile dell'algebra e della geometria nel Giappone dei Samurai. La soluzione è ampiamente alla portata di una preparazione a livello liceale o simile.
Un vecchio giapponese, molto ricco, lascia in eredità ai suoi tre figli un enorme terreno di forma circolare, adattissimo per un'agricoltura di grande qualità. Egli, però, era un appassionato di problemi geometrici e pone dei vincoli pressanti all'eredità: i tre figli verranno in possesso di solo una parte del terreno. In particolare, solo di tre zone perfettamente ellittiche, contenute nel cerchio, che abbiano i seguenti requisiti:
(1) Le tre ellissi devono essere uguali tra loro.
(2) Le tre ellissi devono essere tangenti internamente alla circonferenza che delimita il campo.
(3) Le tre ellissi devono anche essere tangenti tra di loro.
I tre fratelli, amanti anch'essi della tradizione delle tavolette dipinte, descriventi problemi geometrici, che si ponevano nei templi (le Sangaku), riescono facilmente a risolvere il problema. Però, prima di portare la loro soluzione al notaio, ci riflettono per bene e si rendono conto che facendo un po' di conti possono risalire alle tre ellissi che, pur avendo i tre requisiti dati dal padre, abbiano anche l'area maggiore. In poche parole, riescono a sfruttare al massimo il campo.
Ponendo il raggio R del cerchio uguale a 1, quali sono i semiasse delle tre ellissi di massima area possibile?
La soluzione non è difficile, ma è necessario fare delle scelte "azzeccate" all'inizio e avere un po' di intuizione verso la fine.
QUI la soluzione
7 commenti
Provo a rispondere.
Semi-asse maggiore=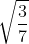
Semi-asse minore=
Calcolata supponendo che il posizionamento delle ellissi debba essere simmetrico ed il punto di tangenza con la circonferenza sia all'estremo del semiasse minore.
Il vincolo ulteriore è quello di avere le ellissi all'interno della circonferenza. Questo vincolo impone che la curvatura dell'ellisse nel punto di tangenza con la circonferenza sia al più uguale a quella della circonferenza.
caro Fabry... ma sei sicuro che sia quella di massima area? Penso ci sia bisogno di calcoli più generali...
Ho detto che ognuna delle tre ellissi deve essere tangente alla circonferenza, ma non ho detto quanti punti di tangenza abbia...
forza "geometri" ultra abili... date una mano a Fabry!!! impostato bene il problema (chiedete se non l'avete compreso bene...) diventa abbastanza semplice proseguire in modo "standard"...
Two is megl che one, come diceva la pubblicità.
Con un posizionamento simmetrico delle 3 ellissi e le ellissi ciascuna tangente a due punti della circonferenza, l'area più grande mi viene con semi-asse maggiore=1/√2 e semi-asse minore=1/√6.
Il procedimento che ho seguito richiede calcoli lunghi. Probabilmente non ho fatto le scelte giuste nella impostazione del problema.
Adesso sì che ti riconosco grande Fabry! Lasciamo pure da parte i conti, così magari qualcuno ci prova sapendo il risultato. Come dicevo, impostato bene l'inizio, tutto diventa abbastanza semplice anche se lungo e laborioso. Sarebbe bello anche vedere come varia l'area in funzione del semiasse... ma è inutile insistere...ù
Ecco la figura
Il valore del semiasse maggiore può essere nell'intervello![\left [ \sqrt{\frac{3}{7}},{\frac{\sqrt{3}}{2}} \right ]](http://latex.codecogs.com/gif.latex?\left&space;[&space;\sqrt{\frac{3}{7}},{\frac{\sqrt{3}}{2}}&space;\right&space;])
.
Sotto le ellissi non possono essere contemporaneamente tangenti tra loro e tangenti alla circonferenza.
Sopra non possono essere contenute nel cerchio senza sovrapporsi.