Questo è il dodicesimo articolo della serie "La Relatività Generale al microscopio"

Consideriamo uno spazio a due dimensioni in cui si traccino due assi non necessariamente perpendicolari tra di loro. Una coordinata la chiamiamo x^ν e l'altra x^μ, entrando finalmente nella terminologia, nel linguaggio matematico, usato da Einstein. Questi due indici stanno a indicare che possono rappresentare sia lo spazio, con le sue tre dimensioni, sia il tempo: la curvatura non è più solo spaziale, ma temporale, ricordando bene, tra le righe, il legame che esiste tra coordinate temporali e spaziali (Minkowski e l'invariante spaziotemporale insegnano). Un passo fondamentale, ciò che era solo spazio a n dimensioni diventa adesso, anche se non ci appaiono differenze visibili, uno spaziotempo con una coordinata decisamente particolare che va trattata sempre con le dovute precauzioni dato che è legata strettamente alle coordinate spaziali.

In questo sistema di riferimento disegniamo un banale parallelogramma che abbia due lati giacenti sugli assi e gli altri due a loro paralleli. Fig. 15.

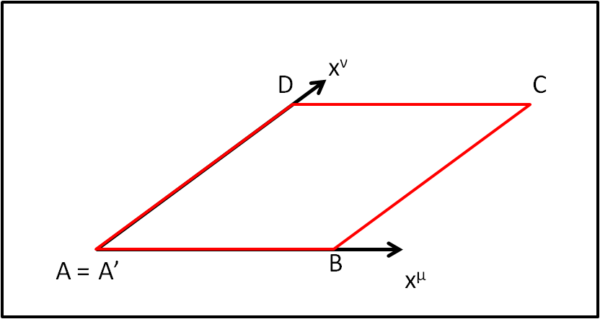
Indichiamo i 4 vertici con A, B, C e D. Applichiamo in A  un certo vettore VA (meglio non disegnarlo per non creare maggiore confusione, ma è facile immaginarlo) e poi facciamolo viaggiare lungo il parallelogramma con le modalità che abbiamo usato precedentemente. Quando giunge in B lo chiamiamo VB, poi VC , poi VD e infine nuovamente VA. Eh no! sarebbe troppo semplice... il nostro parallelogramma può essere comunque incurvato e quindi non è affatto detto che quando il vettore torna in A sia uguale a quello di partenza. Chiamiamo, allora, il punto di ritorno A', che coincide con A, ma al quale associamo il vettore VA'.

Eseguiamo qualche semplice differenza...

Confrontiamo, ad esempio, la differenza tra i vettori VC e VD con la differenza tra VB e VA, ossia scriviamo:

(VC - VD) - (VB - VA)

Ovviamente in uno spazio piano questa differenza è uguale a zero, ma in generale essa rappresenta la differenza lungo l'asse x^μ

Scriviamocelo per ricordarcelo

(VC - VD) - (VB - VA)                  differenza lungo x^μ

Analogamente possiamo considerare la differenza tra

(VC - VB) - (VD - VA')                 differenza lungo x^ν

Sottraiamo adesso la seconda differenza dalla prima:

(VC - VD) - (VB - VA) - ((VC - VB) - (VD - VA') )

VC - VD - VB + VA -VC +VB + VD - VA' =  VA - VA' = dV

VA - VA' non è altro che la differenza tra il vettore VA e lo stesso vettore VA' dopo  che ha fatto la sua passeggiata lungo il parallelogramma. Differenza che NON è assolutamente detto che sia  uguale a zero (in uno spazio curvo, come abbiamo dimostrato precedentemente). Il modulo del vettore rimane sempre uguale, ma non è assolutamente vero che sia zero l'angolo che essi formano tra di loro (nella superficie sferica abbiamo raggiunto anche 90 ° o addirittura 180°).

Analizziamo in modo più tecnico cosa sono le varie differenze utilizzate. Ad esempio, cosa rappresenta la differenza VC - VD? Nient'altro che la variazione del vettore V passando da D a C, ossia muovendosi di un intervallo lungo x^μ . In parole matematiche:

(VC - VD) = (∂V/∂x^μ)  dx^μ V

Attenzione: in uno spazio curvo lo spostamento di un vettore fa cambiare il sistema di riferimento e quindi è necessario introdurre la derivata covariante, ossia quella che corregge per la differenza della derivata di uno stesso vettore in sistemi diversi (il vettore è uguale, ma non la sua derivata normale, vedi simbolo di Christoffel). La relazione di prima deve essere scritta più correttamente:

(VC - VD) = ∇V_μ dx^μ V

Passiamo ora alla differenza (VB - VA). Anch'essa è una variazione del vettore lungo x^μ, per cui la differenza tra  (VC - VD) e (VB - VA) non è altro che un trasporto della differenza lungo x^ν, ossia  la derivata della differenza dei vettori fatta rispetto a x^ν. Derivata, ovviamente, covariante. Si può scrivere, perciò, come derivata covariante di una derivata covariante lungo una linea diversa (un trasporto lungo x^ν di una derivata (che è poi una differenza) su un'altra linea parallela ). Ossia dobbiamo eseguire una differenza di differenze. In parole matematiche, inserendo le derivate covarianti al posto delle "differenze", si  può scrivere

(VC - VD) - (VB - VA) = ∇V_ν dx^ν ∇V_μ dx^μ V

In modo del tutto analogo, invertendo dx^μ con dx^ν (lo spostamento lungo dx^ν viene spostato lungo  dx^μ )

(VC - VB) - (VD - VA') = ∇V_μ dx^μ  ∇V_ν  dx^ν V

Le derivate covarianti possono tranquillamente essere messe una di seguito all'altra (sono operazioni e l'importante è solo l'ordine con cui si svolgono) e scrivere:

(VC - VD) - (VB - VA) = ∇V_ν ∇V_μ dx^ν dx^μ V

(VC - VB) - (VD - VA') = ∇V_μ ∇V_ν dx^μ  dx^ν V

Non ci resta, allora, che fare la differenza tra le due e ottenere proprio dV (la differenza del vettore a fine percorso)

dV = ∇V_ν ∇V_μ dx^ν dx^μ V - ∇V_μ ∇V_ν dx^μ  dx^ν V

dx^ν e dx^μ sono intervalli e V è sempre lo stesso, per cui per loro non c'è problema di ordine

dV =  dx^μ dx^ν V (∇V_ν ∇V_μ  - ∇V_μ ∇V_ν)

Ma la parte segnata in rosso non è altro che la definizione di commutatore e, quindi, possiamo scriverlo come:

[∇V_ν ,∇V_μ]

Ricordiamoci, adesso, l'equazione (7) che diceva:

∇_nV_m =  ∂V_m(y)/∂yⁿ + Γ_mn^r V_r(x) 

Scriviamola utilizzando simboli più semplificati (ma l'equazione resta sempre la stessa):

∇_ν = ∂_ν + Γ_ν 

essa, in pratica, ci ricorda che la derivata covariante non è altro che la derivata "normale" più un termine aggiuntivo correttivo, proprio il simbolo di Christoffel. Possiamo utilizzare questa simbologia, sapendo che cosa rappresenta in realtà...

Il commutatore precedente può allora essere scritto:

[∂_ν + Γ_{ν ,} ∂_μ + Γ_μ ] = (∂_ν + Γ_ν)(∂_μ + Γ_μ ) - (∂_μ + Γ_μ )(∂_ν + Γ_ν)

svolgiamo il prodotto

∂_ν ∂_μ + ∂_ν Γ_μ  + Γ_ν ∂_μ + Γ_ν Γ_μ  - ∂_μ ∂_ν - ∂_μ Γ_ν - Γ_μ∂_ν  - Γ_μΓ_ν   

Raccogliamo meglio i termini, ricordando, però, che nelle derivate ordinarie l'ordine non ha alcuna importanza (lo stesso non vale per quelle covarianti!):

(∂_ν ∂_μ - ∂_μ ∂_ν) + (Γ_ν ∂_μ - ∂_μ Γ_ν)+ (∂_ν Γ_μ  - Γ_μ ∂_ν )+ (Γ_ν Γ_μ  - Γ_μ Γ_ν)

La parentesi rossa vale zero, per quanto appena detto sulle derivate ordinarie. Tutte le altre parentesi sono invece dei commutatori (AB - BA)

In particolare quello blu può essere scritto come:

- [∂_μ , Γ_ν]       (abbiamo invertito l'ordine e quindi posto un segno meno davanti: (AB - BA) = - (BA - AB)

Quello verde come:

[∂_ν , Γ_μ]

Quello arancione come:

[Γν, Γ_μ]

Ricordiamo, però, cosa avevamo dimostrato per il commutatore:

[∂/∂x, f(x)] = ∂f(x)/∂x

La blu e la verde diventano:

- [∂_μ , Γ_ν]  = - ∂Γ_ν/∂_μ

[∂_ν , Γ_μ] = ∂Γ_μ/∂_ν

Rimettiamo tutto assieme e definiamo il tensore di Ricci:

R_μν = [∇V_ν ,∇V_μ] = - ∂Γ_ν/∂_μ + ∂Γ_μ/∂_ν + [Γ_ν , Γ_μ]

da cui segue

dV = ∂x^μ ∂x^ν V R_μν

Ricordiamo che all'interno del tensore di Ricci, attraverso i simboli di Christoffel, compaiono sia il tensore metrico che la sua derivata. Detto in parole molto rozze, il tensore di Ricci misura la curvatura in relazione al percorso eseguito sullo spazio curvo. Esso è in grado di descrivere compiutamente, tenendo presente le correzioni eseguite per estrapolare il teorema di Pitagora (tensore metrico) e per sostituire le derivare ordinarie con quelle covarianti, la curvatura, qualsiasi essa sia. Non ci resta che capire di quale curvatura c'è bisogno, ma questo deve dircelo la parte "fisica", ossia la massa e, conseguentemente, l'energia sotto tutti i suoi aspetti.

I pennelli e i colori sono a posto, adesso bisogna realizzare praticamente  l'idea e lo spirito del capolavoro intellettuale. In pratica, la curvatura deve essere associata a qualcosa, un qualcosa che dice allo spaziotempo che tipo di curvatura deve assumere. A quel punto ne conseguiranno i movimenti della materia che si trova immersa in tale situazione GEOMETRICA. Lo so, sono solo belle parole, ma più di tanto non si riesce a fare senza utilizzare un linguaggio puramente matematico fuori dalla portata del nostro blog. Vedremo che proprio attraverso le leggi di Newton, più che accurate nelle condizioni in cui la curvatura è praticamente nulla, si potrà raggiungere una visione globale, senza alcun timore di avvicinarsi a masse (ed energie) di entità ben superiore. Cercherò di seguire un metodo molto semplificato, ma spero che sia sufficiente per far capire la vera opera d'arte.

RIFLESSIONE: è importantissimo stabilire molto bene, almeno concettualmente, quanto abbiamo fatto finora. Abbiamo usato vettori che si spostano secondo linee chiuse più o meno estese, abbiamo trasformato le loro coordinate in modo che certe caratteristiche essenziali non dipendano dal sistema di riferimento. Quando è stato necessario sono state eseguite e indicate molto bene le correzioni da apportare. Alla fine, si è definita e descritta perfettamente la geometria di uno spazio  (il tempo è per adesso una coordinata qualsiasi) a n dimensioni in ogni suo punto. L'importante è che ciò che è stato descritto sia del tutto invariante rispetto a qualsiasi cambiamento di sistema. Un lavoro di pura geometria, dove non esiste ancora nessun movimento. Abbiamo creato il campo di battaglia in cui si svolgeranno proprio i movimenti che, quindi dovranno tenerne conto.

E' venuta l'ora di vedere proprio questo... Iniziamo a far muovere le masse o quello che volete e vediamo come esse saranno soggette alle regole imposte dalla geometria del campo di battaglia. E' ora, quindi, di introdurre velocità e accelerazioni, ossia i veri movimenti che, come tali, vedono il tempo assumere un ruolo del tutto fondamentale. Basta ricordare che una velocità resta definita come uno spazio relativo a un tempo e che un'accelerazione è la variazione di questo parametro in funzione sempre del tempo. Possiamo già anticipare il procedimento da svolgere: la geometria curva, descritta in modo generale e invariante, dice alle masse come e dove possono muoversi, dato che sono legate alle regole dello spazio in cui vivono. Nello stesso momento, però, dovremo anche cercare di capire come fa una certa massa a costruire uno spazio così deformato.

Sappiamo trattare gli spazi curvi, ma adesso dobbiamo anche sapere con che tipo di spazio curvo abbiamo a che fare. Abbiamo imparato l'alfabeto della geometria spaziale, ma adesso dobbiamo scrivere un libro che voglia comunicare qualcosa, mantenendosi conforme alle lettere dell'alfabeto geometrico. Insomma, la massa dominante deve dire allo spazio quale forma deve ottenere... dobbiamo costruire il mollusco capace di assumere qualsiasi configurazione, tanto ormai sappiamo come descriverla senza alcuna paura del sistema di riferimento in cui vogliamo agire.