Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

 

Sintesi semplificata concettuale

Per chi non avesse voglia di seguire passo dopo passo la descrizione delle equazioni di Maxwell, riporto di seguito una breve sintesi del loro significato soprattutto fisico.

Come già detto, Maxwell unisce leggi già note e raffina l'ultima in modo da ottenere una perfetta simmetria tra campo elettrico e campo magnetico, tale da permettergli l'unificazione come campo elettromagnetico. La parola "unificazione" sta proprio a intendere che un campo non può fare a meno dell'altro, come un serpente che si morde la coda. Il campo si propaga attraverso onde (in ambito classico) che viaggiano alla velocità di circa 300 000 km/s.

Le prime due leggi, come vedremo tra poco, indicano una differenza tra i due campi basata sul fatto che una carica elettrica può esistere da sola (ad esempio un protone positivo e un elettrone negativo), mentre le cariche magnetiche (ad esempio, quelle di una normale calamita) non possono separarsi tra di loro: se la calamita viene "tagliata" in due si riformano immediatamente un polo positivo e uno negativo. Questa diversità tra i campi fa sì che nel caso di quello elettrico è sempre possibile costruire una superficie CHIUSA che contenga una certa carica, permettendo in tal modo di avere un campo elettrico che è solo uscente o entrante attraverso la superficie. Detto in parole tecniche questo significa che la divergenza del campo è sempre positiva o negativa. Se la superficie scelta non contiene cariche, tanto campo elettrico (meglio parlare di flusso, ossia campo per unità di superficie) entra e tanto ne esce. Tra poco dimostreremo questa asserzione attraverso una visuale molto schematica e attraverso la semplice matematica del teorema di Gauss.

Il campo magnetico, non potendo separare le due cariche, ossia non esistendo nessuna superficie CHIUSA in grado di contenerne una sola, è costretto ad avere sempre divergenza nulla, ossia tanto campo entra e tanto ne deve uscire.

Queste sono le prime due leggi che hanno proprio una semplicità innata dovuta alle caratteristiche stesse dei due campi.

A questo punto si fa un passo avanti e si dimostra che se si considera un filo in grado di trasportare una carica, la VARIAZIONE di un campo magnetico che lo influenzi, determina proprio lo scorrimento della carica. Dato che lo scorrimento di una carica implica la creazione di un campo elettrico, possiamo dire che la terza legge ci dice che variando il campo magnetico si crea un campo elettrico. Attenzione: il campo magnetico deve variare e non solo esistere e influenzare il filo!

La quarta legge è forse la più "complicata" anche se concettualmente molto semplice: così come la variazione di un campo magnetico crea un campo elettrico, così la VARIAZIONE di un campo elettrico crea un campo magnetico. In altre parole le loro variazioni sostengono a vicenda i due campi (essi diventano due facce della stessa medaglia). Il problema sorge solo nella descrizione di questa ultima legge, dato che si dimostra che il campo elettrico deve essere diviso in due parti entrambi capaci di creare un campo magnetico. Quest'ultimo passaggio dà la svolta storica alle leggi già esistenti e le completa in modo perfetto. Le quattro relazioni danno luogo matematicamente a delle equazioni differenziali  (ricordatevi il moto di un pianeta attorno al Sole ottenuto dall'equazione differenziale di Newton), la cui soluzione porta proprio a una radiazione che oscilla sia nel tempo che nello spazio, ossia alle onde elettromagnetiche.

Questo brevissimo riassunto ha fatto uso di "termini" non sempre corretti, ma penso che riesca a dare una visione concettuale d'insieme. Ora saliamo di un piccolo gradino e studiamo più da vicino le prime due ancora in modo semplificato. Poi, entreremo decisamente in un ambito più matematico, senza, però, averne paura. Troveremo molti integrali, ma la maggior parte di loro starà solo a indicare che quello che capita in un certo segmento, superficie o volume piccolissimo viene esteso a tutto un cerchio o a una superficie chiusa o al volume che essa contiene. Saranno solo e soltanto delle somme di tante piccoli "frammenti" necessari per descrivere la struttura finale.

In questo contesto, eseguendo queste somme e quindi lavorando su strutture di grandezza qualsiasi siamo obbligati a passare attraverso gli integrali (versione integrale), se invece restiamo in ambito del singolo pezzetto infinitesimo ricadiamo nella versione differenziale. Solo in quest'ultima, dovendo applicare i vettori punto per punto, vi è la necessità di introdurre gli operatori divergenza e , soprattutto, rotore. La divergenza può essere applicata a uno scalare e quindi facilmente trasferibile da una visione all'altra. La variazione del vettore campo introduce invece delle derivate (chiamatele pure -se volete- velocità), da cui la comodità di un operatore che sappia lavorare punto per punto su coppie di vettori e produrne un terzo (rotore). Niente a che vedere con i tensori, ma in qualche modo la strategia non è molto diversa da quella che ci ha accompagnato, in modo più complesso, nella relatività generale.

N.B.: Troverete molti concetti ripetuti fino alla nausea, ma penso che sia importante avere sempre sottomano le formule già descritte. Al limite, quando l'intera trattazione sarà terminata (con molta calma), si potrà eliminare qualche ripetizione...

Campo elettrico

Abbiamo definito gli operatori div e rot, qualsiasi sia il campo vettoriale che si potrebbe scegliere. A questo punto ne scegliamo uno in modo specifico e vediamo, innanzitutto, che cosa comportano gli operatori su questo particolare campo.

Beh... non vi stupirete di certo se vi dico che scegliamo il campo elettrico E. Lo definiremo molto meglio nei capitoli successivi, ma, per adesso pensiamo a un campo in cui sono presenti due punti molto particolari. Uno è dato da una carica elettrica POSITIVA e uno da una carica elettrica NEGATIVA (in poche parole, potremmo  scegliere un protone e un elettrone). Sappiamo molto bene che questo campo può essere descritto da vettori che escono dalla carica positiva e che entrano nella carica negativa. In fondo, nei dintorni della carica negativa, siamo di fronte a qualcosa di molto simile al campo gravitazionale.

Disegniamolo in modo molto approssimato in Fig. 4. O, se preferite, potete anche immaginarvi una vasca da bagno, in cui da un lato c'è un rubinetto e dall'altro uno scarico. Rubinetto e scarico sono regolati in modo che tutta l'acqua che esce dal primo viene  fatta sparire dal secondo (insomma, non si rischiano inondazioni...).

Bene, vediamo un po' cosa succede ai nostri operatori, in particolare alla divergenza...

Poniamoci tra le due cariche e scegliamo il nostro volumetto. Beh... siamo proprio nel caso dell'acqua che scorre e che è incomprimibile: tanti vettori entrano  e tanti vettori escono. Possiamo anche parlare di flusso (campo vettoriale per superficie), allargando un pochino il nostro volumetto: il flusso in entrata è uguale al flusso in uscita. Sicuramente siamo di fronte a una divergenza uguale a ZERO.

Spostiamo, adesso il nostro volumetto in una posizione molto particolare, ossia quella che contiene la carica positiva o quella negativa. Ci conviene fare uno zoom nell'intorno di questi punti per capire ancora meglio il campo vettoriale. Esso, infatti, ha un'altra caratteristica che lo rende simile alla gravitazione. Il campo diminuisce di intensità allontanandosi dalla carica.

Consideriamo perciò la Fig. 5, dove in (a) esce il campo e in (b) entra.

I due volumetti che contengono le cariche ci dicono subito una cosa veramente ovvia. In quello "positivo" il campo vettoriale ESCE soltanto dal volumetto (dobbiamo sempre considerare le sue facce esterne, ovviamente). Ne segue che la divergenza è sicuramente positiva. Nel volumetto "negativo", invece, il campo entra soltanto e, quindi la divergenza è sicuramente NEGATIVA.

Per non fare confusione, è sempre meglio immaginare cosa capita nei dintorni di una carica, in modo che il campo si mostri nella sua vera essenza.

A questo punto casca l'asino... prendiamo un volumetto abbastanza vicino alla carica in cui entra il campo, ma che non la contenga. Tenendo conto che i vettori calano d'intensità allontanandosi dalla carica potremmo concludere che anche in quel  caso la divergenza dovrebbe essere positiva, ossia il flusso che esce dovrebbe essere maggiore di quello che entra...

Eh no, amici miei! Basta ricordare il paradosso di Olbers (dove c'entra proprio il teorema di Gauss) e ricordare che il campo diminuisce al crescere del quadrato della distanza, ma anche che la superficie che emette cresce con il quadrato della distanza. I due effetti si eliminano e possiamo concludere che il cielo, indipendentemente dalla distanza di una superficie sferica da noi, emette sempre la stessa quantità di luce. In parole povere, più vicini siamo è maggiore è la luce emessa, ma le stelle sono di meno. Su una superficie di raggio maggiore la luce è più debole, ma le stelle sono molte di più.

Facciamo un esempio molto rozzo in Fig. 6 (guardatelo e poi dimenticatelo, mi raccomando!): inseriamo il nostro cubetto (che possiamo disegnare come un quadratino), all'interno del campo che sta dirigendosi verso la carica, Bene, dal lato più vicino alla carica inferiore esce un flusso maggiore, ma il flusso che entra coinvolge sia la faccia più lontana, sia quelle laterali... alla fine tanto ne entra e tanto ne esce!

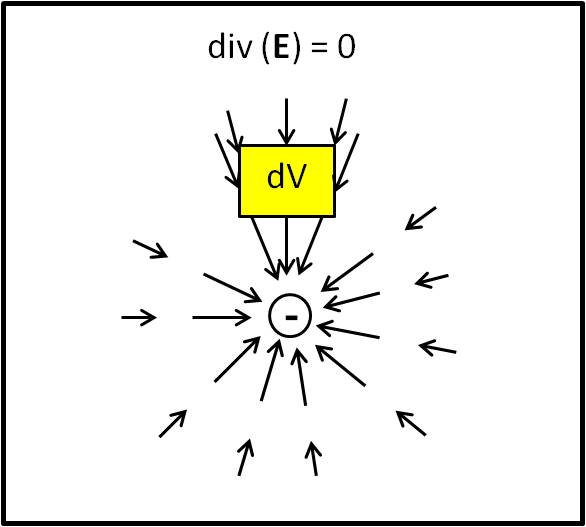
In parole molto sintetiche: Il flusso entrante e uscente da un volumetto dV è sempre lo stesso, a meno che non contenga una carica. Ossia la divergenza è sempre zero tranne che nei volumetti che contengono la carica.

N.B.: Per non venire linciato dai più esperti, in appendice riporto la dimostrazione seria del teorema di Gauss.

Campo magnetico

Bene, abbiamo visto che la divergenza è sempre zero, tranne che quando contiene la carica. Cambiamo, adesso.  "leggermente" il campo e prendiamo quello magnetico, chiamandolo B.

Pensiamo alla Terra con il suo Polo Nord e il suo Polo Sud (magnetici si intende), ma è ancora meglio pensare a un piccolo dipolo magnetico (una normale calamita). Le linee del campo con i rispettivi vettori escono da un polo ed entrano nell'altro (Fig. 7). Sembra di essere nelle stesse condizioni del caso precedente. Infatti, la divergenza è sempre uguale a zero, tanto flusso esce e tanto flusso entra.

Non ci resta che provare a inserire all'interno del volumetto la carica! Risulta un po' difficile, dato che il volumetto deve contenere parte della calamita. Poco male, tagliamo la calamita in modo da inserire solo il polo nord o il polo sud, da cui esce o entra il campo (Fig.8).

Accidenti! Nei due pezzetti ottenuti  si è formato immediatamente un polo sud e un polo nord. I due poli sembrano proprio non volersi mai staccare tra loro. E più cerco di considerarne uno solo e più piccola si fa la calamita. A parte gli scherzi, in un dipolo magnetico, quello che causa un campo vettoriale magnetico, una carica da sola non può esistere. In termini "tecnici" ciò vuol dire che non esiste un MONOPOLO magnetico e che, quindi, qualsiasi sia il cubetto che viene considerato vi sarà sempre tanto campo che entra e tanto che esce. Possiamo concludere che la divergenza del campo magnetico è sempre zero.

Ridendo e scherzando abbiamo già descritto le prime due leggi di Maxwell: la prima ci dice che in un campo elettrico la divergenza che contiene una carica positiva è sempre POSITIVA e vale un qualcosa che dipende ovviamente dalla carica contenuta. La secondaci dice che la divergenza di un campo magnetico è sempre uguale a zero.

Se chiamiamo il campo elettrico E e quello magnetico B, possiamo scrivere

div(E) = kQ         (dove Q è la carica)

div(B) = 0

Dovremmo parlare adesso dei rotori... ma è meglio soprassedere, dato che questo tipo di operatore entra in modo un po' più complesso nell'intera faccenda.  Per adesso ci basti ricordare che il rotore è un qualcosa che risulta ORTOGONALE a un certo piano individuato da due vettori, di cui uno è proprio il campo considerato. La faccenda diventa giocoforza tridimensionale. Le ultime due leggi di Maxwell li introducono, ma  introducono anche le variazioni dei campi in funzione del  tempo. Queste variazioni riescono a mostrare che quella del campo magnetico induce un campo elettrico e viceversa. Un vero legame di sangue tra i due campi  che sono capaci di crearsi reciprocamente se smettono di essere "statici" e  iniziano a variare "dinamicamente".

E' ora di entrare con la dovuta calma e attenzione nella quantificazione delle leggi, utilizzando per adesso la versione integrale.

 

Appendice: Il teorema di Gauss

Consideriamo un campo elettrico (la carica sia positiva, Q) e una sfera in esso immersa, che non contenga cariche. Vediamo di calcolarne il flusso entrante e uscente.

Innanzitutto dobbiamo ricordare una proprietà dell'angolo solido α: se dS₁ e dS₂ sono le aree della superficie sferica superficie sferica corrispondenti all' angolo solido (Fig. 9) si può scrivere che:

dS₁/R₁² = dS₂/R₂² = α

dove R₁ e R₂ sono le distanze dall'origine del campo.

Tuttavia sappiamo anche che la divergenza è data dalla somma dei prodotti scalari tra i vettori di modulo dS uscenti dalle due superfici e i vettore del campo corrispondenti (questo prodotto è proprio il flusso. Nell'articolo precedente, avevamo considerato aree unitarie e quindi solo i versori). Si ha quindi:

div(F₁) = - F₁ x dS₁ = - F₁ dS₁

div(F₂) = F₂ x dS2 = F₂ dS₂

Non dimentichiamoci, però, che il campo elettrico (così come quello gravitazionale) diminuisce con il quadrato della distanza R, ossia:

F₁ = k/R₁²

F2 = k/R₂²

Sostituendo abbiamo che.

div(F₁) = - (k/R₁²)dS₁

div(F₂) = (k/R₂²)dS₂

Tuttavia, sappiamo che

dS₁/R₁² = dS₂/R₂² = α

Da cui:

div(F₁) = - k α

div(F₂) = k α

Sommando si ha proprio:

div(F) = 0

Ovviamente, lo stesso risultato si ha per ogni angolo solido, per cui nella sfera iniziale tanto campo entra e tanto campo esce.