Categorie: Matematica
Tags: dimensioni parallelepipedo quiz scatole volume
Scritto da: Vincenzo Zappalà
Commenti:12
Le due scatole: un quiz per tutti *
Anna e Bruno devono costruire due scatole che contengano i loro regali per i genitori. Alla fine, le due scatole sembrano quasi uguali, ma non lo sono realmente...
La scatola di Anna ha la forma di un parallelepipedo e le sue dimensioni sono quelle indicate nella Fig. 1
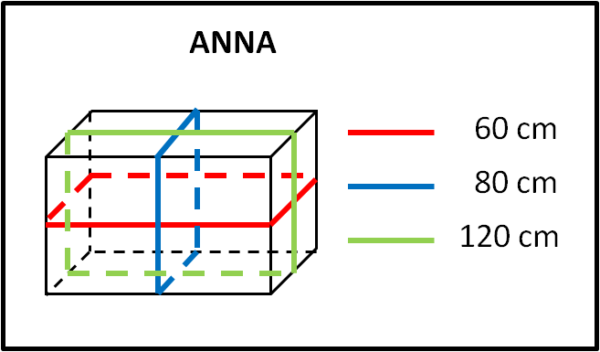
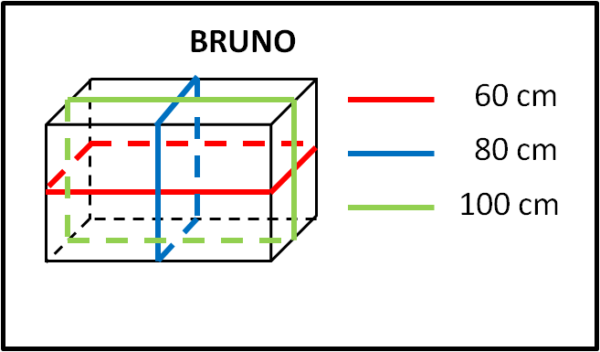
La scatola di Bruno ha anch'essa la forma di un parallelepipedo, ma la misura della terza dimensione è minore di quella di Anna, come mostra la Fig. 2
Si chiede:
Di quanto il volume della scatola di Anna supera il volume della scatola di Bruno?
N.B.: i più bravi si astengano per qualche giorno. Grazie!






12 commenti
Beh?! Non vi piacciono più i quiz? Via libera anche ai più bravi!!!
La differenza è data da una fetta di parallelepipedo, anch'essa a forma di parallelepipedo, le cui misure sono 60 cm * 80 cm * 20 cm = 96000 cm3 = 96 dm3
Il medesimo risultato si ottiene, naturalmente, facendo la differenza tra il volume delle due scatole: 60 * 80 * 120 - 60 * 80 * 100 = 60 * 80 * (120 - 100) = 60 * 80 * 20 = 96000
caro Marco,
tu dici che la scatola di Anna supera, in volume, quella di Bruno della quantità che hai riportato? Potresti darmi i volumi delle due scatole? Temo che ci sia qualcosa che non va... potrei sbagliarmi o non ho capito bene... Fai attenzione alla figura per calcolare il volume!
Ach: non mi sono reso conto che le tre misure sono i perimetri delle facce del parallelepipedo !! In effetti mi sembrava un po' troppo facile !!
Più tardi (ora sto lavorando) ci torno sopra ...
1.625 cm3
caro Agapito,
mi stai dicendo che quella di Anna ha un volume maggiore di quella di Bruno di 1625 cm3?
No. Per non togliere il divertimento ad altri ho postato solo il risultato in valore assoluto e neanche il procedimento.
grazie Agapito
Rifatto rimediando all'abbaglio di ieri: Bruno > Anna di 1625 cm3
Siano a1, a2 e a3 le dimensioni della scatola di Anna. Sappiamo che:
2.a1+2.a3=60
2.a2+2.a3=80
2.a1+2.a2=120
Si può quindi determinare facilmente che:
a1= (60-2.a3)/2 --> 30-a3
a2=(80-2.a3)/2 --> 40-a3
Di conseguenza, si ha, sostituendo a1 e a2 nel terzo perimetro, che:
60-2.a3 + 80-2.a3 = 120, da cui 4.a3=140-120 --> a3=5.
Sostituisco ora il valore di a3 in uno dei due perimetri ove compare, per esempio il primo:
2.a1+ 2.5=60 --> a1=(60-10)/2=25
Quindi, analogamente a2=(80-2.5)/2=35
Il volume della scatola di Anna è 25 x 35 x 5 = 4.375 cm3.
Procedendo in maniera del tutto analoga per la scatola di Bruno, si trova che le dimensioni della sua scatola sono: b1=20; b2=30; b3=10, e quindi il volume della scatola di Bruno è 20 x 30 x 10 = 6.000 cm3, quindi la scatola di Bruno è più grande di 6.000-4.375=1.625 cm3 rispetto a quella di Anna.
perfetto ragazzi!!!