Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

Campo magnetico: due poli inseparabili   

Non ci resta che ripetere l'esercizio con  un campo magnetico. Tutto sembrerebbe andare di comune accordo. Consideriamo un polo magnetico M, da cui fuoriesce (o entra) un certo campo che ha come vettore B e non E, e riscriviamo il risultato precedente:

Φ_B = ∫B x dA = M/k

Abbiamo solo cambiato la costante dato che è molto facile che non sia la stessa del campo elettrico... Perfetto? Neanche per sogno... o, almeno, il risultato finale è costretto a dirci che M = 0. Ma come? Abbiamo preso una sfera attorno a un polo magnetico, che sembra comportarsi esattamente come una carica elettrica. Eh no! amici miei. Se immaginiamo di inserire un piccolo magnete all'interno della sfera, il polo negativo viene trascinato insieme a quello positivo. E' come se dentro la sfera vi fosse una carica positiva e una negativa. I due poli magnetici, come già accennato precedentemente sono INDIVISIBILI. Dobbiamo, quindi, scrivere, sempre e comunque che:

Φ_B = ∫B x dA = 0

E questa è la seconda equazione di Maxwell.

Essa ci dice che il flusso magnetico uscente da una superficie che contiene un dipolo è sempre UGUALE a zero, ossia la divergenza è zero!  Da una parte della sfera avremmo un flusso uscente, ma dall'altra parte avremmo un flusso entrante. Sommandoli essi si eliderebbero completamente: niente esce e niente entra.

Noi, da bravi italiani, potremmo cercare di fare i furbi e inserire il dipolo magnetico come mostrato in Fig. 11bis.

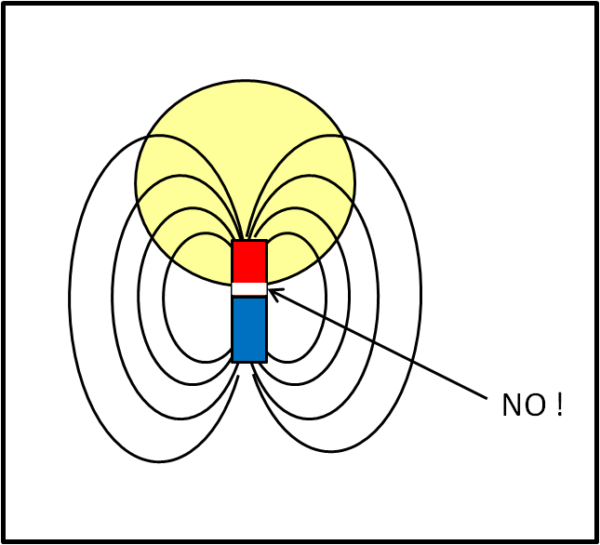
No, no, niente da fare, dato che facendo così violeremmo una delle ipotesi di partenza: la sfera deve contenere la carica e deve essere una superficie CHIUSA. E questa ipotesi non sarebbe valida perché la sfera attraverserebbe il dipolo e non sarebbe veramente chiusa. Beh... si potrebbe tagliare il dipolo in modo da far passare la sfera... Eh no! Facendo in questo modo si creerebbe immediatamente un nuovo polo in grado di bilanciare esattamente quello già immerso nella sfera. Niente da fare, in un dipolo magnetico, almeno per quanto ne sappiamo oggi, i due poli non possono essere mai separati. Ripetiamo, ancora, NON ESISTE un monopolo magnetico!

In realtà, una cosa analoga succederebbe se prendessimo una sfera del tutto esterna al dipolo. In questo caso succederebbe come già dimostrato per il campo elettrico: il flusso entrante sarebbe sempre uguale al flusso uscente (la divergenza sarebbe sempre zero).

Attenzione: questo non vuol dire assolutamente che non esiste campo magnetico, ma solo e soltanto che qualsiasi superficie chiusa contenente oppure no il dipolo magnetico  ha sempre parità tra flusso entrante e flusso uscente.

continua ...