Questo articolo è inserito nella sezione d'archivio dedicata all'Elettromagnetismo

 

Facciamo partire l'orologio

Le cose, adesso, cominciano a complicarsi leggermente. Finora abbiamo considerato una situazione statica, ossia abbiamo analizzato i campi bloccando il nostro orologio. Sappiamo che i vettori del campo implicano un movimento delle cariche inserite al loro interno, ma fermando il tempo non abbiamo ancora fatto muovere la carica e quindi non abbiamo ancora analizzato le variazioni del campo con il tempo.

Per analogia con il campo gravitazionale, è come se mettessimo una piccola massa a una certa distanza dalla Terra e fermassimo il tempo: la vedremmo immobile (il movimento ha bisogno di legare una variazione di spazio a una variazione del tempo...). A qualsiasi distanza la mettessimo, avremmo tante belle piccole masse in attesa di sapere cosa fare. Ci limiteremmo a dire che quelle più lontane subiscono un campo minore di quelle più vicine. Ben altro spettacolo avremmo se facessimo partire il nostro orologio: improvvisamente le piccole masse cadrebbero verso la Terra, come una pioggia e vedremmo anche che esse seguono movimenti diversi, dato che nello stesso intervallo di tempo descrivono spazi diversi (attenzione: stiamo vedendo le cose secondo la teoria newtoniana!). In poche parole le particelle o le cariche acquistano una certa velocità che, però, non è costante a causa delle caratteristiche del campo.

In particolare, quando abbiamo due campi, uno elettrico e uno magnetico, la faccenda si complica (fortunatamente) e i due campi, che possono finalmente agire praticamente sulle cariche, mettendole in moto, s'influenzano l'uno con l'altro. Entriamo in un mondo veramente nuovo, già compreso da Faraday, ma non ancora intrecciato in modo perfetto.

Bando alle ciance e via con la ricerca della terza equazione.

Consideriamo un "filo conduttore" che si chiuda su stesso; in parole tecniche un filo che permetta il passaggio di cariche elettriche lungo tutta la sua linea. Se il materiale è quello giusto, sappiamo benissimo che questo risultato si può ottenere creando una differenza di potenziale (ci torneremo tra poco) tra un capo e l'altro del filo. Gli elettroni cominceranno a girare lungo il filo elettrico, portando una corrente I. Questo scenario apre il mondo dell'elettricità che, al momento almeno, dobbiamo prendere per buona, altrimenti saremmo costretti a scrivere un libro intero di Fisica II o giù di lì.

Cerchiamo, perciò. di prendere alcune concetti per buoni (al limite, li spiegheremo in modo molto terra-terra). L'importante è ricordare che la corrente elettrica non è altro che un movimento di elettroni che lasciano il polo negativo per andare verso il polo positivo.  Per ottenere questo movimento solitamente si inserisce una "batteria" per creare i due poli e una resistenza per rallentare il moto degli elettroni. Poco importa a noi, adesso, dato che non vogliamo usare né batterie ne resistenza. Consideriamo solo un filo potenzialmente in grado di fare da autostrada agli elettroni.

Prendiamo, ora, un dipolo magnetico, con i suoi due poli inseparabili e inseriamolo all'interno del nostro filo circolare. Sembra che non capiti niente e... invece, basta che lo si allontani o lo si avvicini al nostro cerchio ed ecco che improvvisamente gli elettroni del filo cominciano a muoversi. In parole estremamente banali la variazione del campo magnetico induce una corrente elettrica I nel filo circolare. Se non muovessimo il dipolo non succederebbe niente, ma, muovendolo, ossia facendolo variare nello spazio relativamente al circuito elettrico (chiamiamo così il nostro filo circolare), si crea  una corrente elettrica I. Non solo però: se il magnete si muove in un verso , la corrente I circola in un senso, se il magnete inverte il moto, lo stesso deve fa la corrente. In particolare, se il magnete entra all'interno del circuito disegnato su un foglio, la corrente (ossia gli elettroni) circola in senso orario; se il magnete esce si inverte il verso.

Fatemi fare un esempio che verrà utilissimo... immaginiamo di voler introdurre una vite all'interno del cerchio: se la vite vuole entrare è necessario che giri in senso orario. Se vogliamo toglierla dobbiamo girare in senso antiorario. Sintetizzando, una vite che entra causa una rotazione oraria e una che esce una rotazione antioraria. Qualcosa che non può non ricordarci il prodotto vettoriale o la regola della mano destra. Qualsiasi riferimento all'operatore ROTORE non è per niente casuale.

Torniamo a una trattazione più rigorosa, ma già con l'idea finale in testa...

Campo elettrico indotto da un campo magnetico

Come già accennato, la capacità di muovere una carica lungo il filo è legata, ovviamente, alla differenza di potenziale tra i due capi del filo. Non è una vera forza, ma chiamiamola, per adesso, forza elettromotrice (FEM), un qualcosa che permette lo scorrimento delle cariche. Nel nostro caso non usiamo batterie ma solo e soltanto il campo magnetico e, in particolare, il suoi movimenti. Si è determinato sperimentalmente che la forza elettromotrice è proporzionale alla variazione del campo magnetico e all'area contenuta nel cerchio di filo (chiamiamola A); in altre parole, è uguale alla variazione del flusso:

La variazione del campo magnetico possiamo scriverla come

dB/dt

A noi interessa anche sapere quanto campo entra nell'area. Calcolo ovvio e grandezza già introdotta, ossia il flusso

dΦ_B = B x dA

Che esteso a tutta l'area diventa

Φ_B = ∫B x dA

Possiamo perciò derivare rispetto al tempo e uguagliare alla FEM.

FEM = d∫(B x dA)/dt  = dΦ_B /dt        .... (1)

In pratica, invece di creare una differenza di potenziale, otteniamo una circuitazione di corrente sul filo agendo solo sulla variazione del campo magnetico estesa a tutta l'area racchiusa all'interno del filo.

Non compare ancora il campo elettrico E, ma siamo molto vicini alla terza equazione. Lasciamo per un po' questa relazione in attesa e vediamo di fare intervenire non la corrente, ma il campo elettrico legato al filo percorso da corrente.

Consideriamo due piastre  su cui è spalmata una carica; una piastra ha carica positiva e una negativa. Introduciamo, per semplicità, la carica per unità di area (densità di carica) e la chiamiamo ρ, ossia

ρ = Q/A

o, più intuitivamente

Q = ρ A

essa ci dice come è distribuita la carica sull'intera area, così come la "normale" densità ci dice come è distribuita la massa su un certo volume. Se la densità è costante la massa è distribuita in modo uniforme; se la densità di carica è costante vuol dire che la carica è distribuita in modo uniforme sulla piastra.

Per il momento, consideriamo solo una piastra P (Fig. 12 ).

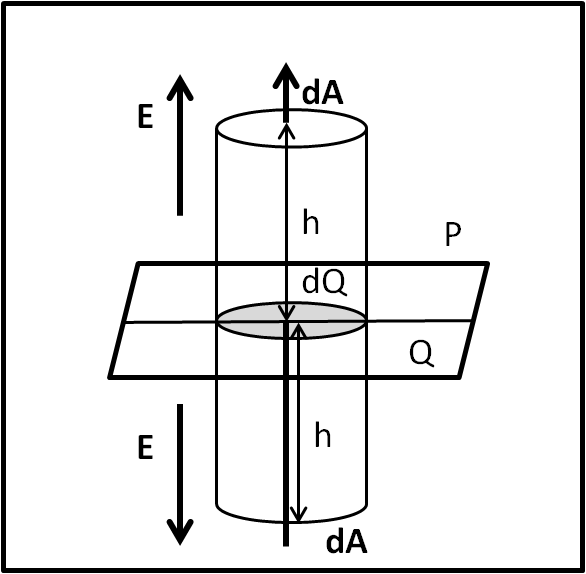
Prendiamo un area circolare su di essa e costruiamo un cilindro che vada verso l'alto e verso il basso. La carica presente sulla piccola area della piastra origina un campo elettrico che va sia verso l'alto che verso il basso. Dato che la carica è la stessa, il vettore campo sarà uguale in entrambe le direzioni. Blocchiamo il nostro cilindro a una certa altezza h, sia sopra che sotto. Ovviamente, la piastra è divisa in tante piccole aree e tanti cilindri tutti uguali tra loro. Tuttavia, l'unica componente del campo che contribuisce al flusso  è quella perpendicolare alla piccola area della piastra. Infatti ci ricordiamo molto bene che il flusso è dato da un prodotto scalare tra vettore e versore perpendicolare all'area, o -ancora meglio- tra vettore campo e vettore di modulo dA perpendicolare all'area dA.

Scriviamo la ormai ben nota relazione tra flusso e carica elettrica

E x dA = dQ/ε₀

Dato che i vettori del prodotto scalare sono paralleli, possiamo tranquillamente usare i moduli dei vettori

E dA = dQ/ε₀

Praticamente possiamo dire che l'unico flusso presente è quello che esce dalle superfici circolari dei cilindri.

Le nostre aree sono le aree di cerchietti, per cui  il flusso esce sia dal cerchietto posto in basso, a distanza h dalla piastra, sia da quello posto in alto. Ossia l'area di uscita del flusso è data dal DOPPIO dell'area del cerchietto (in breve, 2dA)

2E dA = dQ/ε₀ = ρ dA/ε₀

Al posto della carica presente sulla piastra abbiamo inserito la densità di carica moltiplicata per l'area del cerchietto della piastra.

Semplificando, abbiamo:

2 E = ρ/ε₀

E = ρ/2ε₀

Questa relazione, derivata in modo estremamente elementare, è di enorme importanza, in quanto ci dice che il campo elettrico NON DIPENDE assolutamente dall'altezza h del cilindro: esso è sempre lo stesso a qualsiasi distanza lo si consideri.

E' ora di introdurre la seconda piastra... ma il gioco è ormai quasi ovvio.

Se nella prima piastra la carica era positiva, nella seconda essa deve essere negativa (o viceversa). Consideriamo positiva quella superiore. Il vettore del corrispondente campo E non varia con la distanza ed è sempre uscente dalla piastra (Fig. 13, in cui le piastre sono disegnate "di taglio").

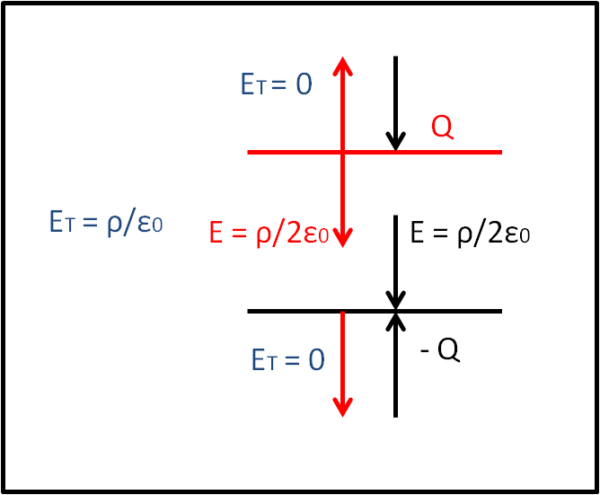
In particolare, esso è diretto verso l'alto, e verso il basso, indipendentemente dal fatto che esista una seconda piastra. La stessa cosa, però capita alla seconda piastra, che ha carica negativa e quindi vede il vettore campo andare verso la piastra, con lo stesso modulo della piastra superiore ma in verso opposto.

E' immediato concludere che il campo totale E_T esterno alle piastre si deve annullare, dato che i vettori sono uguali e di verso opposto, mentre, invece, quelli tra le due piastre si devono sommare e il verso è ovviamente quello che va dalla carica positiva verso la carica negativa (come già stabilito precedentemente).

Concludendo, all'esterno delle piastre in campo è uguale a zero, mentre all'interno delle piastre il campo è dato dal doppio  del valore ricavato dalla singola piastra, ossia:

E = 2 (ρ/(2 ε₀))

E = ρ/ε₀

Coloro che masticano un po' di elettricità "pratica" hanno già capito che abbiamo descritto un condensatore, un sistema che sfrutta proprio il fatto che se due piastre caricate di segno opposto sono tenute a una certa distanza e separate da un mezzo che non conduce corrente permettono di immagazzinare energia.

Non ci resta, ora, che introdurre il voltaggio. Che cosa rappresenta? Una differenza di energia potenziale capace di far muovere una carica elettrica da un punto a un altro. Più tecnicamente, possiamo  dire che il voltaggio è il lavoro svolto per portare una piccola carica q dall'infinito fino a una certa distanza r dalla carica Q (ci ricorda perfettamente l'energia potenziale gravitazionale). In altre parole, diventa il potenziale elettrico per unità di carica. Ricordiamo la definizione di energia potenziale. Essa è data dal lavoro fatto, ossia dalla forza agente moltiplicata per la distanza:

E_P = F_C  r

Qual è l'energia potenziale all'infinito? Beh... sicuramente ZERO, dato che r è proprio uguale a infinito e la forza F_C ( la forza di Coulomb) è data da:

F = q Q/(ε₀ 4πr²)

Ma r è infinito e quindi la forza è zero.

A una distanza r l'energia potenziale è data da una forza non nulla moltiplicata per la distanza, ossia:

E_P =  r q Q/(ε₀ 4πr²)

E_P =  q Q/(ε₀ 4πr)

Abbiamo appena detto che il voltaggio V è proprio l'energia potenziale per unità di carica e quindi basta dividere la relazione appena scritta per q e abbiamo:

V = Q/(ε₀ 4πr)

Tuttavia, ricordiamoci quanto valeva il campo elettrico:

E = Q/(ε₀ 4πr²)

per cui:

E = V/r

Torniamo alle nostre piastre di carica opposta. Tra di loro vi deve essere una differenza di  voltaggio e possiamo porre quello della piastra superiore come V e quello della piastra inferiore come 0. Tra esse vi è un campo elettrico che è, per quanto appena dimostrato, sempre uguale. Il campo è uguale, ma non la differenza di voltaggio, il quale dipende dal punto considerato tra le due piastre. Se ci mettessimo esattamente a metà il voltaggio sarebbe uguale a V/2. D'altra parte sappiamo che

V = E r

e se E rimane costante, al variare di r deve variare anche V.

trasportiamo, adesso, le nostre piastre (in modo virtuale) sul famoso cerchio di filo, come mostrato in Fig. 14 (in pratica, immaginiamo di tagliare il filo e separarlo di dl).

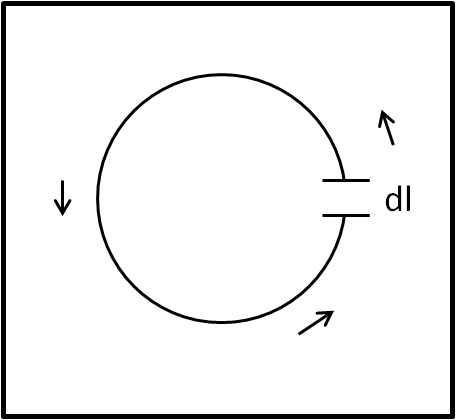
Tra le due "piastre" virtuali si ripete la situazione appena descritta. In altre parole è come se interrompessimo il filo, dato che siamo interessati al valore del campo elettrico indotto.  Ricordiamoci, però, come avevamo descritto la forza elettromotrice, che non era una vera forza, ma proprio il voltaggio, che adesso vale:

FEM = V = E dl

Anzi, per essere corretti è meglio usare il prodotto scalare:

FEM = V = E x dl

A questo punto per avere la FEM totale basta integrare lungo il filo (in gergo facciamo una circuitazione):

FEM = ∫E x dl

E' giunto il momento di completare la formula (1) che avevamo lasciato in sospeso

FEM = dΦ_B /dt = d∫(B x dA)/dt  = ∫E x dl

 ∫E x dl = dΦ_B /dt = d∫(B x dA)/dt

La formula ci dice che la variazione del campo magnetico rispetto al tempo induce una corrente sul filo e, di conseguenza, un campo elettrico.

Attenzione: tagliando virtualmente il filo lungo tutto il circuito abbiamo dimostrato che la corrente genera un campo elettrico o, ancora meglio, che oltre al passaggio di corrente abbiamo un campo elettrico. Questa conclusione sarà fondamentale per la quarta legge che Maxwell riuscirà a rendere perfettamente simmetrica alla terza equazione.

Questa è la terza equazione detta anche Legge di Faraday. Il succo fondamentale è proprio quanto già delineato a grandi linee: la variazione di un campo magnetico induce un campo elettrico o -se preferiamo- una corrente elettrica su un filo circolare, senza dimenticare che la corrente impone l'esistenza di un campo elettrico.

N.B.: Non gridate all'errore. Normalmente  si trova il segno meno a destra dell'uguale perché si considera il campo col verso opposto, ossia si considera il movimento delle cariche negative (gli elettroni). Eseguiamo pure questo cambiamento di segno...

 ∫E x dl = - d∫(B x dA)/dt

Affrontiamo ora la parte forse più complicata, ma quella in cui il genio di Maxwell si esprime al meglio dato che riesce a completare uno scambio di favori reciproco e perfettamente simmetrico: la strada per un unico campo elettromagnetico si sta aprendo completamente.

Continua ...