Questo articolo è inserito in Relatività Generale e tra le Ciliegine Cosmiche

 

Se mando un segnale su Venere, posizionato dalla parte opposta del Sole rispetto alla Terra, e aspetto che torni indietro, mi accorgerò che il tempo impiegato è maggiore di quello calcolato teoricamente. Come mai? Basta tener presente che la luce è dovuta transitare due volte nei pressi del Sole... Ciò vuol forse dire che la velocità della luce è diminuita? Chiedetelo a Shapiro.

Le prove sperimentali della correttezza della Relatività Generale sono aumentate col passare degli anni, portando recentemente a quella fantastica, relativa all'emissione di onde gravitazionali. Quelle più antiche, che avevano finalmente distrutto la diffidenza verso la nuova rivoluzionaria teoria sono però solo tre, dette proprio "classiche": la deflessione della luce che passa vicino a un corpo massiccio, il redshift gravitazionale e la precessione del perielio di Mercurio. Le prime due le abbiamo già trattate esaurientemente in vari articoli, mentre per quella relativa alla precessione del perielio di Mercurio i calcoli necessari sono probabilmente al di fuori dai limiti divulgativi del nostro Circolo. Ne esiste però una quarta, posteriore, dovuta a Irwin Shapiro che si ricollega strettamente alla deflessione della luce. Essa parla espressamente di ritardo nel tempo di arrivo di un segnale elettromagnetico che passi vicino al Sole. Anche di questo effetto abbiamo parlato, ma in modo molto semplificato, dato che il suo valore esatto abbisogna di una metrica adatta e di calcoli nuovamente non semplici.

In questo articolo vogliamo ritornarci sopra, diminuendo ancora la difficoltà di comprensione. Nel contempo, però, ci è sembrata cosa utile e mai ripetitiva quella di affrontare, sotto una diversa angolazione, la DIMOSTRAZIONE DELLA DEFLESSIONE DELLA LUCE. Vedremo che basta la teoria di Newton per comprenderla, anche se il valore finale, ricavato da Einstein, è decisamente maggiore di quello che avrebbe potuto calcolare Newton.

In poche parole, la vera domanda a cui vorremmo rispondere è la seguente: "Un segnale luminoso che giunge a noi passando vicino al Sole impiega più tempo del previsto  perché la luce rallenta?" Sembra una domanda veramente assurda, conoscendo un minimo di relatività generale, ma spesso viene fatta. Ed allora, oltre a darle una risposta, dilunghiamoci pure, nuovamente, sulla verifica della curvatura della traiettoria della luce facendo uso del solito, geniale, ascensore di Einstein in caduta libera. Utilizzeremo solo e soltanto il principio di equivalenza. Sono tutte cose già dette, ma vale sempre la pena battere su un chiodo su cui è appesa gran parte di tutta la fisica moderna.

La caduta libera... la base del fondamentale principio di equivalenza che ha permesso ad Einstein di iniziare e concludere il suo meraviglioso viaggio verso la relatività generale. Ricordiamolo almeno in parte: nessun esperimento fisico ci permette di dimostrare se siamo in caduta libera verso una massa (siamo in una campo gravitazionale) o se, invece, siamo nello spazio più vuoto possibile e lontani da qualsiasi massa. Parliamo proprio del celebre ascensore di Einstein (e anche del "suo" imbianchino, ovviamente...). Se stiamo cadendo dal centesimo piano perché qualcuno ha tagliato il cavo dell'ascensore, non ce ne accorgiamo assolutamente. Se abbiamo in mano una pallina e la lasciamo libera di cadere, essa non cade, dato che la stessa accelerazione verso il basso agisce sia su noi che su di lei, indipendentemente dalle masse, come mostra la Fig. 1, dove ascensore e due palline, una di lana e una di piombo, sono rappresentate nello spazio lontano da ogni massa e all'interno di un campo gravitazionale.

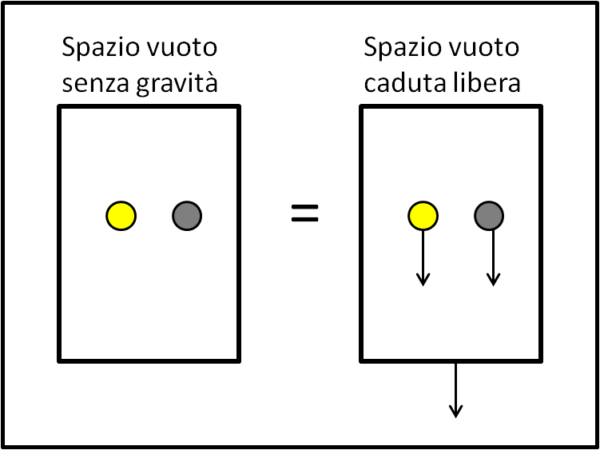
In poche parole, ciò che capita nell'ascensore che cade è del tutto uguale a ciò che capita in un ascensore  esente da qualsiasi accelerazione.

Questa conclusione che sembra banalissima (come tutte le grandi idee dei geni) ha fatto scattare la molla decisiva in Einstein, ma poteva benissimo essere già compresa da Galileo e da Newton. Soprattutto, li avrebbe portati a dimostrare che anche i fotoni, particelle senza massa, dovevano subire lo stesso processo, ossia venivano deviati all'interno di un campo gravitazionale.

Immaginiamo il nostro ascensore con un foro nella sua parte  sinistra, attraverso cui viene inviato un raggio di luce o, se preferite, un fotone. Immaginiamo anche che il nostro ascensore sia nello spazio vuoto, non soggetto ad alcuna gravità. Cosa succede al nostro fotone? Beh... fa ciò che DEVE fare il messaggero della luce: andare dritto percorrendo la minima distanza. In altre parole, uscire, dal foro posto esattamente nella parte destra, alla stessa altezza di quello di sinistra (Fig. 2).

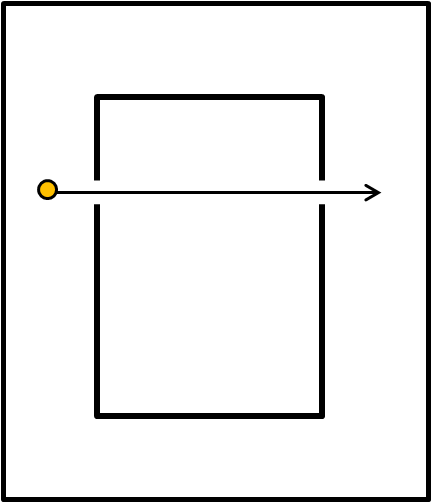
Questo è quello che vede chi sta dentro l'ascensore (e lo vede anche chi sta fuori se è anch'egli non soggetto ad alcuna forza o, ancora meglio, a nessuna accelerazione relativa all'ascensore, dato che appartengono allo stesso sistema di riferimento). Però, l'imbianchino ci ha dimostrato che chi sta cadendo in balia di un campo gravitazionale non se ne accorge e, quindi, deve percepire i fenomeni fisici nello stesso modo di quelli che avvengono nell'ascensore nel vuoto, lontano da ogni campo gravitazionale. La pallina che ha in mano deve stare ferma rispetto a lui e la luce deve attraversare l'ascensore in modo perfettamente rettilineo. Quest'ultima affermazione è fondamentale e la ribadiamo: nel vuoto assoluto la luce viaggia in linea retta (in fondo lo ha dimostrato anche Feynman nella sua QED...). Proviamo? perfetto, tutto torna, anche se la luce è talmente veloce che l'interno dell'ascensore potrebbe portarci a conclusioni sbagliate. Allarghiamo l'ascensore? No, meglio di no, almeno per ora, e accettiamo il principio di equivalenza. In poche parole, la stessa figura è quella relativa a ciò che vede e sente chi sta cadendo insieme all'ascensore in un campo gravitazionale

Adesso, però usciamo dall'ascensore che cade e guardiamo il tutto "da fermi", ossia secondo un altro sistema di riferimento. Bene,  ci rattristiamo immediatamente per l'imbianchino e capiamo che si illude di stare galleggiando nello spazio vuoto e che la sua pallina lo ha preso in giro... Rispetto al livello del suolo terrestre, dove sta l'osservatore, ossia Einstein, l'imbianchino si muove e come! E anche la pallina: entrambi cadono con la stessa velocità verso il basso e questa velocità aumenta costantemente, dato che ciò che rimane costante è solo l'accelerazione di gravità. Cosa succede, però, alla luce che è entrata nell'ascensore nello stesso istante in cui l'ascensore è stato lasciato libero di cadere? Beh... deve comportarsi nello stesso modo in cui si comportava nell'ascensore lontano da ogni campo gravitazionale. In altre parole, per chi sta dentro l'ascensore la luce deve andare dritta, ossia entrare da buco di sinistra e uscire dal buco di destra.

Su questo non ci sono dubbi, ce lo assicura il principio di equivalenza! Nel tempo, però, in cui la luce passa da un foro all'altro, chi sta fuori vede anche cadere tutto l'ascensore e anche il foro di uscita e quindi deve ammettere che il fotone non solo è andato verso destra, ma anche verso il basso, ossia ha descritto una linea curva, proprio come una palla di cannone sparata dalla cima di una montagna (Fig. 3). In conclusione, anche Newton avrebbe potuto concludere, se avesse avuto la tecnologia adatta, che la luce è costretta a curvare in presenza di un campo gravitazionale. Ancora una volta, tutto dipende dal sistema di riferimento da cui si osserva un fenomeno.

Notate bene come la pallina-fotone non cambi assolutamente la sua distanza dal pavimento dell'ascensore, ossia come essa vada perfettamente dritta durante la caduta. Chi è fuori invece la vede percorrere una curva parabolica. Deve, perciò, concludere che il fotone ha descritto una curva.

L'animazione precedente mostra molto bene sia la caduta dell'ascensore sia la traiettoria curvilinea della luce. Una volta capito il concetto, possiamo limitarci a  figure "ferme" e, disegnato l'ascensore solo nella posizione iniziale, mostrare sovrapposto a lui il percorso del fotone.  In tal modo si semplificano le figure, soprattutto in vista di ciò che andiamo a fare adesso.

Ci accorgiamo, infatti, che l'animazione precedente era enormemente esagerata, dato che nessun ascensore può cadere in ambiente "normale" -come nel nostro sistema solare, ad esempio- a velocità simili a quella della luce. Per ottenere ciò dovremmo andare proprio vicini a oggetti come i buchi neri.

Rimaniamo, perciò, nel nostro ambito planetario, dato che quando la teoria della RG è stata sviluppata le prove dovevano limitarsi a masse decisamente "risibili". Perfino la Fig. 4 ci mostra una deviazione della luce che è enormemente più grande di quanto potremmo mai ottenere con un ascensore, anche se fosse... gigantesco e cadesse verso il Sole.

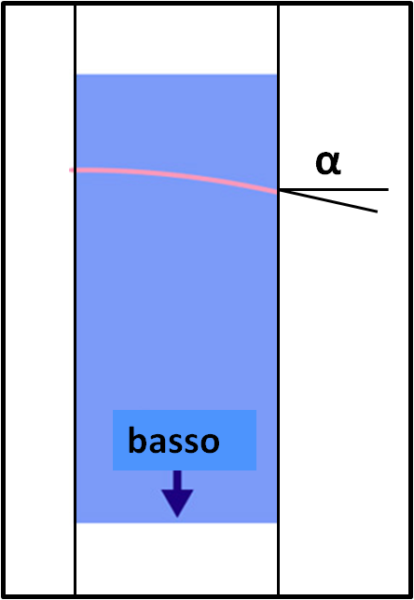
L'angolo tra la tangente alla traiettoria della luce uscente dall'ascensore azzurro e la linea orizzontale (pavimento dell'ascensore) lo chiamiamo α; esso ci indica di quanto è stata curvata la luce attraversando l'intero ascensore. Quest'angolo è  infinitesimo, dato che la larghezza dell'ascensore è molto piccola, Poco male... in fondo possiamo considerare tanti ascensori affiancati che cadono tutti assieme e seguire il tracciato della luce per un tempo e uno spazio assai più lunghi. Dividiamo perciò una certa regione di spazio in tante piccole strisce e in ognuna di esse inseriamo un ascensore, come mostra la Fig.5.

Sommando tutti i vari contributi  degli spostamenti infinitesimi dei vari ascensori, alla fine otterremmo uno spostamento misurabile (se visto da fuori). In particolare, potremmo misurare di quanto la luce è stata piegata a partire dal primo ipotetico ascensore rispetto all'ultimo. Essendo in uno spazio euclideo la faccenda sembra veramente banale. Sembrerebbe più che plausibile scegliere decisamente un ascensore molto più largo fin dall'inizio. Purtroppo (o per fortuna) lo spazio non è euclideo ma è curvo; in poche parole, NON possiamo accostare gli ipotetici ascensori.

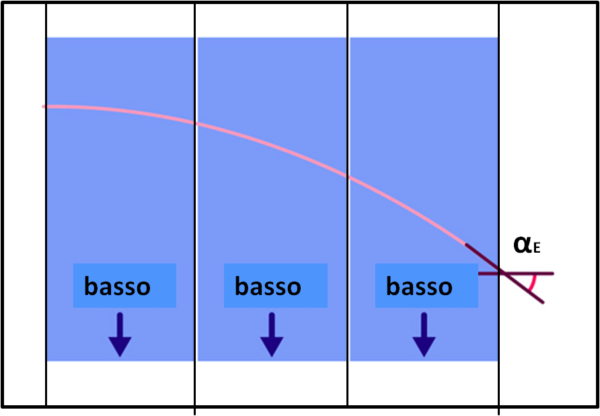
Per poterlo fare dovremmo usare ascensori deformati, più grandi verso il basso rispetto a quanto non lo siano verso l'alto. Sintetizzando in modo molto semplice, le strisce dei vari ascensori devono obbedire alla metrica che descrive lo spazio (in realtà, lo spaziotempo). Cosa succederebbe, in questo caso? Lo vediamo in Fig. 6.

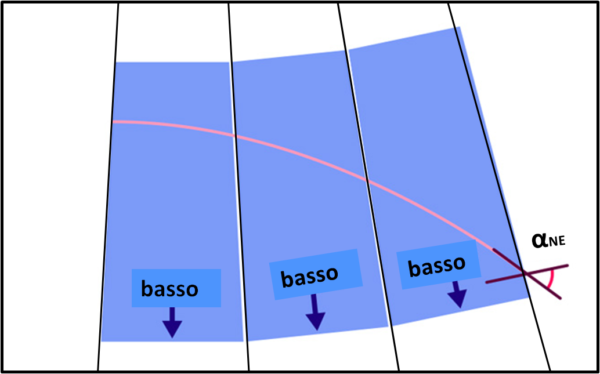
L'angolo formato dalla direzione del fotone che esce dall'ultimo ascensore è aumentato rispetto alla direzione del "basso" (il pavimento) dell'ultimo ascensore. Facendo i conti esatti con una metrica che soddisfi le equazioni di Einstein,  si ricava che la deviazione della luce è DOPPIA rispetto a quella che avrebbe potuto calcolare Newton (vedi anche QUI).

Resta tuttavia il fatto che sia in una caso che nell'altro la luce che attraversa un campo gravitazionale è costretta a curvare e questa curvatura diventa più grande se lo spazio non è euclideo. In altre parole, ancora, in entrambi i casi la luce è costretta a NON MUOVERSI IN LINEA RETTA,  ma compiere un tragitto curvo. Poco importa, in fondo, se questo percorso  sia quello reso obbligatorio all'interno di un uno spazio non euclideo.

Beh... la curvatura della luce la conosciamo molto bene ed è quella che causa  l'effetto lente. Tuttavia, una cosa è misurare la curvatura e un'altra é misurare il tempo che la luce impiega ad arrivare da una certa stella o galassia. Sarebbe stato lo stesso se non ci fosse stata la lente gravitazionale? Difficile rispondere se non conosciamo con esattezza la distanza della stella. Dobbiamo perciò limitarci al nostro Sistema Solare, dove le distanze tra i pianeti sono ben conosciute. L'oggetto migliore per causare una curvatura della luce è sicuramente il Sole, anche se la sua massa non è poi un granché per valutare certi effetti veramente microscopici a causa del suo campo gravitazionale. Se Eddington aveva potuto stabilire che la luce curvava, c'è voluto Shapiro, nel 1964, a determinare quanto tempo in più ci metteva.

Tanto per capire di cosa stiamo parlando, facciamo l'esempio di una pallina che vuole andare da Roma a New York. Il massimo che può fare è stare attaccata a terra e seguire un cerchio massimo.  Tuttavia, se potesse, la pallina preferirebbe entrare dentro la Terra e seguire il percorso rettilineo. Se non trovasse ostacoli o, in altre parole, se fosse stato scavato un tunnel rettilineo la pallina si comporterebbe come il neutrino ipotizzato da un nostro esperto ministro della Pubblica Istruzione qualche anno fa: via, dritti, senza ostacoli e senza dover curvare assolutamente alla faccia della sfericità della Terra! In fondo, in tal modo, potremmo accontentare i... "terrapiattisti"!

Cosa succede, allora, a un fotone che passa vicino a una stella o anche solo a un pianeta. Beh... lo sappiamo ormai molto bene: esso è costretto a percorrere una traiettoria curva, proprio come succedeva nell'ascensore. Questo ritardo è solo e soltanto dovuto al fatto che la luce, invece di andare in linea retta, è costretta a curvare, e quindi a fare un percorso più lungo. La velocità del fotone è sempre la stessa, ma se si allunga lo spazio da percorrere, ne segue, in modo elementare, che anche il tempo deve aumentare (è per questo che è stato possibile vedere due volte "in diretta" un'esplosione di supernova pochi anni fa). Abbiamo  un ritardo che avrebbe potuto confermare anche Newton, anche se con un valore decisamente minore, considerando uno spazio euclideo.

Grazie a Shapiro questo effetto di rallentamento è stato provato e oggi si è in grado di misurarlo molto bene. L'osservazione delle riflessioni radar da Mercurio e Venere appena prima e poco dopo essere eclissati dal Sole fornisce valori in pieno accordo con la teoria della relatività generale a un livello del 5%. Più recentemente, la sonda Cassini ha eseguito un esperimento simile che concorda con la relatività generale a un livello dello 0,002%