Questo articolo è inserito in "Storia dell'Unità Astronomica"

 

Gli anni passano e insieme a loro anche i secoli, ma la distanza del Sole non è più una problematica interessante. In fondo il Sole gira intorno alla Terra e la sua luce e il suo calore sono opera sicuramente divina. E’, probabilmente, un sacrilegio cercare di misurare qualcosa che è superiore alla limitatezza umana. Con l’avvento della teoria copernicana, però, tutto cambia e la scienza astronomica si scatena verso quello che viene, adesso, considerato un dato fondamentale.

E’, soprattutto, Keplero che mostra quanto questa misura sia una chiave straordinaria per aprire la porta dell’Universo, quello vero. Le sue tre leggi dicono molte cose, ma, in particolare, offrono la possibilità di calcolare le orbite dei pianeti.

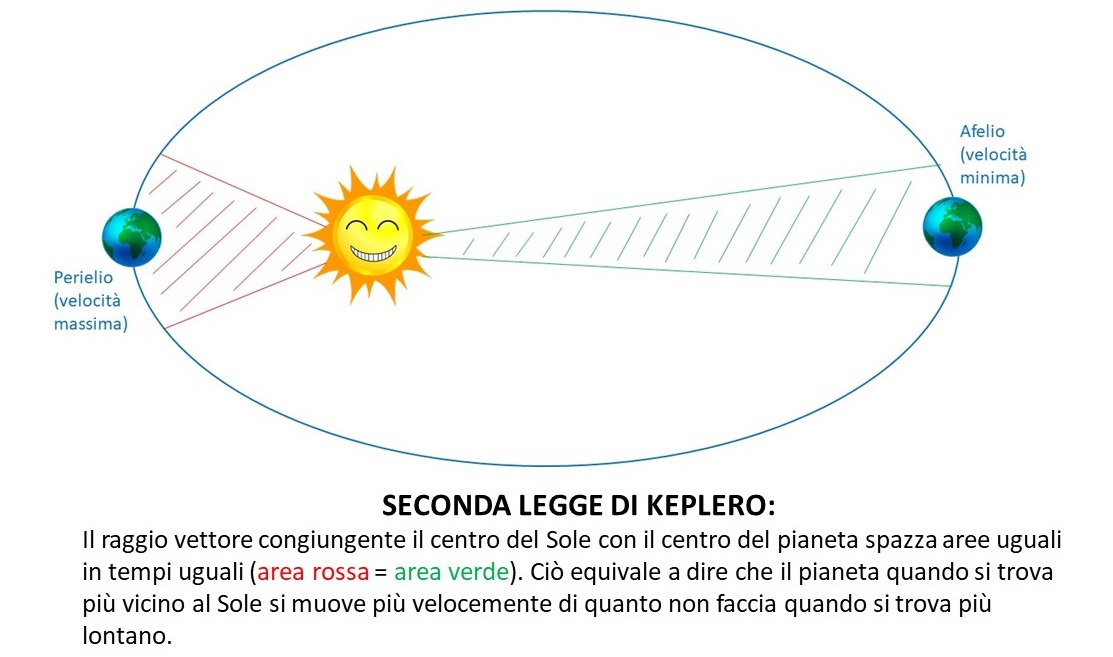
La terza legge è una vera manna per gli studiosi del tempo, dato che i periodi orbitali si possono ottenere con grande precisione attraverso quello sinodico.

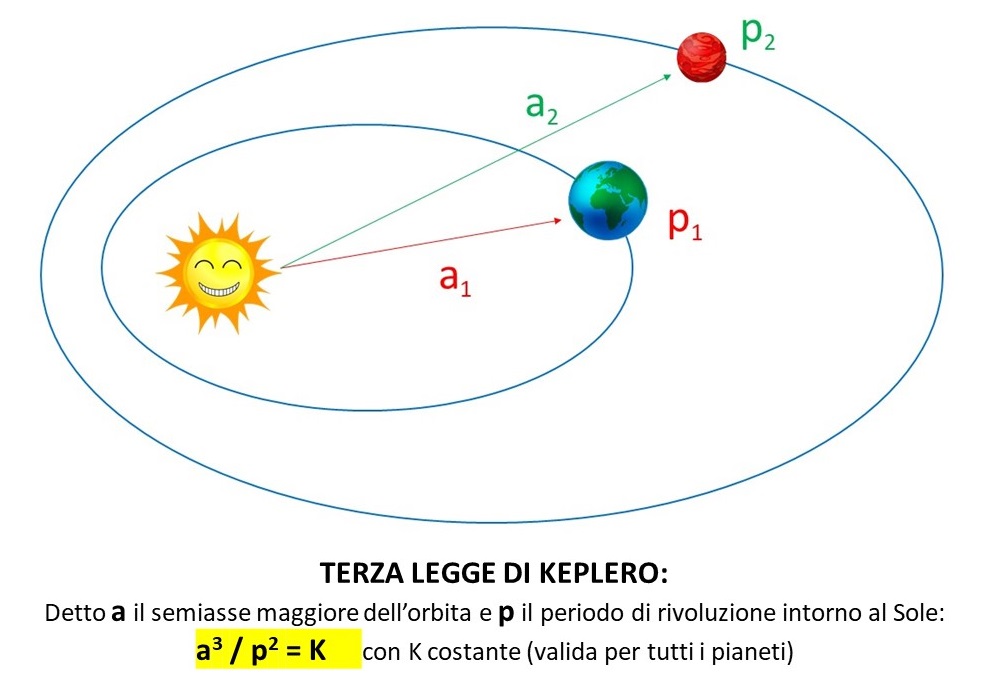
Tuttavia, manca ancora un dato fondamentale: il fattore di scala. Il Sistema Solare potrebbe essere grande o piccolo, dato che non si riesce a sciogliere il nodo dato dal rapporto tra il semiasse dei pianeti e quello della Terra. Si può dire quanto l’orbita di Giove sia più grande di quella terrestre, ma è ancora impossibile ottenere le distanze in chilometri o in miglia o in quello che si vuole. Le distanze vengono riferite solo a un semiasse di lunghezza sconosciuta.

Non solo, però…

La misura effettiva del semiasse dell’orbita terrestre può far volare verso le stelle e dare concretezza (forse) al sogno di Aristarco. Stiamo, ovviamente, parlando della parallasse annua, ormai quasi a portata di mano con l’avvento dei telescopi e di altre strumentazioni, ma, soprattutto, con la base della triangolazione a disposizione. Purtroppo, questa porta verso le stelle ha dovuto aspettare il 1838, quando Bessel riuscì a battere sul filo di lana Struve e Henderson.

Toniamo a Keplero e vediamo da vicino la storia della distanza del Sole o, in parole più “tecniche”, della parallasse solare. Cosa si intende per parallasse solare? L’angolo sotto cui il Sole vede il raggio terrestre. Oggi sappiamo che il suo valore è 8".794, ma quanta strada per arrivarci…

 

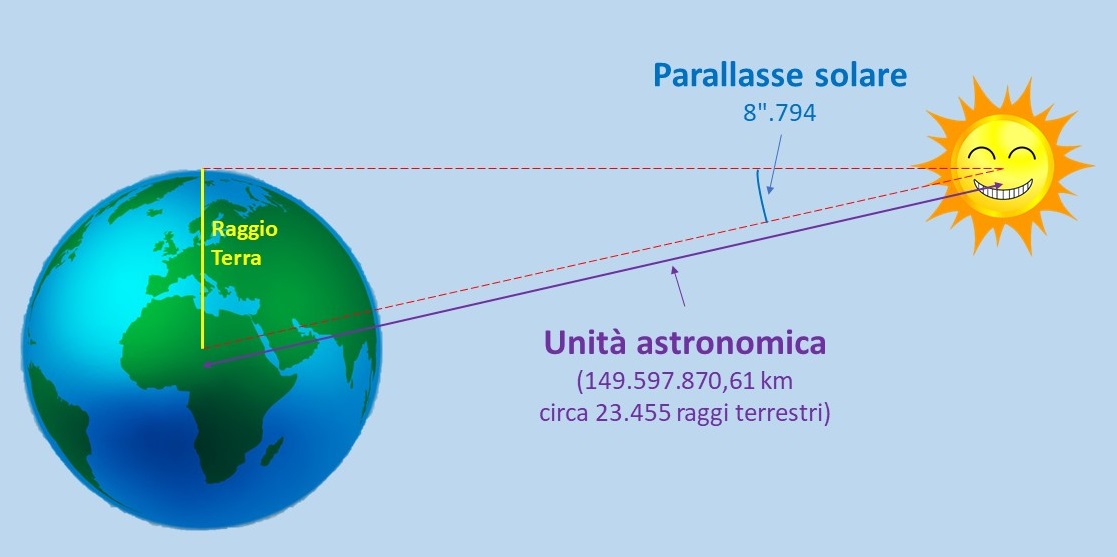
Il punto chiave era ovviamente trovare un metodo indiretto, dato che era decisamente impossibile recarsi sul Sole per osservare il diametro angolare della Terra o per misurare direttamente il diametro del Sole in chilometri!

Keplero, pur calcolando perfettamente l’orbita dei pianeti, in particolare Marte, non arrivò mai a una soluzione molto più accurata di quella di Aristarco. Egli si limitò a concludere che la parallasse solare doveva essere minore di 1’, ossia maggiore di 0.147 volte l’attuale Unità Astronomica. Ricordiamo che Aristarco ottenne il valore di 0.049, non credendoci, però, assolutamente, convinto che dovesse essere sicuramente maggiore (lo abbiamo raccontato QUI).

Vale, comunque, la pena vedere in modo grafico ed estremamente semplice come Keplero riuscì a calcolare l’orbita di Marte, grazie alle stupefacenti misure eseguite da Thyco Brahe.

Tracciamo, in Fig. 5, una circonferenza che rappresenti l’orbita terrestre. Immaginiamo di trovarci nella posizione T₁. E’ facile, anche a quei tempi, misurare la longitudine eliocentrica della Terra (rispetto al punto gamma). Sia essa L_1T. Osserviamo Marte e ricaviamo la sua longitudine geocentrica L_1M. Queste misure sono ampiamente spiegate nella descrizione dei sistemi di riferimento.

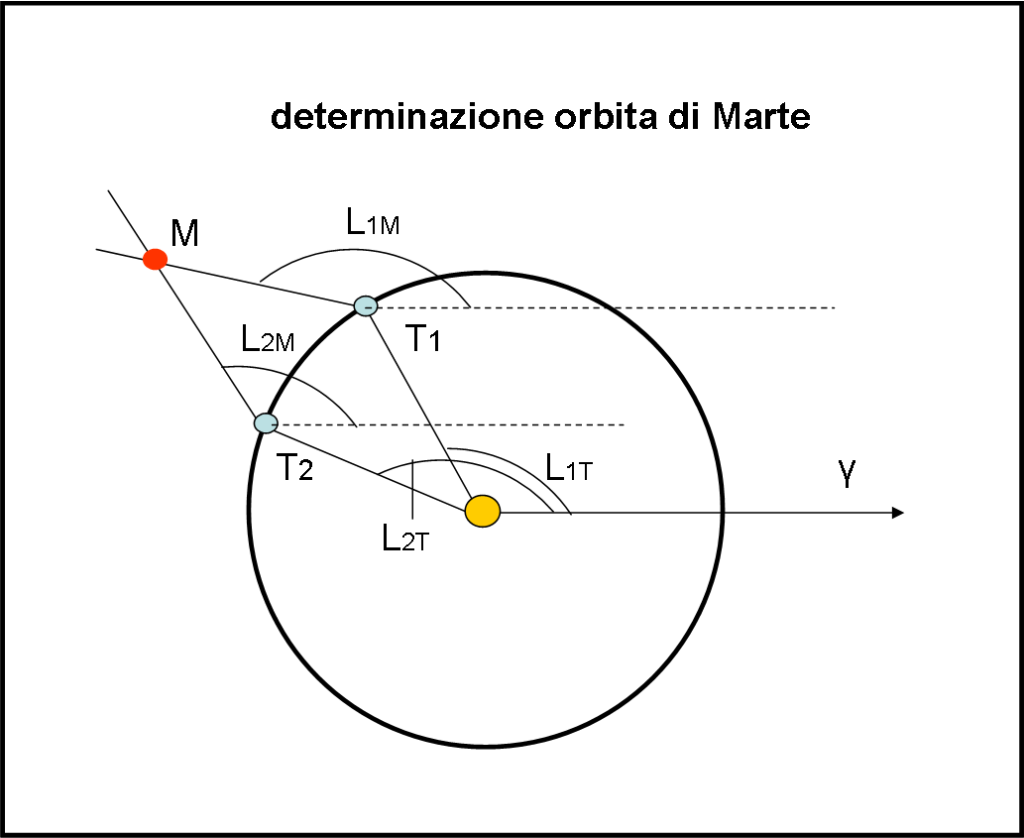
Lasciamo passare un periodo marziano (conosciuto molto bene). La Terra si troverà in punto diverso della sua orbita, ad esempio in T₂ con una longitudine eliocentrica L_2T. Osserviamo nuovamente Marte che ha ora una longitudine geocentrica L_2M. Tracciando le due linee che passano da T₁ e da T₂ e che hanno come angolo rispetto alla direzione del punto gamma le due longitudini marziane, queste devono incontrarsi nello stesso punto, dato che Marte ha compiuto esattamente un giro attorno al Sole.  Continuando in questo modo, si possono determinare graficamente molti punti dell’orbita marziana e ricostruire la sua traiettoria ellittica. Ovviamente, è poi possibile determinare tutti i parametri necessari per prevedere le posizioni future (QUI).

La terza legge di Keplero permette, comunque, di trovare, con grande precisione, il rapporto tra i semiassi delle orbite planetarie, dato che osservazioni e matematica possono risolvere il problema della traiettoria. Basta, infatti, conoscere i periodi di rivoluzione, facilmente ottenibili dai periodi sinodici.

P₁²/P₂² = a₁³/a₂³

E poi risalire alle posizioni lungo le orbite.

A questo punto vale la pena di riflettere sul contesto storico. Si è appena usciti da una visione dell’Universo puramente mistica e simbolica. Attraverso osservazioni, genio e tanta matematica, Keplero stila delle leggi che sono enormemente più avanti della conoscenza del cielo. Ricordiamoci che, a parte il Sole e la Luna, tutti i pianeti appaiono come stelle, dei punti irrisolvibili.

Solo il cannocchiale di Galileo permette di vederli, finalmente, come entità fisiche. Tuttavia, nella prima metà del '600 siamo veramente nella preistoria del Sistema Solare, per non parlare dell'Universo. Vi sono tre leggi fantastiche, ma i pianeti devono praticamente ancora nascere e niente si sa della loro distanza effettiva e delle loro dimensioni.

Non ci si deve, quindi, stupire che insieme a trattazioni matematiche estremamente elaborate ci siano ancora credenze mistiche o armoniche riguardo alle dimensioni dei pianeti e al loro posizionamento rispetto al Sole.

Keplero, ad esempio, era convinto che i volumi dei pianeti fossero proporzionali alle distanze dal Sole. Purtroppo, senza la conoscenza dei raggi effettivi o, quanto meno, di una legge che li governasse, era impensabile sfruttare le misure parallattiche dei pianeti, diventati veri dischetti con il telescopio, per determinarne la distanza. Solo conoscendo il raggio di un pianeta era possibile determinare, attraverso la misura angolare del disco, la distanza relativa alla Terra. Questa sarebbe stata la soluzione decisiva (Fig. 6): conoscendo il raggio R in chilometri e il suo valore angolare α, diventa un gioco per bambini “intelligenti” ricavare la distanza del pianeta dalla Terra (QUI un quiz papalliano che utilizza questa relazione)

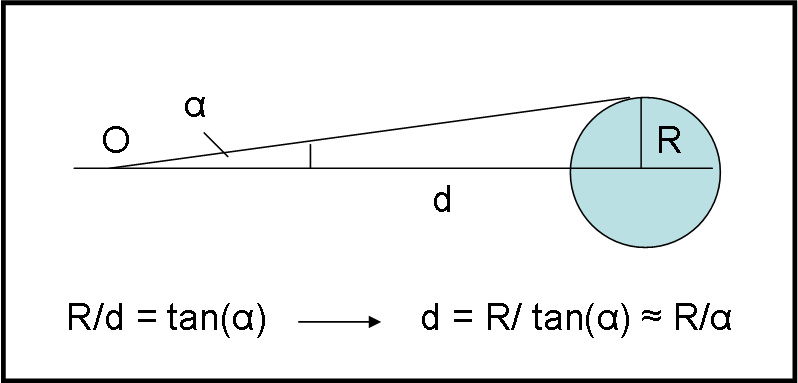
d = R/tan(α) ≈ R/α

A questo punto entrerebbe in campo Keplero con la sua terza legge. Conoscendo la distanza tra Terra e pianeta sarebbe possibile risalire in qualche modo alla distanza Terra-Sole, soprattutto se Sole e pianeta fossero perfettamente allineati (opposizione o congiunzione).

In pratica, la terza legge potrebbe essere scritta come segue, per un pianeta interno come Venere:

P_T²/P_P² = (a_T/a_P)³ = ((d_TP + a_P)/a_P)³ = (d_TP/a_P + 1)³       ..... (1)

Conoscendo i periodi, la distanza tra pianeta e Terra, l’unica incognita rimarrebbe il semiasse del pianeta: trovatolo, si troverebbero tutti gli altri, compreso quello della Terra. La formula è semplicissima nel caso di orbite circolari, ma la conoscenza delle altre leggi di Keplero permette anche di lavorare con orbite eccentriche, dato che una distanza variabile è “facilmente” riconducibile al semiasse attraverso gli angoli coinvolti.

Tutto bellissimo, ma restava il problema di fondo: niente diametro, niente distanza!

In qualche modo, era necessario fare delle assunzioni sul diametro dei pianeti, collegandoli a quello della Terra, ben conosciuto.

 

Un genio scomparso troppo in fretta

Ed ecco che riveste un interesse particolare la figura poco conosciuta di Jeremiah Horrocks. Di famiglia povera, non riuscì mai a terminare gli studi superiori, ma la sua analisi delle formule e dei dati a disposizione mise in luce un personaggio eccezionale. Purtroppo morì giovanissimo (22 anni), ma il suo contributo non passò inosservato tanto che lo stesso Newton lo giudicò come il “ponte” tra Keplero e la propria visione unitaria e globale.

Analizzando le tabelle allora in uso, Horrocks si accorse che vi era una discrepanza tra la posizione che Venere avrebbe assunto nel 1639 e quella ottenuta attraverso i suoi calcoli personali. Si parlava di un transito di Venere “mancato” di poco, mentre lui trovava invece un transito effettivo. Insieme a un amico, che si recò in una città diversa per sperare in uno sprazzo di sereno, attese l’ora X e possiamo immaginare la sua gioia quando tra una nuvola e l’altra il Sole si mostro finalmente con un dischetto circolare nero al suo interno (Fig. 7).

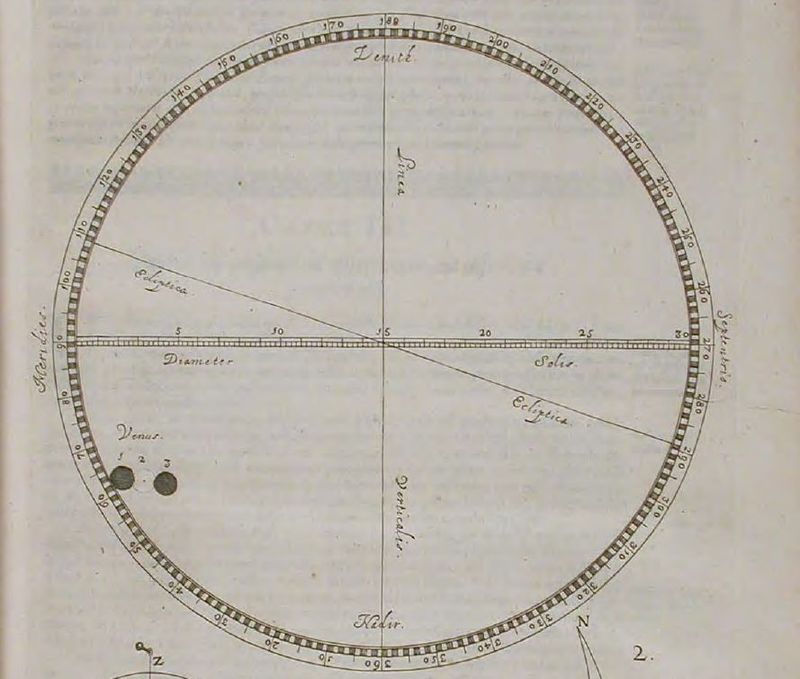
Non perse tempo ed effettuò le misure del caso buttandosi poi al lavoro. Era stato, probabilmente, il primo uomo ad assistere a un transito di Venere davanti al Sole. Oltretutto, in quell’occasione, nessun altro, tranne lui e l’amico, osservò il fenomeno, essendo basato sui dati di un quasi perfetto sconosciuto. E’ interessante notare come nel 1631 si ebbero a distanza di circa un mese sia un  transito di Mercurio che uno di Venere. Quello di Mercurio venne osservato dal più celebre Gassendi, a cui però sfuggì quello di Venere, dato che risultò non visibile da Parigi. Insomma, c’era molta meno frenesia dei giorni nostri… l’astronomia era dominio di poche menti eccelse.

Ma torniamo al nostro Horrocks. Lui costruì la Fig. 8, dove S è il Sole, M Mercurio,V Venere e T la Terra.

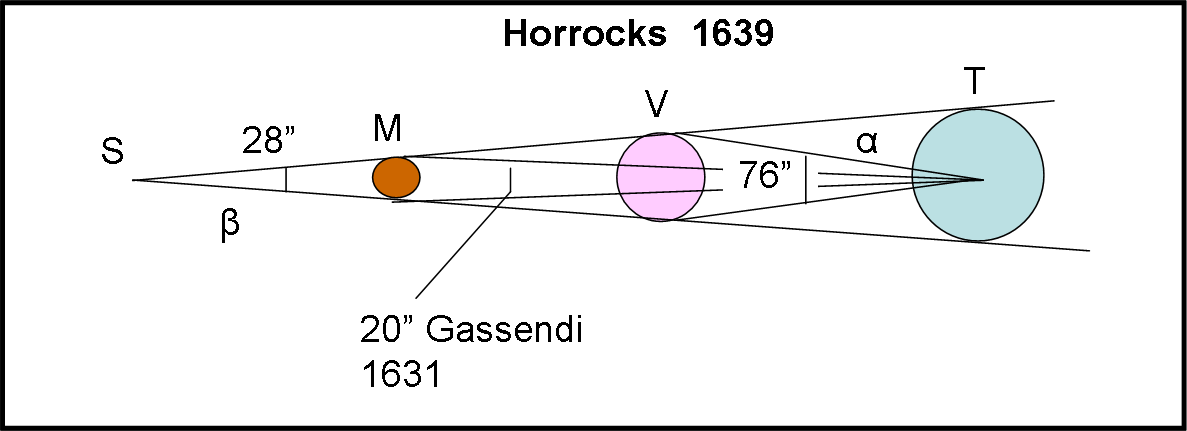
La misura del diametro angolare di Venere visto dalla Terra (osservabile molto bene essendo nero su sfondo chiaro) risultò essere uguale a 76”. Il raggio R_V di Venere poteva così essere ricondotto anche alla sua visione dal Sole. Infatti:

R_V = d_SVβ = d _TVα     …. (2)

d_SV è, ovviamente, il semiasse dell’orbita di Venere, mentre d_TV è la distanza Terra-Venere.

Ma, dalla terza legge di Keplero, come abbiamo visto precedentemente (1), è possibile ricavare il rapporto d_SV/d_TV, da cui la (2) permette di ricavare β, la parallasse di Venere, ossia l’angolo sotto cui il Sole vede Venere.

A questo punto, Horrocks era comunque in crisi, dato che il diametro di Venere (in chilometri) non poteva essere conosciuto. Non rimaneva che fare un’ipotesi sulle dimensioni dei pianeti, diversa da quella di Keplero. Secondo lui i raggi planetari dovevano crescere in modo proporzionale alla distanza dal Sole. In altre parole, TUTTI i pianeti, se visti dal Sole dovevano sottendere lo stesso angolo.  E aveva anche una prova a riguardo, proprio grazie a Gassendi e all’angolo che Mercurio aveva sotteso durante il suo transito, ossia 20”. Quest’angolo portava ad un angolo visto dal Sole abbastanza vicino a 28”. Quei 28” potevano essere proprio l’angolo costante. Non rimaneva che concludere che anche la Terra vista dal Sole doveva sottendere un angolo di 28”. In poche parole, la parallasse solare risultava essere uguale a 14”, ossia pari a un valore di 0.628 volte l’Unità Astronomica. Un bel salto in avanti rispetto ad Aristarco e a Keplero, ma ancora ben lontano dal valore corretto. Il Sole, comunque, e con lui tutti i pianeti, si allontanavano di molto dalla Terra…

Horrocks, sapeva unire una ferra volontà scientifica  a un senso umoristico e poetico, anomalo per il periodo storico e per un giovane di poco più di vent’anni. Da ricordare i suoi versetti sul secolo che si doveva aspettare per un altro transito di Venere:

I posteri testimonieranno il tuo ritorno

Gli anni dovranno srotolarsi,

Il magnifico spettacolo incontrerà, infine,

I nostri lontani occhi di bambino

 

Un genio molto fortunato

Maggiore fortuna e precisione si ottenne nel 1659 con Huygens. Tuttavia, il valore del suo risultato è decisamente basso e non venne considerato come indicativo. La spiegazione è semplice: Huygens aveva calcolato la parallasse del Sole attraverso una stima del tutto arbitraria. Sembra quasi impossibile che una mente come quella di Huygens, iniziatore del calcolo infinitesimale, ideatore della legge di conservazione dell’energia, enunciatore della natura ondulatoria della luce, costruttore dei più precisi orologi a pendolo, scopritore degli anelli di Saturno, studioso di ottica e delle sue applicazioni ai telescopi, e coinvolto in molte altre basi fondamentali della fisica moderna, potesse avere ancora visioni quasi infantili sui pianeti.

Come già detto, però, la matematica e la fisica avevano da molto cominciato il loro cammino moderno, mentre l’astronomia era nata da meno di mezzo secolo. La sua ipotesi era comunque armoniosa nella sua ingenuità: la Terra si trovava in mezzo a Venere e Marte e quindi doveva avere un raggio che stava a metà tra i loro due raggi.

Dopodiché agì in modo molto astuto… Lui conosceva con buona precisione (grazie anche agli oculari che aveva costruito…) il raggio angolare di Venere visto dalla Terra. Bastava porre il raggio effettivo di Venere uguale a quello della Terra e ricavare, dal solito triangolo “celestiale”, la distanza tra la Terra e Venere, in funzione del solo raggio terrestre. Tuttavia, dalle leggi di Keplero e conoscendo il momento dell’osservazione, poteva anche ricavare la distanza tra Terra e Venere in funzione della distanza Terra-Sole (la vera incognita). Come conseguenza poteva ricavare quest’ultima in funzione del raggio terrestre (noto).

A questo punto, ripeteva lo stesso procedimento per Marte e ricavava un nuovo valore della distanza Terra-Sole. Non gli restava che fare la media tra i due valori così ottenuti e avrebbe ottenuto un valore della distanza Terra-Sole relativo a un raggio terrestre che stesse  a metà tra quello di Venere e quello di Marte. Quasi inspiegabilmente (ma di certo fortunosamente) il valore finale era pari a 25.086 raggi terrestri, ossia 1,072 volte l’Unità Astronomica attuale. Un errore di solo il 7%, basandosi su una supposta armonia tra distanze dal Sole e diametri planetari…

Vi è da dire che la ricostruzione esatta del metodo usato da Huygens non è conosciuta (lui rimase molto nel vago), ma il valore finale sì, e anche l’ipotesi fondamentale di un raggio terrestre uguale alla media tra quello di Venere e Marte.

Altre fonti dicono che lui avesse misurato un diametro angolare di Venere pari a 1/84 volte quello del Sole, mentre quello di Marte fosse risultato 1/166. Ne seguiva che il diametro angolare di un pianeta di dimensioni intermedie doveva essere una via di mezzo, ossia:

(1/84 + 1/166)/2 = (0.0119 + 0.006)/2 = 1/111

Dato che il semidiametro del Sole visto da Terra era 0.253°, ne seguiva una parallasse solare pari a:

0.253/111 = 0.0023° = 8.2”

Valore che, riportato in unità astronomiche, risulta proprio uguale a 1,072.

L’ipotesi fatta ebbe scarsa considerazione presso i colleghi del tempo e la sua determinazione non venne assolutamente considerata un passo in avanti. Questo dovette aspettare il 1672, grazie a Cassini e al suo collega “viaggiatore” Richer.

Continua...

 

Gli articoli dedicati alla storia dell'Unità astronomica sono stati pubblicati nel 2017 (li trovate QUI), ma vi consigliamo di seguire la loro riedizione perché, oltre a riprodurre fedelmente quelli già usciti, contengono qualche informazione in più.