Questo articolo, oltre ad essere inserito nella pagina d'archivio "Velocità della luce", è una delle tante "ciliegine cosmiche" che potete gustare QUI

 

La velocità più difficile da misurare? La velocità della luce. Lo sapeva anche Einstein e ha dovuto imporre una "convenzione" per sviluppare la sua teoria. E le cose non sono ancora cambiate...

Tutta la relatività di Einstein si basa sulla costanza della velocità della luce. Ma, se c'è una velocità che non riusciamo realmente a conoscere è proprio lei! Lo stesso Einstein l'ha detto espressamente e ha deciso di accettare un valore "medio" non verificabile! Una "chicca" forse poco conosciuta, ma che sembrerebbe, comunque, non cambiare di una virgola la descrizione dell'Universo.

Come si fa a calcolare la velocità di un atleta impegnato nei 100 metri piani? Facilissimo. Si mettono due sensori, uno alla partenza e uno all'arrivo, i quali registrano il tempo esatto sia della partenza sia dell'arrivo. Dopodiché, conoscendo con grande precisione la distanza tra i due sensori, basta usare una formula veramente banale:

v = s/t

In parole immediate, si divide lo spazio percorso per il tempo impiegato a percorrerlo. Il risultato ci dà la  velocità cercata. In questo modo, possiamo dire di avere misurato una velocità (media) in una certa direzione. Ci stupiremmo non poco se si introducesse un nuovo tipo di gara, ossia quella in cui gli atleti, giunti all'arrivo, tornassero subito indietro fino alla linea di partenza. Chiamiamola 100 + 100. Nella seconda parte potrebbero impiegare più tempo, a causa, per esempio, del vento contrario. E questa differenza di condizioni al contorno potrebbe rallentarli tutti oppure, viste le caratteristiche fisiche, rallentarne maggiormente uno rispetto agli altri . Potrebbe capitare che due atleti arrivino al traguardo finale con lo stesso identico tempo. Come assegnare la vittoria in questa strana gara? Beh... potremmo dire che si è chiusa in parità e che entrambi hanno corso alla stessa velocità, pur sapendo che le velocità all'andata e al ritorno sono state completamente differenti.

Non credo proprio che una gara cosiffatta si svolgerà mai... Molto meglio misurare la velocità e dichiarare il vincitore lungo un solo tragitto, ossia lungo una sola direzione. Qualcuno potrebbe pensare che gli orologi alla partenza e quelli all'arrivo non siano perfettamente sincronizzati. Poco male... in fondo ci interessa solo il vincitore e la velocità finale potrebbe essere calcolata con un errore ridicolo, vista la distanza da percorrere e la tecnologia raggiunta oggi. Se proprio volessimo, potremmo cercare di sincronizzare ancora meglio gli orologi inviando un segnale luminoso tra uno e l'altro e vedere se esso arriva "quasi" istantaneamente. Il "quasi" dipende dalla velocità dell'informazione, ossia della luce, ma noi la conosciamo molto bene.

Concludendo, poco ci importa dell'errore che si può commettere nella perfetta sincronizzazione dei due orologi su cui agiscono i sensori. Questo errore è talmente piccolo rispetto al tempo impiegato che il risultato può essere considerato perfetto. Non vi è bisogno di fare i 100 + 100.

Le cose cambiano di molto, però, se la velocità che vogliamo misurare è proprio quella della luce, la stessa velocità a cui si muove l'informazione.

Possiamo usare lo stesso metodo per la velocità della luce? Purtroppo no, dato che la sincronizzazione di due orologi si può effettuare soltanto quando si è conosciuta la velocità della luce. Siamo, ovviamente, nel campo della relatività ristretta, in cui lo spostamento di un orologio o qualsiasi tentativo di sincronizzarlo con un altro DEVE fare uso dello stretto legame tra spazio e tempo. In altre parole, vorremmo misurare una certa velocità pur sapendo che l'errore introdotto si potrebbe conoscere solo conoscendo la velocità del nostro fotone o che dir si voglia. Un problema IRRISOLVIBILE.

Beh... in realtà, la velocità della luce è stata misurata in tanti modi e sempre in modo più preciso. Come? Senza assolutamente cercare di sincronizzare orologi, ma utilizzandone uno solo. Si invia il segnale fino a uno specchio e si aspetta che torni indietro. A questo punto basta scrivere:

c = 2s/2t

dove 2s è esattamente il doppio della distanza tra orologio e specchio (andata e ritorno) e 2t è il tempo totale impiegato tra partenza e arrivo. In poche parole si usa la strategia della gara 100 + 100, NON VALUTANDO ASSOLUTAMENTE L'IPOTESI CHE LA VELOCITA' ALL'ANDATA SIA DIVERSA DA QUELLA DI RITORNO.

Però, però... se all'andata fosse c1 e al ritorno c2, il calcoletto di prima mi porterebbe a scrivere:

c = (s/t1 + s/t2)/2 = (c1 + c2)/2

In parole molto semplici, utilizzando questo sistema di misura calcolerei un valore medio della velocità, ma non il valore lungo una certa direzione.

Eh no... non dovremmo certo accontentarci e avremmo veramente bisogno di una sincronizzazione perfetta tra orologi posti in luoghi diversi. Ma qui casca l'asino: per sincronizzare due o più orologi è necessario conoscere la velocità della luce in due differenti direzioni.

Consideriamo il caso classico utilizzato da Einstein. Mettiamo un orologio al centro e inviamo due segnali luminosi a un orologio O1 a sinistra e uno O2 a destra, ovviamente posti esattamente alla stessa distanza da quello centrale. Diciamo che gli orologi sono sincronizzati se li facciamo partire nello stesso momento. Ma siamo veramente sicuri che siano sincronizzati? Se la velocità della luce fosse diversa nelle due direzioni non lo sarebbero di certo. Per sapere qualcosa dovremmo farci rimandare indietro i segnali, ma le velocità si invertirebbero e torneremmo alla media di prima come mostra la Fig. 1.

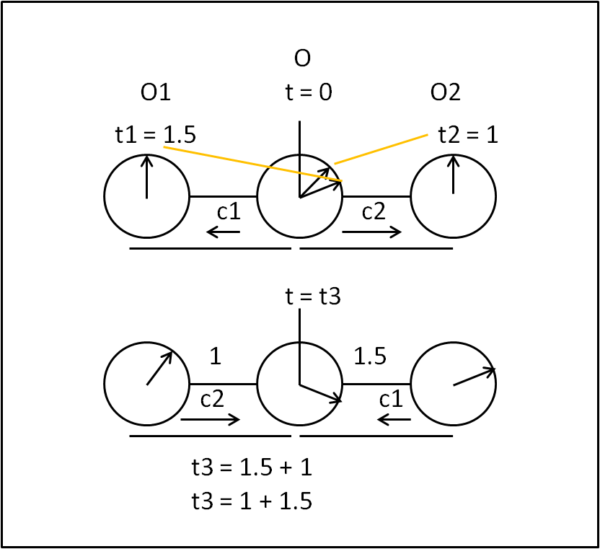
O manda il segnale, ma esso arriva prima in O2 che non in O1. Tuttavia, i due orologi partono in quel momento che non è lo stesso per entrambi. Il segnale di ritorno di O2, però, impiega più tempo per tornare in O. Ne consegue che i segnali tornano esattamente nello stesso istante in O, ma gli orologi in O1 e O2 non sono per niente sincronizzati!

Ne segue che l'unico modo per risolvere la faccenda è assumere un certo valore "convenzionale" per la velocità della luce, proprio come si evince dalla definizione di metro:

Fino al 2019: The metre is the length of the path travelled by light in vacuum during a time interval of 1/299792458 of a second (il metro è la lunghezza del percorso effettuato dalla luce nel vuoto in un intervallo di tempo pari a 1/2997922458 di secondo)

Dopo il 2019: Tutto resta invariato, tranne che considerare il secondo  in termini della frequenza Δν_Cs dell'atomo di cesio.

Misuriamo pure il secondo attraverso la frequenza del cesio, ma resta più che chiaro che viene imposta una certa velocità della luce, senza decimali. Una scelta che segue quanto affermato chiaramente da Einstein e già prima da Poincaré.

Riportiamo pari pari ciò che scrive Einstein nel suo "anno mirabilis" (1905), all'inizio del celebre articolo sulla elettrodinamica...

Ribadiamo, perciò, il punto chiave: "Cosa dire di tutti gli esperimenti che sono riusciti a determinare la velocità della luce con sempre maggiore precisione?". La risposta è molto semplice: "Tutti hanno sempre fatto la media tra velocità di andata e velocità di ritorno e poi, come detto nell'ultima frase di Einstein, hanno assunto come convenzione che la luce viaggi sempre alla stessa velocità in ogni direzione". In  parole più tecniche: hanno effettuato la misura con un solo orologio e uno specchio, accettando come dato di fatto che la luce abbia un comportamento perfettamente simmetrico. La simmetria è una norma molto seguita nell'Universo, ma non è sempre la regola, basti pensare alla proporzione tra materia e antimateria.

Per rendere il tutto molto semplice, utilizziamo il solito diagramma spaziotemporale di Fig. 2, con il tempo sull'asse verticale e lo spazio su quello orizzontale. Consideriamo anche due entità A e B che viaggino solo nel tempo, a una certa distanza fissa tra di loro, ossia siano reciprocamente fermi. B abbia uno specchio pronto a rimandare indietro il raggio di luce emesso all'istante t_o da A.

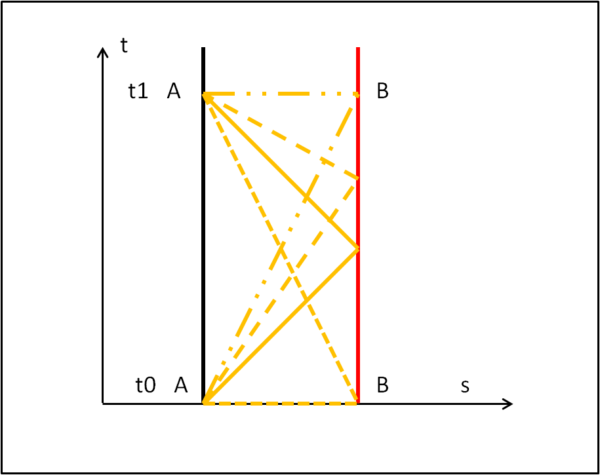
Bene se la velocità da A a B fosse uguale a quella del segnale di ritorno avremmo la ben nota figura in cui sia la linea AB che quella BA sono entrambe inclinate di 45° (avendo scelto una certa scala temporale e spaziale), linea arancione continua. A calcola il tempo Δt tra to e t1, conosce la distanza AB e può tranquillamente dire che c = (c + c)/2. Ma, cambierebbe qualcosa se c1 fosse più grande di c2 o viceversa? Assolutamente no, dato che anche in quel caso calcolerebbe per "convenzione" che c = (c1 + c2)/2. Una scelta "arbitraria" che però ci farebbe sorridere se ad andare da A a B fosse, ad esempio, una mosca. Ci accontenteremmo di dire che la sua velocità media è stata due volte la distanza diviso per il tempo di andata e riorno, ma non concluderemmo di certo che una mosca viaggia sempre alla stessa velocità in ogni direzione. Tutti i tragitti ABA darebbero sempre lo stesso risultato compreso quello limite per cui il viaggio da A a B (o da B ad A) fosse istantaneo e quello di ritorno (andata) fosse effettuato con c/2.

Qualcuno potrebbe dire: "Se fosse così, allora, l'Universo dovrebbe presentare caratteristiche assurde che non osserviamo assolutamente. Ad esempio, se la luce viaggiasse più veloce provenendo da destra  che non da sinistra, dovremmo vedere le galassie di destra molto più "vecchie" che non quelle di sinistra. Nel caso limite, quelle di destra potrebbero avere la nostra stessa età (velocità istantanea), mentre quelle di sinistra apparirebbero come erano nella loro infanzia (velocità pari alla metà del valore scelto per c). Una prova inconfutabile... ma ne siamo sicuri? Assolutamente no. Se la velocità della luce variasse con la direzione, anche la contrazione della lunghezza e la dilatazione del tempo muterebbero. Gli effetti della luce anisotropa su un semplice modello relativistico noto come l’universo di Milne ha dimostrato come l’anisotropia della luce causerebbe effetti di relatività anisotropa nella dilatazione del tempo e nell’espansione cosmica. Questi effetti annullerebbero gli aspetti osservabili di una velocità della luce variabile. In altre parole, anche se l’Universo fosse anisotropo a causa di una velocità della luce non costante, apparirebbe comunque isotropo.

Questo articolo riporta la dimostrazione analitica, ma a noi può bastare la conclusione:

" The anisotropic speed of light advocate must conclude that galaxies that are a given distance away have a faster recession speed in one direction than in the other, and the universe is expanding faster to the right or to the left. However, the dependence of redshift on the speed of light means that this does not change the appearance of the night sky. One side of the sky is not significantly more redshifted than the other. The initial velocities given to the galaxies at the beginning of the universe had just the right degree of anisotropy to balance the effect of anisotropic redshift. Perhaps at this point, the anisotropic speed of light advocate will suspect a fix, but there is nothing internally inconsistent or in contradiction with data about this model (L'ipotesi di una velocità della luce anisotropa porterebbe a concludere che le galassie poste a una certa distanza mostrerebbero una velocità di recessione diversa in una direzione piuttosto che in un'altra e, di conseguenza, l'Universo apparirebbe espandersi più velocemente a destra che non a sinistra (ad esempio). Tuttavia, il redshift è legato alla velocità della luce e ciò comporta una visione omogenea. Una parte dell'Universo non sarebbe significativamente più spostato verso il rosso rispetto all'altra. Le velocità iniziali assegnate alle galassie all'inizio dell'Universo avrebbero il giusto grado di anisotropia da bilanciare gli effetti dell'anisotropia del redshift. Forse, a questo punto, l'ipotesi dell'anisotropia della velocità della luce potrebbe apparire una stranezza gratuita, ma non vi è assolutamente niente di internamente inconsistente o in contraddizione con i dati per renderla inaccettabile)".

A qualcuno, forse, potrebbe tornare in mente l'etere... ma no, non ce n'è bisogno. Non rimane che sperare di trovare un metodo di misura veramente rivoluzionario che misuri la velocità unidirezionale della luce senza aver bisogno del suo valore. La relatività speciale, comunque, continua a funzionare perfettamente, tenendo sempre ben presente l'ammissione di base scritta chiaramente dallo stesso Einstein.

Le cose che sembrano le più ovvie sono, molto spesso, le più difficili da dimostrare.