Mi vedo costretto a riportare la soluzione di questo semplice problema, risolvibile con il solo ragionamento. Ragionamento che non è stato espresso nei due commenti di Agapito e Leandro, anche se il secondo ha dato almeno una regola, non spiegata, però, in modo veramente semplice.

Innanzitutto dobbiamo verificare se. senza provette inserite, il sistema sia in equilibrio. Sia 6 che 12 , per ovvia simmetria, confermano questo equilibrio.

A questo punto, il tutto si può riassumere nella somma che segue:

0  + 0 = 0

Intendiamo per 0 un perfetto equilibrio. La somma vuole dire soltanto che se si ottiene un equilibrio con un certo numero di provette e se si aggiungono altre provette, indipendentemente in equilibrio, l'equilibrio finale è conservato.

A questo punto, possiamo stabilire facilmente l'equilibrio con il minimo numero di provette pari e di provette dispari.

Sia per 6 che per 12 spazi vuoti il minimo numero di provette pari per ottenere l'equilibrio è ovviamente due, una situata esattamente in posizione opposta all'altra (i 180° di Leandro). Si ha l'equilibrio per un numero dispari di provette? Sicuramente sì e le provette devono essere almeno tre, tali da formare un triangolo equilatero. Ne segue che si può ottenere l'equilibrio in tutti i casi in cui sono ammesse una o più posizioni di equilibrio di due provette così come quello di tre o più provette, contemporaneamente, senza alcuna sovrapposizione di provette.

Vediamo prima il caso di 6.

Ovviamente una provetta non può mai dare l'equilibrio, che è invece raggiunto sempre da due provette messe in posizione opposta e anche da tre, sistemate in modo che formino un triangolo equilatero tra i loro centri.

Nessun problema, quindi, per due, tre, quattro (2 + 2 ) e sei (2 + 2 + 2).

Cosa succede invece per 5? Può essere raggiunta questa situazione con 2 + 3? Assolutamente no, dato che dopo aver inserito obbligatoriamente tre provette in equilibrio, le due che rimangono non possono essere mai poste in equilibrio (come dice Leandro l'angolo tra di loro sarebbe sempre minore di 180°). Vediamo la situazione in Fig. 1.

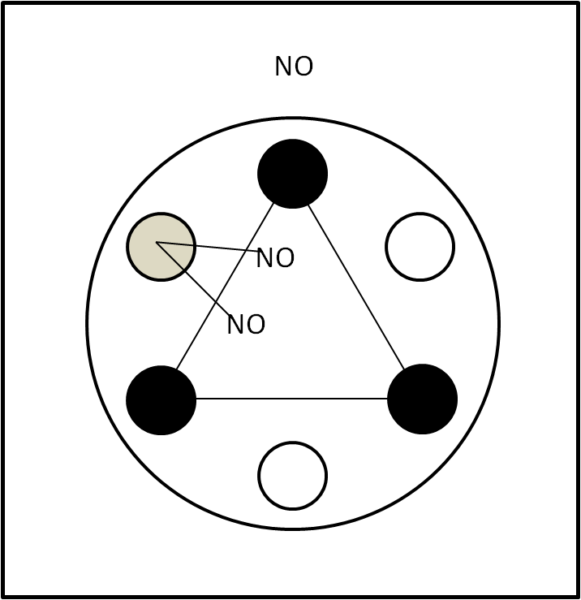
Passiamo al caso di 12 fori.

Si confermano ovviamente i numeri pari di provette che non hanno problemi, dato che basta continuare ad aggiungere due provette in posizione opposta ogni volta. Le cose migliorano anche per 5 provette dato che questa volta non hanno problemi di equilibrio (possono essere sistemate in modo che si sommino  3 e 2, avendo abbastanza spazi liberi in cui inserire le doppie provette). Il problema non sussiste nemmeno per sette provette, dato che vi è ancora spazio sufficiente per fare 3 + 2 + 2 (Fig. 3). Ovviamente nessun problema anche per 9  (3 + 3 +3), ma certo non per 11, dato che rimane un solo spazio vuoto.

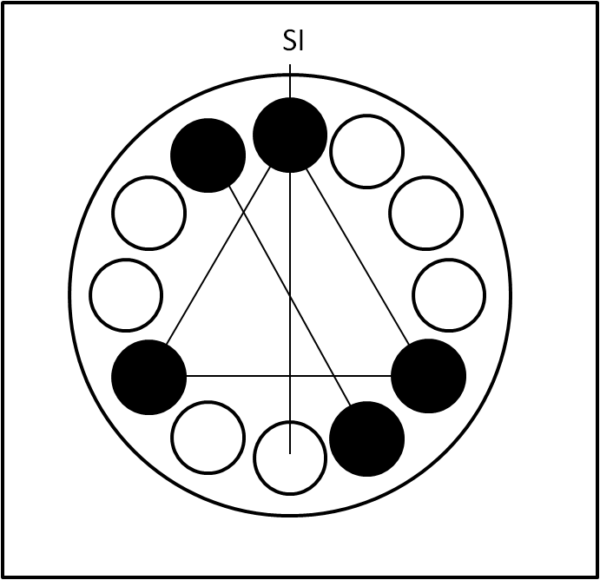
Lascio a voi il divertimento per un numero diversi di fori... ma posso, comunque, dire che la soluzione matematica del problema è estremamente semplice e  legata ai numeri primi, come si evince da quanto detto finora (basta tenere conto dei fori totali, di quelli occupati e di quelli che rimangono liberi):

Se n è il numero totale di fori e k sono i fori occupati dalle provette, è necessario che sia k che n - k siano numeri ottenibili dalla somma di fattori primi in cui può essere scomposto n (parole apparentemente complicate che non sono altro che la descrizione sintetica di quanto abbiamo fatto finora)... provare per credere:

Per n = 6  (3 x 2) e k= 5 (3 + 2), n - k = 1. Impossibile. Per n =12 (3 x 2 x 2)e k =5 (3 + 2), n - k = 7 (3 x 2 x 2) la regola funzione. Idem per k = 7 ( 2 + 2 + 3) che dà n - k = 5  (2 + 3)

N.B.: Ribadisco ancora che i nostri quiz non servono per vincere qualcosa, ma per insegnare anche ai meno esperti. Risposte "secche" senza spiegazione, servono, perciò, a ben poco. In altre parole, non si deve mostrare la propria bravura, ma aiutare chi non ce l'ha.