Categorie: Matematica
Tags: 15 anni Giappone quiz Sangaku tavolette dei templi
Scritto da: Vincenzo Zappalà
Commenti:12
Sommiamo i cerchi... ** (NEW)
Il problema è puramente geometrico, ma con la matematica si può trovare velocemente ed elegantemente una soluzione che così ovvia forse non è... Ricordiamoci l'estremo interesse dei giapponesi per questo tipi di problematica geometrica (le celebri TAVOLETTE Sangaku). Ho cambiato leggermente i dati di partenza per rendere più agevolo il calcolo.
Prendiamo una circonferenza di raggio unitario e inseriamo al suo interno dieci piccole circonferenze di raggio r in modo che formino la figura che segue. Chiamiamo n il numero di cerchi che appartengono alla riga orizzontale più lunga (nel nostro caso n = 4):
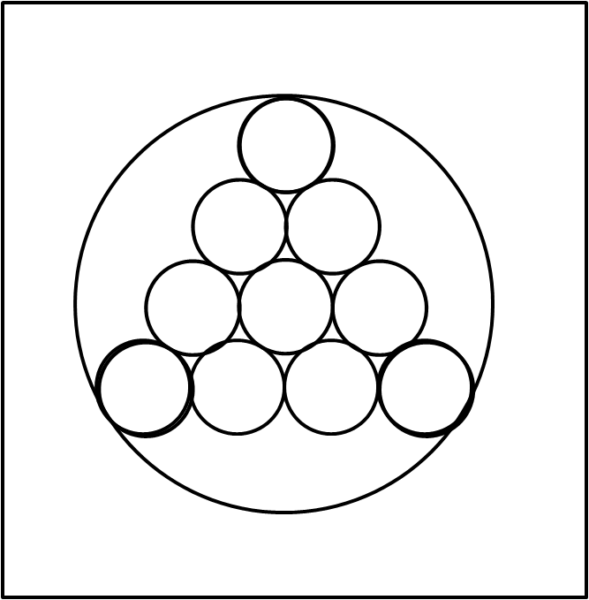
Ovviamente, possiamo variare il raggio r dei piccoli cerchi e di conseguenza il loro numero n.
Si chiede:
Qual è l'area minima della somma di tutti i cerchietti nel caso generale?
Mettiamoci nei panni dei ragazzi di 15 anni (di allora, però...).
QUI la soluzione






12 commenti
Non ce la faccio, ma posso permettermi di spiegare il mio ragionamento? Se no, Daniela ti prego di cancellare subito tutto.
I cerchietti sono n(n+1)/2. L'area di ciascuno è ovviamente πr2 e quindi ho l'area totale della quale devo trovare il minimo.
Ma c'è una relazione tra n e r? So che il lato del triangolo equilatero inscritto nel cerchione misura raggio (unitario) per radice quadrata di 3. Pensando a cerchietti infinitesimi potrei dire che r=2 volte radice di 3 fratto n.
Alla fine andando a sostituire trovo che A=(n+1) 6π...
Ma immagino che sono già completamente fuori strada :-(
caro Albertone,
cercare di spiegare il proprio ragionamento è sempre utile! Molto di più che dare un risultato corretto senza spiegazione. Prova a pensare a cosa succede se r va a zero... Ovviamente, la relazione tra n e r va trovata, ma non è complicata...
N.B.: Ho cambiato leggermente i dati di partenza per rendere più agevole il calcolo...
Ho scritto di getto con carta e penna il mio ragionamento, più bozza che definitivo...
#1 https://i.imgur.com/bAugxSw.jpg
#2 https://i.imgur.com/JFMTrTn.jpg
#3 https://i.imgur.com/Ffo3o8E.jpg
#4 https://i.imgur.com/yezfNyH.jpg
P. S. Ho usato la lettera c al posto della n
caro Andy,
aspetto a darti una risposta. Comunque, hai descritto il metodo in modo più che chiaro.
Io me l'ero immaginata più facile: una volta scritta la funzione dell'area (tutta nella variabile r) trovo il minimo con una derivata posta uguale a zero.
Ci provo oggi pomeriggio tra i tanti impegni pensionistici
Niente da fare. Ti prego di dirmi almeno se l'idea sarebbe giusta, magari lasciando perdere i calcoli.
Ho letto nei giorni scorsi che anche Newton calcolando un logaritmo a mano fino alla cinquantesima cifra decimale commise un piccolo errore aritmetico per cui la soluzione era giusta solo fino alla ventottesima cifra (in seguito si accorse dell'errore e lo corresse) [Il potere dell'infinito di Steven Strogatz].
caro Albertone, sei partito bene... ma poi hai ricavato n in funzione di r... prova a fare il contrario. Inoltre, lascia pure indicata la radice cubica di 3 e anche il pigreco ...
Pensavo che entrambe le strade fossero praticabili: o trovo il raggio o trovo il numero di cerchietti, questo o quello per me pari sono.
OK, ritento domani. Grazie per l'infinita pazienza date le mie infinitesime capacità
temo che tu abbia fatto un errore di calcolo... non di più...
come Newton?
più o meno...