Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Torniamo ai nostri amati greci antichi, soprattutto a quelli ingiustamente meno conosciuti, Ricordiamo, ad esempio, cosa avevamo scritto a proposito di Ippocrate di Chio:

Tra questi ve n'è uno non molto conosciuto ed è un peccato, dato che per primo riuscì a misurare esattamente l'area compresa tra due curve.

Oltra alle lunule, però, Ippocrate, usando la geometria attraverso il solo uso di riga non graduata e compasso, trovò un metodo semplicissimo per moltiplicare, tra loro, ogni coppia di numeri e, inoltre, fornì un metodo altrettanto semplice per calcolare la radice quadrata.

Partiamo dalla moltiplicazione (e, di conseguenza anche della divisione)...

Disegniamo due semirette qualsiasi (Fig. 1) che partano dallo stesso punto P e , attraverso il compasso, segniamo su entrambe delle tacche tutte uguali tra loro (questa è l'unità, del tutto arbitraria).

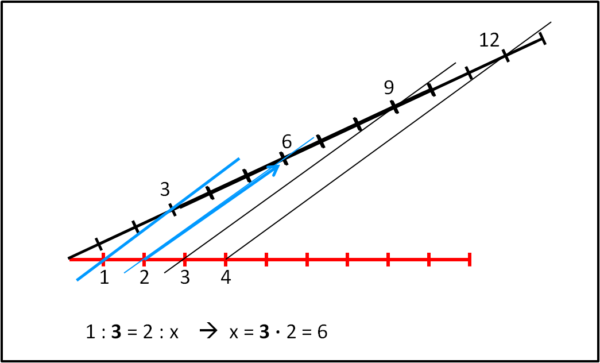
Vogliamo adesso moltiplicare, ad esempio, il numero 3 per il numero 2. Banale per Ippocrate... Uniamo tra di loro il punto 1 sulla retta orizzontale con il punto 3 sull'asse inclinato. Bene, basta tracciare la parallela a questa retta partendo dal numero 2 della retta orizzontale e vedere in che punto  questa retta interseca l'asse obliquo. Troviamo ovviamente il numero 6. Ovviamente, il procedimento si può fare al contrario e dividere 6 per 3, trovando 2. La dimostrazione ci riporta al teorema di Talete, rette parallele intersecate da due traversali, ma Ippocrate lo rende  simile a un vero calcolo matematico, cosa che dovrà, comunque, aspettare ancora tanti secoli per prendere il sopravvento sulla pura geometria.

Ancora più interessante e il "calcolo" geometrico della radice quadrata.

Tracciamo un segmento AH  di 4 unità e aggiungiamone una, ottenendo un segmento AB di lunghezza pari a 4 + 1 = 5. Tracciamo la circonferenza di diametro AB = 5, come mostra la Fig. 2.

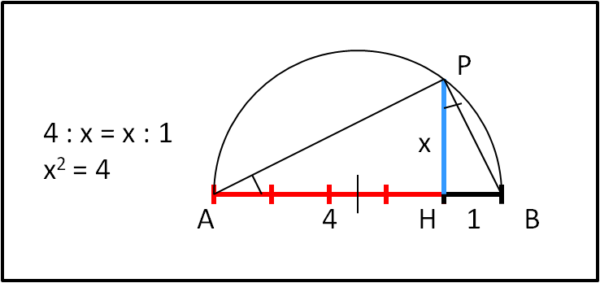
Dal punto H tracciamo la perpendicolare ad AB fino a incontrare la circonferenza in P. Ebbene, il segmento HP è la radice quadrata di AH. La dimostrazione è banale... Consideriamo il triangolo APB. Esso deve essere rettangolo in P, dato che è iscritto in una semicirconferenza di diametro AB (e questo lo sapeva già Talete). Tuttavia, per costruzione il triangolo PHB deve essere simile al triangolo AHP. Entrambi sono rettangoli, ma inoltre l'angolo PAB è uguale all'angolo HPB (complementari dello stesso angolo). Ne segue che i triangoli PHB e PHA sono simili. Si può, quindi, scrivere:

HB : HP = HP : AH

Da cui:

HP² = HB · AH

ma HB è uguale a 1, quindi

HP² = AH

Si dimostra perciò che HP è la radice quadrata del segmento AH. Notiamo che il metodo può essere applicato a qualsiasi numero anche non intero.

Una sciocchezza? non proprio, dato che si dovette aspettare fino a Cartesio per riprendere in mano la descrizione geniale di Ippocrate e applicarla al "calcolo" matematico che stava nascendo.