Per risolvere il QUIZ è bene definire almeno un paio di strategie operative. La prima è quella della divisione, che lascia il quadrato immutato e lavora soltanto con i rettangoli.

Cominciamo con 2 rettangoli e la soluzione è sicuramente la più ovvia, dato che basta dividere a metà il quadrato.

Il passo successivo è quello di dividere uno dei due rettangoli ottenuti in 4 parti (si divide per due sia il lato maggiore che quello minore e ognuno risponde ai requisiti del problema), In tale modo abbiamo il rettangolo del primo passaggio, rimasto tale e quale, più quattro nuovi rettangoli più piccoli, ossia 5 rettangoli in totale. A questo punto, basta prendere sempre il rettangolo più piccolo e dividerlo in quattro. Avremo 1 rettangolo grande, 3 medio e 4 piccoli, ossia 8 rettangoli. In poche parole, cominciando da 2 e aggiungendo 3 si ottiene il numero successivo ammesso e via dicendo...

2,  2+3 = 5,  5 + 3 = 8,  ecc.

La Fig. 1 mostra molto chiaramente ciò che abbiamo fatto.

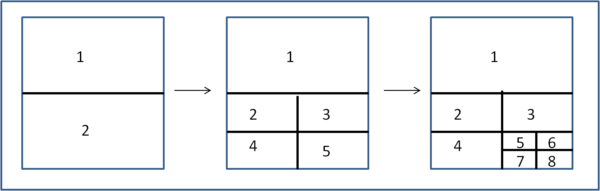
Riassumendo, se è ammessa una soluzione con n rettangoli è ammessa anche la soluzione con n + 3 rettangoli e via dicendo.

Per avere sotto controllo la situazione, scriviamo i primi numeri interi e mettiamo in grassetto quelli che danno un risultato conforme alle richieste del problema.

1  2  3  4  5  6  7  8  9  10  11 ...

Finora abbiamo lasciato immutato il quadrato di partenza, ma sappiamo che possiamo ingrandirlo a piacere con la sola condizione che rimanga un quadrato.

Allora riprendiamo il nostro quadrato diviso in due e aggiungiamo esternamente a lui dei rettangoli che abbiano come lato minore il lato del quadrato originario e come lato maggiore il doppio. Praticamente quello che mostra la Fig. 2

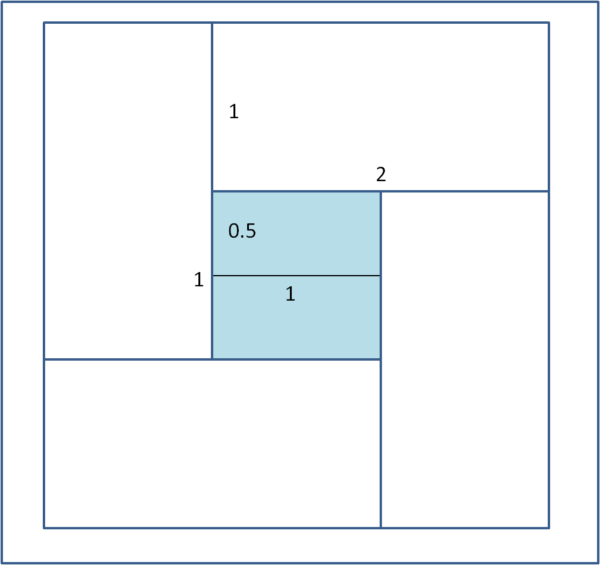
Il quadrato ha ora un lato doppio rispetto all'originario, ma esistono 2 + 4 rettangoli che possono coprirlo completamente.

In poche parole, vale la regola:

se n è un numero ammesso (ad esempio 2) lo è anche 2 + 4 = 6, e via dicendo. In altre parole, aggiungere 4 a ogni soluzione trovata porta a un risultato positivo

Riscriviamo i nostri numeri da 1 a 11, mettendo in grassetto anche quelli che rispondono al secondo criterio, ossia 2 + 4, 6 + 4 =10. Attenzione, però ... 5 è un risultato conforme e quindi, per il secondo criterio, lo deve essere anche 5 + 4 = 9. Ma non basta... 6 è un risultato conforme e quindi per il primo criterio deve anche esserlo 6 + 3 = 9.

1  2  3  4  5  6  7  8  9  10  11 ...

A questo punto, possiamo già dire una cosa fondamentale: 9, 10, 11 sono tutti ammessi e, allora, per il primo criterio, lo devono essere anche 9 + 3 = 12, 10 + 3 = 13, 11 + 3 = 14, ecc., ecc.

In poche parole TUTTI i  numeri interi che seguono quelli scritti devono per forza dare una soluzione conforme!

Vediamo cosa ci resta...

1   3   4   7

Beh... sicuramente l'1 non ha speranze, dato che si parte da un quadrato. Il 3 segue la stessa sorte così come il 4. Possiamo provare quanto vogliamo ma l'impresa è impossibile. Rimane il 7. Vi è qualche possibilità? Ebbene sì e la faccenda segue la procedura rappresentata in Fig. 3

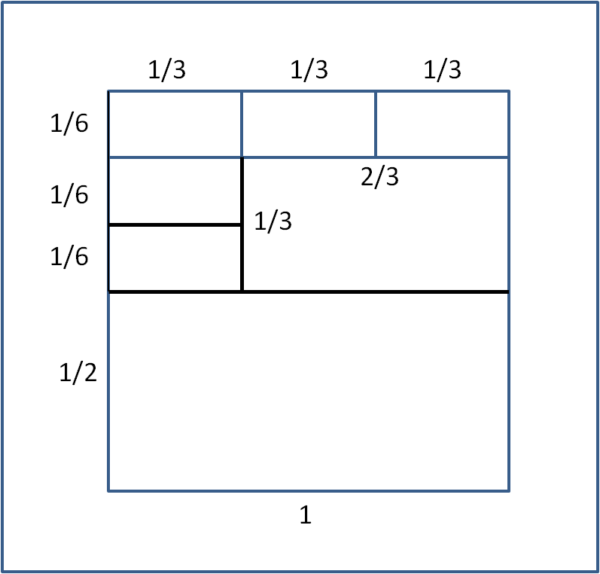
Fantastico anche se apparentemente inaspettato.

Insomma, come avevo preannunciato, è molto più semplice scrivere i numeri che non sono ammessi che quelli ammessi.

La soluzione è, quindi, che tutti i numeri danno la possibilità di usare i nostri rettangoli per riempire un quadrato, tranne che l'1, il 3 e il 4.

Grazie ai lettori che hanno partecipato al quiz e che un po' alla volta sono arrivati alla soluzione (Ernesto in particolare, con l'aiuto di Fabrizio)