Questo articolo fa parte della serie "Disegnare in tre dimensioni: tra storia e pratica"

Risolviamo il piccolo problema legato al pentagono e poi passiamo alla rappresentazione di un solido. Il Rinascimento si avvicina sempre di più...

Nell'articolo precedente abbiamo inserito un piccolo esercizio, ma probabilmente era fin troppo facile e nessuno ha proposto una soluzione. Comunque sia, preferiamo darla lo stesso per chiarire ancora meglio le semplici regole da seguire. In breve, la rappresentazione dall'alto della figura da rappresentare sul nostro disegno, è in grado di darci tutti i punti necessari per la rappresentazione finale sul piano di rappresentazione. Basta scegliere  la posizione dell'occhio e poi tracciare i segmenti che uniscono tutti i vertici del poligono con il punto O. In questo modo individuiamo perfettamente tutti i punti che corrispondono a questi segmenti sulla retta r.

L'unica cosa ancora da scegliere per eseguire il disegno prospettico è l'altezza dell'occhio rispetto al pt, ossia a r e individuare il fuoco F, ossia il punto all'infinito. Tutti questi facili concetti sono  già stati esaurientemente spiegati negli articoli precedenti.

Consideriamo allora, in Fig. 11, il nostro pentagono con la sua visione dall'alto, indicando tutti i punti che ci saranno utili (a sinistra). A destra invece consideriamo il piano del disegno, riportando sulla retta r i punti che abbiamo appena identificato. Ho disegnato la parte destra della figura aumentando le dimensioni di un fattore due per maggiore chiarezza.

Vi sono vari modi per eseguire il disegno, ma ne seguiamo uno che sembra il più semplice e intuitivo. Il pentagono può essere compreso in un quadrato rosso e di questo quadrato siamo più che capaci di darne la rappresentazione sul piano del disegno, conoscendo l'altezza h dell'occhio e quindi del fuoco verso cui dirigere tutte le rette parallele alle rette perpendicolari a r. I punti B e C si trovano immediatamente, alzando i punti L e N fino alle linee di fuga individuate da AF e DF. Otteniamo così la rappresentazione prospettica del quadrato rosso. Il lato AD sarà anche il lato del quadrato che abbiamo scelto stare sulla retta r. Il punto G, che deve stare sulla linea di fuga AD dà luogo alla intersezione K e quindi per identificarlo basta alzarlo fino a incontrare la linea di fuga AF. Tracciando da G una parallela a r , si identifica subito anche il punto I. Infine, vediamo che la retta MH è parallela ad AB e CD e quindi deve andare verso F. Tuttavia, il punto H deve anche stare sul lato BC. Basta identificare il punto d'incontro tra MF e BC per ottenere il quinto punto del pentagono e il gioco è fatto! Notate che il punto C appartenente al lato del pentagono che sta su r coincide casualmente con il segmento P, che sta sul segmento che proviene da I. Ne segue che I e P devono stare sulla stessa retta parallela a r, come si vede bene nella rappresentazione finale.

Con procedimenti analoghi e con una buona dose di fantasia si possono costruire figure oltremodo complesse. Basta solo non confondere i vari punti e procedere con molta cautela e con continui controlli.

In modo veramente simile a quanto appena fatto può essere costruito un cerchio. Oggi, con l'aiuto di un computer è possibile disegnare immediatamente un'ellisse che passa per tre punti, ma una volta si doveva avere più pazienza e aggiungere molti punti particolari per poi tracciare la curva a mano libera. Ma questo fatto non spaventava sicuramente i grandi geni del primo Rinascimento...

Per non farci mancare niente, disegniamo una circonferenza, sapendo già molto bene che la sua proiezione sul piano di rappresentazione diventa un ellisse, più o meno schiacciata a seconda dell'altezza di O e, quindi, di F.

Direi che non è più il caso di spiegare i vari passaggi  ed è più che sufficiente mostrare la visione dall'alto e la sua rappresentazione in Fig. 12

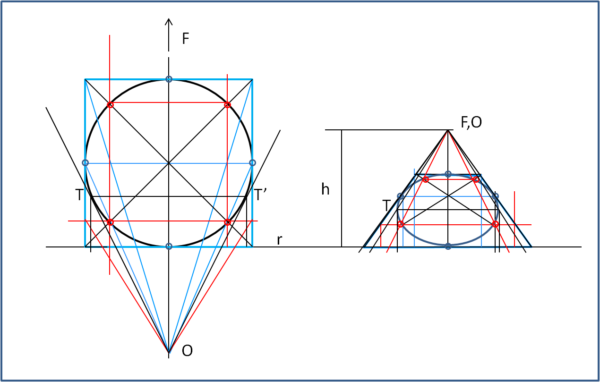
Notiamo che i punti più lontani dalla linea mediana (OF) corrispondono ai punti di tangenza del cerchio visto da O. Ne segue che questi due punti, T e T', individuano l'asse maggiore dell'ellisse apparente.

Beh... direi che siamo pronti a disegnare una figura solida che abbia una certa altezza k. La faccenda diventa molto semplice, dato che l'altezza c sul piano di rappresentazione si deve mantenere. Consideriamo, allora, un parallelepipedo, come in Fig.... Sappiamo disegnare molto bene la sua base sul piano terra di lati a e b. Ma sappiamo molto bene anche tracciare la sua altezza c sul piano di rappresentazione (è un dato del problema). Risulta anche ovvio che i lati b del parallelepipedo posti all'altezza c devono anch'essi andare verso il fuoco F. Basta allora alzare i punti B e C fino a incontrare le linee di fuga della faccia superiore. Banale, veramente banale.

Non ci resta (per il momento) che disegnare un solido "vuoto", ossia, in poche parole, una stanza o, in generale, uno spazio in cui inserire tutti solidi "pieni" che vogliamo. Notiamo che quando parliamo di solidi pieni, come ad esempio un parallelepipedo, parliamo anche di figure umane le quali sono facilmente contenute nel solido in questione. Ottenuto questo possiamo poi passare alla versione pratica della visione prospettica attraverso alcune opere fondamentali dei Maestri del quattrocento.

La Fig. 13  illustra una stanza con i suoi lati che la delimitano.

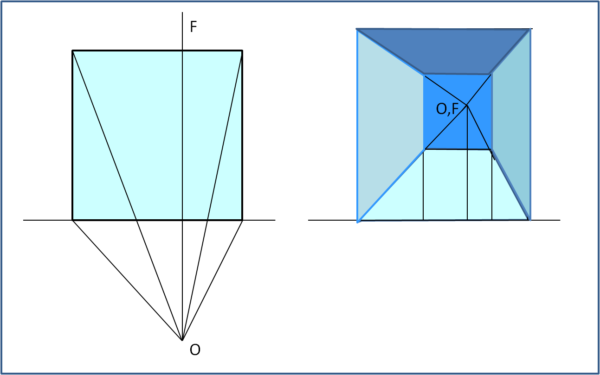
Praticamente è come disegnare un solido, ma i cui lati non sono altro che le pareti del solido vuoto viste prospetticamente dall'interno. Abbiamo usato colori diversi per mettere meglio in evidenza la visione finale, costruibile esattamente con le regole che ci hanno permesso di disegnare un solido pieno.

La Fig. 14 mostra come sia facile inserire un volume pieno all'interno di una stanza vuota.

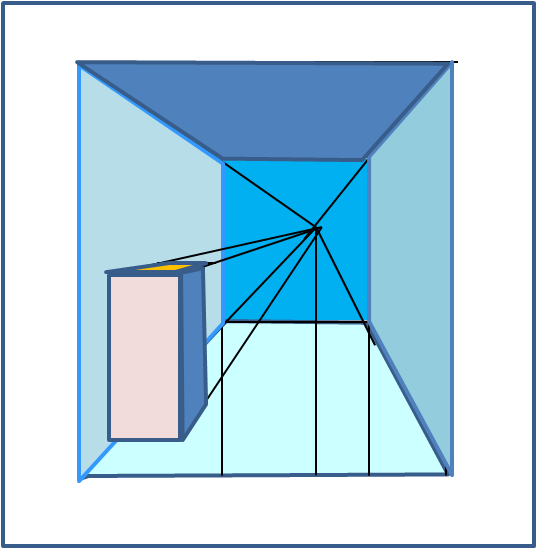
A questo punto abbandoniamo per un po' le rappresentazioni geometriche ed entriamo di prepotenza nella storia dell'arte. Anno apparentemente fondamentale è l'anno 1413 e vedremo perché.

continua...