La serie di articoli dedicati ai cerchi di Archimede è inserita nella pagina d'archivio Antichi Greci, che passione!

 

Dopo il coltello del calzolaio, Archimede introduce, nel lemma 14, anche la saliera (Salinon). il nome deriva sicuramente dalla forma, anche se vi sono altre ipotesi in proposito.

In Fig. 17, sia AB il diametro di un cerchio. Su di lui indichiamo due punti, D ed E, tali che AD = EB. Tracciamo il semicerchio di diametro AB rivolto verso l'alto (C). Con diametro AD ed EB tracciamo due semicerchi dalla parte di C. Infine, con diametro DE tracciamo un semicerchio dalla parte opposta (F). Otteniamo la figura colorata in grigio che prende il nome di Salinon. L'area di tale figura curvilinea è uguale a quella del cerchio di diametro CF.

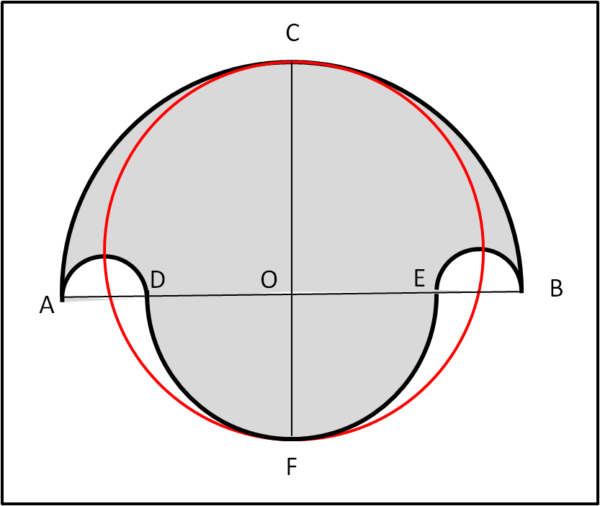
Dimostrazione:

Basta assumere come vere due relazioni (già provate da Euclide):

AE² + AD² = 2(AO² + OE²)

e

CF = EA

Ricaviamo la prima abbastanza facilmente:

AE² + AD² = (AO + EO)² + (AO - DO)² = (AO + EO)² + (AO - OE)²

AE² + AD² = AO² + EO² + 2AO EO + AO² + EO² - 2AO EO

AE² + AD² = 2(AO² + OE²)

mentre la seconda è immediata:

CF = OC + OF = OA + OE = EA

Possiamo calcolare l'area della "saliera" togliendo i semicerchi piccoli dal semicerchio di diametro AB e aggiungendo il semicerchio di diametro DE. Prima, però, traffichiamo un po' con la somma AB² + DE², che ci interessa, dato che è proprio somma dei due semicerchi di diametro  AB e DE, a parte un fattore π/2, utilizzando quanto già dimostrato ...

AB² + DE² = (AE + EB)² + (AE - AD)² = (AE + AD)² + (AE - AD)² = 2(AE² + AD²)

AB² + DE² = 4(AO² + OE²) =  2(AO² + OE²) + 2(AO² + OE²)

AB² + DE² = 2((AO² + OE²) + (AO² + OE²)) = 2((AO² + OE² + 2AO OE) + (AO² + OE² - 2AO OE))

Abbiamo aggiunto e tolto una stessa quantità

AB² + DE² = 2((AO + OE)² + (AO - OE)²) = 2EA² + 2AD² = 2(CF² + AD²)

AB² + DE² = 2(CF² + AD²)

evitando sempre di introdurre π/2 , il tutto equivale a scrivere una relazione tra le aree SC dei semicerchi e del cerchio C che ne derivano

SC_AB + SC_DE = C_CF + 2SC_AD = C_CF + SC_AD + SC_AD = C_CF + SC_AD + SC_EB

SC_AB + SC_DE  - SC_AD - SC_EB  = C_CF

Il che vuole proprio dire:

area Salinon = area cerchio di diametro CF

Da quanto detto, non è certo difficile enunciare un'altra proprietà del Salinon, ossia che il suo perimetro è pari alla circonferenza di diametro AB, infatti (evitando di scrivere 2π):

AD + DE/2 + AB/2 = 1/2(2DA + DE + AB) = 1/2(AB + AB) = AB

perimetro Salinon = circonferenza di diametro AB

Si attribuiscono ad Archimede o alla sua scuola altre figure basate su cerchi che ricordano attrezzi di uso comune, come la "scure" (pelecoide), la falce (depranoide) e il fuso circolare. Ne parleremo la prossima volta.

 

continua...