Due su parecchi milioni *****
Questo quiz è sicuramente tra i più difficili che siano mai stati proposti, pur basandosi soltanto su una ... somma. Io mi sento di dargli anche 5 asterischi, ma con voi non si sa mai...
Il problema consiste nel riuscire a scrivere il numero più vicino possibile a 82, attraverso un certo numero di ADDIZIONI consecutive.
Per fare quanto richiesto è necessario operare con la seguente serie di cifre e punti:
∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 ∙ 9 ∙ 0 ∙
Ogni numero (sette in tutto) può essere usato una e una sola volta nelle somme che possono essere in numero qualsiasi. Ad esempio si può scrivere 57 + 48, ma non 54 + 48.
I punti (otto in totale) possono essere utilizzati in due modi:
(1) Come inizio di un decimale. Ad esempio: .46, senza bisogno di inserire lo zero prima del punto.
(2) Come indicazione della periodicità di un certo numero. Ad esempio: significa .565656... con 56 periodico, mentre
significa 0.34444444... con 4 periodico e
significa 0.7777777... con 7 periodico
Sia le cifre da 4 a 0 (4 5 6 7 8 9 0) che gli otto punti devono essere utilizzati tutti almeno una volta, ma non di più o di meno.
Vincerà il nostro premio di ... "niente", chi riuscirà ad avvicinarsi di più al risultato di 82.
Forza miei prodi... le vacanze sono quasi finite!
QUI la soluzione
16 commenti
Una possibile soluzione
75+6+.98+.04 = 82,02
Gulp non avevo letto bene, che devono essere usati anche tutti gli otto punti.
Come non detto
Oltre alla soluzione che ho scritto sopra,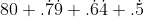
, ce ne sono anche altre dello stesso tipo nelle quali cambiano i due numeri periodici centrali. La condizione è che la somma dei due numeri interi ottenuti prendendo le cifre dei due numeri periodici dia 143. Ad esempio, nel soluzione sopra abbiamo 79+64=143. Con 7, 9, 6 e 4 si possono ottenere altre combinazioni che fanno 143.
Il numero 143 non è un numero magico, è ottenibile con alcuni passaggi matematici.
Caro Fabry,
il succo di tutto è che, prendendo 80 come ovvio numero da considerare intero, la somma delle parti periodiche rimanenti dia luogo a 198... dato che 99 deve essere al denominatore. Quello che potrebbe ingannare è il 5 periodico che, però, coincide co 55 periodico. Forse qui sta la parte meno intuitiva... Non penso, invece, che si possa prendere un numero intero diverso da 80.
Comunque sia, lasciami ribadire che sei stato bravissimo (te lo posso assicurare!). Vediamo se qualcun altro ci arriva...
Questo quiz credo dimostri che certe volte la difficoltà di un problema è soggettiva o magari dipende dalla fortuna di imboccare presto la via giusta. Nel mio caso è stato risolutivo capire, dopo qualche incertezza, che l'intero probabilmente doveva essere 80 e che il più vicino possibile era proprio il più vicino possibile. Il resto è stato in buona parte un percorso definito dai vincoli del problema, in particolare l'uso dei punti, e da qualche sbiadito ricordo delle scuole medie. Anche il passaggio tra 5 e 55 è venuto direttamente dall'algebra. Francamente ho impiegato di più a capire "Il club privato".
Comunque, caro Fabry... il quiz faceva parte di un di concorso con mille dollari di premio (a fine secolo XIX) che ha visto coinvolto un numero enorme di persone (milioni) e solo due hanno dato la risposta giusta! Ribadisco la tua bravura senza tema di smentita!
Caro Enzo ci riprovo.
Dunque, innanzitutto il numero intero può essere solo 80.
Per esempio se si usasse 79, comunque gli altri numeri non sarebbero sufficienti per raggiungere il traguardo di 82 (esempio .8888888888 + .666666666 + .5555555555 +.4 0404040404040 = 2,515151, ma ne servirebbero 3).
A questo punto usando come numero intero 80, rimangono i numeri 4;5;6 e8 e ben 8 punti per raggiungere il traguardo di 82.
La sequenza che più si avvina a 2 (numero mancante per arrivare a 82) è questa:
.79 (con 79 periodico, quindi uso in totale 3 punti di cui 2 sopra il 79);
.64 (con 64 periodico, quindi uso in totale 3 punti di cui 2 sopra il 64);
.5 (con 5 periodico, quindi uso in totale 2 punti di cui 1 sopra il 5).
Ne segue che:
80 + .797979797979797797979 + .6464646464646464 + .55555555555555555 = 81,99999
Chiedo scusa per le imprecisioni e i refusi.
:oops:si vede che stanotte ho dormito poco e faccio pasticci.
Aggiustiamo le cose, se poi si può meglio cancellare il commento precedente.
Dunque in realtà dopo aver scelto 80 come numero intero rimangono i numeri: 4; 5; 6; 7; 9.
Inoltre per poteri usare 8 punti servono almeno 5 numeri sui 7 totali, anche per questo si può usare solo 80 come numero intero.
Davvero, davvero, una figuraccia dietro l'altra
Anch'io parto dal presupposto che, dati i numeri e l’obiettivo (82),
partendo dall’intero più prossimo a 82 che è 80, il percorso risolutorio potrebbe essere quello giusto.
Eliminando dalla sequenza i numeri 8 e 0 (che formano 80) i rimanenti combinati tra loro secondo le regole, devono avvicinarsi il più possibile a 2 o anche raggiungerlo.
I numeri disponibili sono allora: 9, 7, 6, 5, 4.
I puntini che indicano la periodicità sono 8; se considero solo una cifra tra quelle disponibili per costruire il numero periodico, utilizzo 2 puntini e quindi ne rimangono 6 disponibili, che posso distribuire tra gruppi di cifre rimaste prese a due a due.
Allora, con il vincolo della periodicità, imposto un’equazione del tipo:
cifra singola / 9 + (cifra doppia 1 + cifra doppia 2) / 99 = 2
con la simbologia adottata nel quiz:
.cifra singola· + .cifra doppia 1·· + .cifra doppia 2 ·· = 2
Parto dalla cifra più bassa disponibile (il 4) e imposto l'equazione:
x / 99 + 4 / 9 = 2 => x = 154
da 154 sottraggo le possibili combinazioni a due a due delle cifre rimaste disponibili (9, 7, 6, 5), nel rispetto delle regole date:
154 – 97 = 57 NO
154 – 96 = 58 NO
154 – 95 = 59 NO
154 – 79 = 75 NO
154 – 76 = 78 NO
154 – 75 = 79 NO
154 – 69 = 85 NO
154 – 67 = 87 NO
154 – 65 = 89 NO
154 – 59 = 95 NO
154 – 57 = 97 NO
154 – 56 = 98 NO
Vado avanti e imposto una nuova equazione:
x / 99 + 5 / 9 = 2 => x = 143
da 143 sottraggo le possibili combinazioni a due a due delle cifre rimaste disponibili (9, 7, 6, 4), nel rispetto delle regole date:
143 – 97 = 46 OK 5 / 9 + 97 / 99 + 46 / 99 = 2 .5· + .97·· + .46·· = 2
143 – 96 = 47 OK 5 / 9 + 96 / 99 + 47 / 99 = 2 .5· + .96·· + .47·· = 2
143 – 94 = 49 NO
143 – 79 = 64 OK 5 / 9 + 79 / 99 + 64 / 99 = 2 .5· + .79·· + .64·· = 2
143 – 76 = 67 NO
143 – 74 = 69 OK 5 / 9 + 74 / 99 + 69 / 99 = 2 .5· + .74·· + .69·· = 2
143 – 49 = 94 NO
143 – 47 = 96 OK (come sopra)
143 – 46 = 97 OK (come sopra)
Come si può notare, la somma delle cifre doppie varia in ragione di 11 man mano che si procede ad isolare la cifra singola, infatti il passo successivo porta ad impostare l’equazione come:
x / 99 + 6 / 9 = 2 => x = 132
Ora, considerando la combinazione di cifre a due con 4 decine (tra 9, 7, 5, 4)
132 – 45 = 87 NO
132 – 47 = 85 NO
132 – 49 = 83 NO
Nell’ultima sottrazione appare il numero 3 che è fuori range, allora le altre combinazioni possibili (con 5, 7, 9 decine) non andranno bene sicuramente perché di valore maggiore rispetto ai numeri con 4 decine.
Probabilmente ci si può fermare qui.
ricordo che .5./9 = .5.5./99 ...
Paolo controlla bene i tuoi risultati...
Non saprei Enzo l'unica cosa che mi viene in mente è che i risultati sono almeno 4.
Ossia se 80+ .79 (79 periodico) + .64 (64 periodico) + .5 (5 periodico) = 81.999999999999
Incolonnando i numeri per fare la somma se inverto la seconda cifra dei numeri periodici il risultato non cambia ( il 5 si ripete sempre):
80 + .74 (74 periodico) + .69 (69 periodico) +.5 (5 periodico) = 81.99999999999999
D'altronde sia la prima colonna dei numeri periodi 7+6+5 = 18, sia la seconda 4+9+5 =18, per cui anche invertendo le due colonne il risultato non cambia:
80 + .97 (97 periodico) +.46 (46 periodico) + .5 (5 periodico) = 81.99999999999999
O anche:
80 + .96 (96 periodico) + .47 (47 periodico) + .5 (5 periodico) = 81.99999999999
Magari sto sbagliando, ma a me sembra funzionare.... dove sbaglio?
Non sbagli Paolo, solo che se scrivessi i numeri periodici come frazioni otterresti esattamente 82. Volevo dire solo quello... Dai, che fai parte dei pochissimi su milioni.
Gulp, scusa l'ignoranza
, ma è che non so farlo... dovrei inventarmelo o vedere in rete la relazione tra numero periodico e frazione.
Ok ho visto in rete come si fa...
Quindi:
80 + 79/99 + 64/99 + 5/9 = 80 + 143/99 + 5/9 = 80 + (143+55)/99 = 80 +198/99 = 82
80+ 74/99 + 69/99 + 5/9 = 80 + 143/99 +5/9 = 80 + (143+55)/99 = 80 +198/99 = 82
80 + 97/99 + 46/99 + 5/9 = 80 + 143/99 +5/9 = 80 + (143+55)/99 = 80 +198/99 = 82
80 + 96/99 + 47/99 + 5/9 = 80 + 143/99 +5/9 = 80 + (143+55)/99 = 80 +198/99 = 82