Un problemino non certo difficile, ma che comporta una buona dose di ragionamento e di ... fantasia.
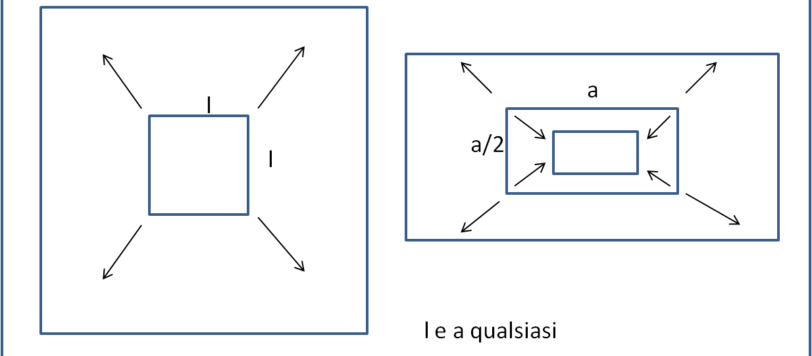

Un problemino non certo difficile, ma che comporta una buona dose di ragionamento e di ... fantasia.

Leggo sull'enciclopedia Treccani che ancora oggi la parola "rutto" dovrebbe essere vietata in quanto sconveniente... tuttavia, non esistono sinonimi equivalenti e proprio l'osservazione di questo fenomeno potrebbe risolvere l'enigma dei buchi neri di stazza intermedia, perciò permettetemi di usarla...

Il titolo farebbe pensare a pianeti come Saturno. E, invece, parliamo di binarie a raggi X che si mostrano attraverso una serie di anelli concentrici.

Conosciamo già le "nove" e, in particolare, quelle ricorrenti. Bene, ve n'è una che si mostra nel suo fulgore e raggiunge una magnitudine di poco meno di 5 mag., per cui è visibile a occhio nudo in ottime condizioni di cielo. Comunque, meglio usare un binocolo o un telescopio di poche pretese.

Archimede ha sicuramente pensato e fatto di tutto e di più. Alcuni suoi principi sono ben conosciuti, altre sue deduzioni molto meno. Occupiamoci di loro e vedremo che Archimede può giustamente essere chiamato il "re dei cerchi".
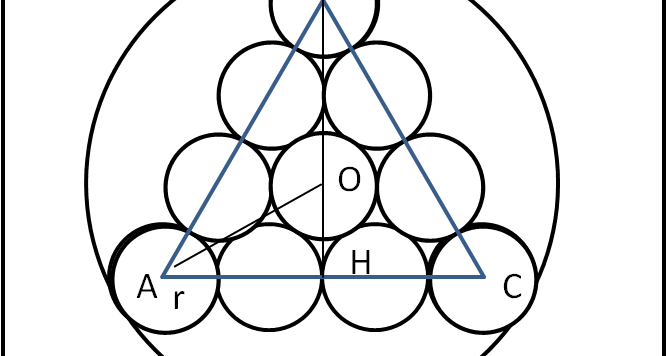
Ottimo Andy e anche Albertone, anche se alla fine vuole trovare r e non l'area minima... Riporto comunque una soluzione decisamente semplice, che rispecchia quelle proposte dai nostri amici.

Continuiamo il nostro racconto storico-scientifico del percorso che ha portato ad una determinazione sempre più accurata della distanza della Terra dal Sole, la cosiddetta Unità Astronomica. Questa volta ci soffermeremo su un episodio che niente ha aggiunto alla conoscenza del nostro Sistema Solare, ma non per questo può essere considerato poco importante. Vediamo perché...
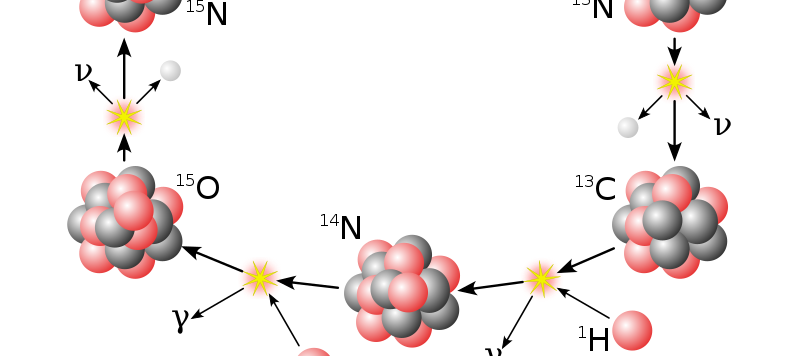
Questo articolo è una breve aggiunta a quello dedicato all'ipotetica popolazione primigenia delle quasi-stelle.
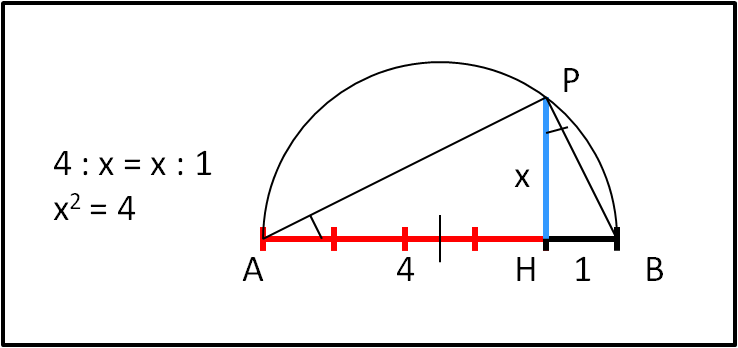
La geometria quasi sacra dei greci continua a stupirci, anche se spesso viene trascurata...
La news è reale e anche interessante, ma, durante questo periodo di minimo per il blog è ammesso condirla in modo scherzoso (sempre che di scherzo si tratti...).
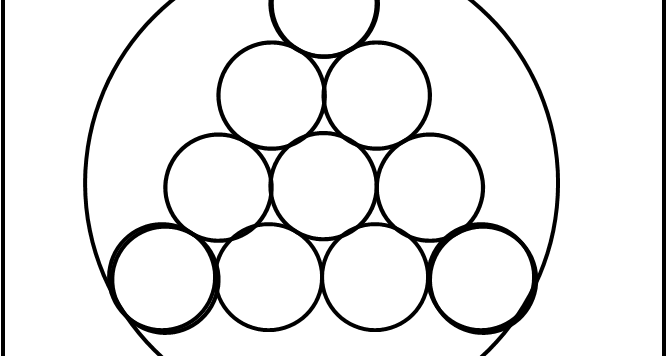
Il problemino non è certo difficile, ma tra i tanti modi per risolverlo ve n'è uno che mi piace particolarmente. Pensate che nel 1812 è stato proposto, in Giappone, agli studenti di 15 anni. Che dite di riproporlo oggi? Abbiate pazienza, ma esercizi più difficili li vorrei lasciare per il "dopo-ferie".