Categorie: Matematica
Tags: goemetria iperbole paradosso solidi di rotazione tromba di Gabriele tromba di Torricelli
Scritto da: Vincenzo Zappalà
Commenti:3
Il paradosso del pittore **
Un paradosso che ancora mantiene il suo fascino.
Abbiamo trattato molti paradossi nel nostro Circolo, a partire da quelli più classici e famosi di Zenone (QUI, QUI e QUI). La maggior parte di questi sono stati risolti con l'applicazione del concetto di limite, ma, alcuni sembrano resistere ancora oggi, con tutta la matematica più sofisticata di cui si è ormai padroni. In realtà, una spiegazione c'è sempre, ma abbisogna di una matematica molto sottile. Affrontiamo, perciò, il paradosso del pittore o della tromba di Gabriele (inteso come angelo...). Detto in parole molto spicce potremmo riassumerlo come segue:
"Prendiamo un vaso qualsiasi abbastanza ampio e riempiamolo di vernice. Ebbene si dimostra che la vernice sufficiente a riempire il vaso NON è sufficiente a dipingere la superficie esterna del vaso". Cosa che appare del tutto incredibile e paradossale.
L'ideatore di questa strana "tromba" è Evangelista Torricelli (1608-1647) che con il suo paradosso sollevò un mare di dispute e di controversie e ancora oggi non tutti sono convinti che esista una soluzione puramente matematica che risolva l'assurdità del risultato. Molto più semplice ne è una spiegazione "fisica", che non era ovviamente possibile ai tempi del Torricelli. Egli descrive la sua "tromba" come "solido iperbolico acutissimo".

In realtà, il vaso ha una forma un po' strana e ha il vantaggio di essere ... infinito. Cerchiamo di disegnare questo vaso utilizzando una curva a noi ben nota: l'iperbole nella forma y = 1/x. Disegniamola nel piano (x,y) e poi facciamola ruotar attorno all'asse x, ottenendo un solido di rotazione che ha effettivamente la forma di una tromba del giudizio. Tagliamola con il piano perpendicolare a x passante per x = 1 e la tromba diventa praticamente perfetta. Avete già capito che questa tromba ha una caratteristica piuttosto strana: si sa dove comincia, ma non si sa dove finisce. In altre parole essa si rastrema sempre più per x che tende all'infinito.

Bene, adesso chiediamo a un valente pittore di dipingere di colore argenteo l'esterno della tromba. Per essere magnanimi gli mettiamo a disposizione tutta la vernice che la tromba riesce a contenere. Una quantità FINITA che appare più che sufficiente allo scopo. E, invece, il risultato è negativo... La vernice non basta assolutamente a colorare la parte esterna e per quanta gliene fornissimo, il pittore dovrebbe lasciare l'opera incompiuta. Ricordiamo, però, che è stato possibile riempire completamente la tromba di vernice (e, quindi, la sua parte interna).
Bene... questo è un vero e proprio paradosso che ha dell'incredibile! Abbiamo un solido di rotazione che si assottiglia sempre di più, ma non termina mai, e questo comporta che esso può essere riempito perfettamente da una quantità finita e calcolabile di vernice, ma non può essere mai verniciato esternamente. Non ci resta che dimostrare matematicamente che questo "strano" e paradossale risultato è confortato dalla matematica odierna, con tanto di integrali.
Iniziamo con il calcolo del volume interno, quello che ci dice la quantità di vernice che può essere contenuta nello "strumento".
Calcolo del volume interno
Consideriamo una certa y = f(x) come curva sul piano (x,y) a facciamola ruotare attorno all'asse x. Otteniamo così un solido di rotazione.
Il volume totale non è altro che la somma di sottilissimi volumetti cilindrici che abbiano altezze pari a un valore dx estremamente piccolo (metodo dei dischi) (Fig. 2).

Ogni cilindretto ha quindi un volume pari a πr2 dx. Cosa scegliamo come valore del raggio r? Beh, il valore "medio " del cilindretto che altri non è che la y corrispondente. Nel nostro caso y =1/x (iperbole). Il volume totale del nostro solido di rotazione sarà quindi dato dalla sommatoria (integrale), tra il valore iniziale di x e quello finale, della quantità π/x2 dx. Nel caso della tromba di Gabriele il valore iniziale di x è uguale a 1 e quello finale è ∞, perciò:
V = ∫1∞ π/x2 dx
Questo integrale è facilissimo da calcolare (1/x2 è la derivata di - 1/x) e porta al risultato:
V = π [- 1/x]1∞ = π[-1/∞ - (- 1/1)] = π[0 + (1/1)] = π
Il volume totale è, quindi, FINITO e vale π.
Il che vuole anche dire che si riesce sicuramente a dipingere la superficie interna, avanzando parecchia tinta.
Calcolo della superficie esterna.
L'espressione da integrare deve tenere conto che la superficie esterna di un tronco di cono, pur piccolo a piacere, deve essere una striscietta. In altre parole il tronchetto di cono infinitesimo dipende sia dal raggio iniziale che da quello finale. La formula ben nota che la determina è data dalla somma dei raggi iniziale e finale moltiplicata per l'apotema a. Quanto vale il segmento a? Basta considerare il teorema di Pitagora applicato alla Fig. 3.

Ne segue che
a = √(dx2 + dy2) = dx√( 1 + (dy/dx)2)
La formula finale della superficie esterna del tronchetto di cono è quindi data da:
dS = π (yi + yi+1)√( 1 + (dy/dx)2)dx
Per valori molto piccoli di dx, possiamo considerare dy/dx la derivata di f(x) rispetto a x, mentre y i +1 = yi = y = f(x). La formula diventa, quindi:
dS = 2π f(x)√( 1 + f '(x)2)dx
Nel nostro caso si ha:
dS = 2π/x √((1 + (- 1/x2)2)
dS = 2π/x dx √(1 + 1/x4)
S = ∫1∞2π/x √(1 + 1/x4)) dx .... (1)
Beh... questo non è un integrale molto facile, ma possiamo ricordarci una semplice regola: se una certa espressione è uguale a infinito, qualsiasi espressione che sia maggiore di essa deve valere infinito.
Nel nostro caso, per qualsiasi valore di x, grande a piacere,
1 + 1/x4 ≥ 1
Ne segue che S deve essere maggiore di ∫1∞ 2π/x dx (abbiamo considerato il valore minimo di 1 + 1/x4). Ma se questo integrale fosse infinito lo sarebbe a maggior ragione l'espressione (1) che è sicuramente più grande o, al limite, uguale...
Consideriamo, allora, il ben più semplice integrale
∫1∞ 2π/x dx = 2π∫1∞ dx/x
Esso vale
2π∫1∞ dx/x = 2π [ln x]1∞ = 2π [∞ - 0] = ∞
da cui
S risulta maggiore o uguale di un qualcosa che vale infinito e quindi deve valere sicuramente infinito!
Fino a qui abbiamo applicato le formule classiche pet la determinazione del volume e della superficie esterna di un solido di rotazione. Tuttavia, per chi volesse essere più sbrigativo (anche se un po' rozzo) possiamo pensare al volume finale come alla somma di tanti cerchietti di area π y2 = π /x2, mentre la superficie finale è la somma di tante circonferenze di raggio y, ossia 2π/x
Esse individuano due serie armoniche. Per il volume vale
∑1∞ π (1/x2) = π ∑1∞ (1/x2) = valore FINITO (serie convergente)
Per la superficie vale:
2π ∑1∞ (1/x) = INFINITO (serie divergente)
A parte i valori numerici il paradosso viene comunque dimostrato.
E' un vero paradosso?
Le idee, a riguardo, non sono omogenee. C'è chi continua a considerarlo un paradosso perfetto, mentre altri vedono varie motivazioni per non considerarlo tale.
Da un punto di vista puramente matematico, ad esempio, gioca il fatto che la "tromba" viene considerata solo a partire da x = 1. Se venisse, invece, considerata nella sua interezza, ossia a partire dal valore x = 0, l'intero paradosso cadrebbe dato che anche il volume andrebbe a infinito.
Da un punto di vista fisico, la soluzione è sicuramente più semplice e logica. La vernice è composta di granuli, per piccoli che siano, da cui segue che continuando a inserirli all'interno della tromba, prima o poi il diametro dei granelli sarebbe superiore al diametro della tromba e la vernice non potrebbe andare oltre, mentre verniciandolo dalla parte esterna non ci sarebbe limite al diametro dei granelli.
Comunque sia, il problema, anche oggi che la matematica sembra non avere più problemi, la tromba non perde sicuramente il suo fascino...






3 commenti
Secondo me è un limite degli integrali alla Riemann. Se si usa Stieltjes , calcolando l'area di 1/x^2 tra 0 e 1 (meno 1 ) si ottiene infinito , coerentemente con gli esiti attesi.
Il poradosso si è considerato dimostrato mostrando che il volume del solido ideale, che è il volume della vernice, è finito, mentre la sua superficie, che è la superficie da verniciare, è infinita.
Implicitamente si è dato per scontato che un volume finito di vernice non possa coprire una superficie infinita. Ma questo non è vero. Almeno non è vero con lo stesso livello di idealizzazione con il quale si è considerato il solido.
Cerco di quantificare quanto detto nel commento sopra. Immagino di verniciare la superficie esterna del solido con uno strato di vernice di spessore uguale o inferiore ad 1/10 del raggio in quel punto.
In figura una sezione della tromba con lo strato di vernice.
Per calcolare il volume massimo di vernice necessario posso fare la differenza tra il volume di un solido di rotazione simile alla tromba generato dalla funzione 1,1/x ed il volume della nostra tromba pari a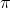 .
.
Calcolando il volume del solido più grande con lo stesso metodo descritto nell'articolo ottengo
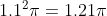
Quindi il volume di vernice necessario è inferiore o uguale a che è minore del volume del solido pari a
che è minore del volume del solido pari a 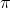
Certo, la vernice che ipotizzo di utilizzare è ideale, ma anche il solido che devo verniciare è ideale.
Se il raggio del tubo della tromba può tendere a zero in modo continuo, devo assumere che possa farlo anche lo strato di vernice. Se così non fosse il paradosso cadrebbe comunque. È evidente che se il raggio della tromba può tendere a 0, mentre lo strato di vernice deve rimanere di spessore costante ben presto il volume interno diventerebbe minore del volume dello strato di vernice.
A mio parere il paradosso non esiste. L’impressione che ci sia un paradosso nasce dall’avere paragonato una superficie con un volume ed avere assunto impropriamente che una superficie infinita non possa essere ricoperta da un volume finito. Se paragoniamo volumi con volumi, grandezze omogenee, il paradosso non appare.