Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"

Mi spiace che nessuno abbia provato a risolvere questo "problema" che ci riporta alla Scuola d'Atene. Io trovo queste antiche costruzioni veramente interessanti e istruttive. Riporto, perciò, tutti i passaggi.

Consideriamo un'ellisse qualsiasi ottenuta, ad esempio, tagliando un cono con un piano inclinato. Sia quella di Fig. 1.

Per prima cosa, dobbiamo determinare il centro O dell'ellisse. Andiamo per gradi e tracciamo una corda qualsiasi AP dell'ellisse, come mostra la Fig. 2.

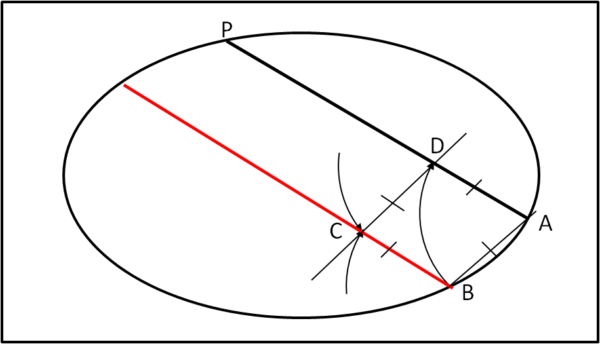
A questo punto vogliamo  tracciare una parallela ad AP da un qualsiasi altro punto B dell'ellisse. Il gioco è abbastanza semplice... Con centro in A tracciamo la circonferenza di raggio AB mediante il compasso. Determiniamo un punto D sulla retta AP. Ovviamente, per costruzione AB = DA. Con centro in B e in D tracciamo due circonferenze di raggio BA = DA.

Le due circonferenze si intersecano nel punto C. Non rimane che congiungere B con C e prolungarlo per ottenere una corda parallela ad AP. Si dimostra facilmente che la retta BC è parallela ad AP. Per costruzione BA = DA, ma anche BC = DC. Avevamo però scelto BC = BA (e DC = DA), da cui AB = BC = DC = AD. Ne segue che il quadrilatero ABCD è un rombo (quattro lati uguali) e, di conseguenza, i suoi lati sono paralleli a due a due. Lo sono, perciò, anche BC e AD.

In poche parole abbiamo tracciato due (o più) corde dell'ellisse parallele tra di loro. A questo punto determiniamo il loro punto di mezzo. Mostriamo la costruzione solo per la corda AB di Fig. 3.

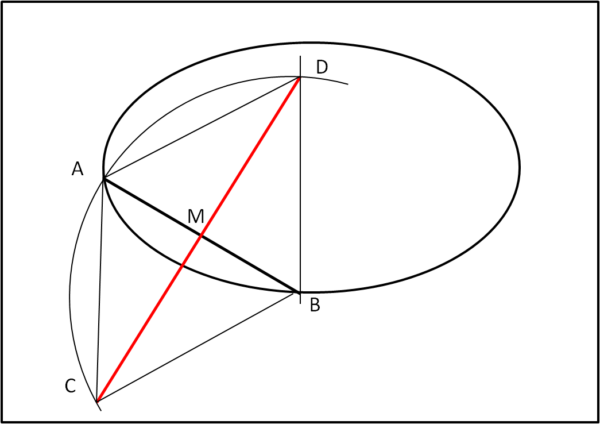
Basta tracciare le circonferenze di centro in A e in B che abbiano raggio AB. Esse si incontrano nel punto C e nel punto D. C e D sono equidistanti da A e da B per costruzione e, di conseguenza, il segmento CD è l'asse di AB. L'intersezione con esso permette di determinare il punto medio M.

Ripetiamo lo stesso procedimento par una  corda parallela ad AB (o più). Tracciamo poi un'altra corda qualsiasi PQ e, dopo aver determinato una sua qualsiasi parallela, determiniamo come prima i loro punti medi. Non ci rimane che ricordare una proprietà dell'ellisse: si chiama diametro di un ellisse ogni corda che passi per il punto medio di una fascio di corde parallele. Ogni diametro passa per il centro O dell'ellisse. In Fig. 4, abbiamo rappresentato la retta descritta dai punti medi di quattro rette parallele a due a due. L'intersezione delle rette che passano per i loro punti medi individuano il centro O dell'ellisse.

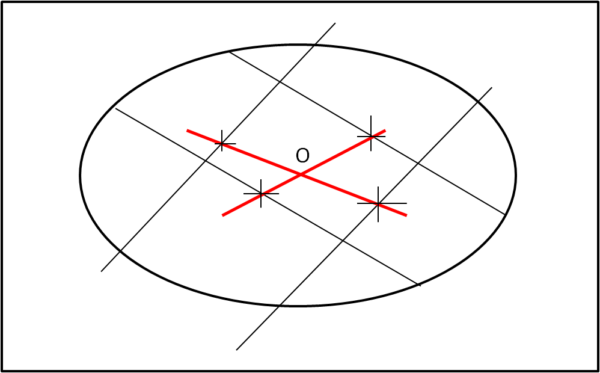
Siamo a buon punto. Passiamo ora alla determinazione degli assi dell'ellisse. Operazione molto facile... Facendo centro in O tracciamo una circonferenza che intersechi in quattro punti l'ellisse. Determiniamo immediatamente il rettangolo ABCD e, come già fatto precedentemente, i punti medi dei 4 lati. Tracciamo le due rette che passano per i punti medi. Abbiamo così due diametri che sono tra di loro perpendicolari per costruzione. Per simmetria essi devono anche essere il diametro massimo e quello minimo (ricordiamo che un diametro deve passare per il centro O). AO e BO sono i semiasse desiderati (Fig. 5).

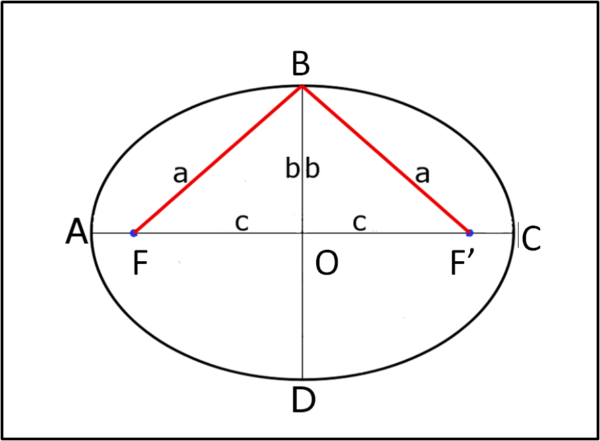
Siamo giunti al punto critico. Nei vari (pochi) siti che ho trovato, si dice che ora basta aprire il compasso del semiasse maggiore a e tracciare una circonferenza di tale raggio che abbia centro in P. L'intersezione di questa circonferenza con il semiassi AO determina la posizione di un fuoco F. Analoga costruzione per il fuoco F'. Questa conclusione è esatta. Il punto B (il precedente P) deve distare dai due fuochi proprio una distanza pari al semiasse a (l'ellisse è il luogo dei punti la cui distanza dai due fuochi è costante) dato che BF + BF' = 2a e BF = BF'. In poche parole, si ha (teorema di Pitagora)  OF² + b² = a². Questa relazione è valida solo se OF è la distanza tra fuoco e centro dell'ellisse (Fig. 6).

La costruzione, però, NON E' LECITA, dato che abbiamo trasportato in B il segmento a, ossia abbiamo utilizzato il compasso come "riga graduata". Il compasso della Scuola d'Atene può solo tracciare un cerchio che tra due punti già determinati e non può trasportare un raggio prefissato. Per fortuna ci viene in aiuto ancora Euclide che ci insegna come trasportare un certo segmento in un'altra posizione (con riga e compasso perfettamente utilizzati). Mostriamolo in Fig. 7.

Ciò che dobbiamo fare è trasportare il segmento OA (semiasse maggiore) in B.  Poi, tracciando la circonferenza di raggio uguale ad a, si individua su AO il fuoco F.  Euclide ci aiuta mediante un metodo "perfetto", di grande semplicità ed arguzia. Con centro in O e in B tracciamo due circonferenze di raggio OB. Esse si incontrano nel punto S. Prolunghiamo i segmenti  SO e SB, che sono uguali tra loro per costruzione. Facendo centro in O tracciamo la circonferenza di raggio OA che incontra la retta SO in R. Notiamo che, agendo in questo modo, OR è uguale al semiasse OA. Non ci resta che fare centro in S e tracciare la circonferenza di raggio SR. Essa incontra la retta SB in T. Il nostro "trasporto" si è praticamente concluso dato che ST = SR e, quindi, anche BT = OR = OA. Facendo centro in B tracciamo, infine, la circonferenza di raggio BT fino a incontrare il semiasse AO in F.

La nostra costruzione è terminata, seguendo le regole perfette della Scuola di Atene.