A cosa si riferiscono le due date del titolo? Al teorema di Pitagora e in particolare a due "nuovi" metodi usati per dimostrarlo.

Due personalità famose a confronto. Uno è il grande Einstein, l'altro un Presidente degli Stati Uniti, James A. Garfield, rimasto in carica solo pochi mesi, dal marzo al luglio 1881, in quanto vittima di un attentato (morì due mesi dopo). Cosa possono avere in comune? Il semplice fatto che entrambi hanno ideato un nuovo metodo per dimostrare il teorema di Pitagora.

Il celebre teorema è stato dimostrato in decine di modi diversi, ma è interessante vedere come il grande fisico riuscì a compiere l'impresa a soli 12 anni. Di contro, un Presidente, laureato in legge, ma amante di greco e latino (li ha anche insegnati), che ottenne celebrità anche per la sua brillante dimostrazione. Il primo utilizza la similitudine tra triangoli e il secondo un trapezio. Vale la pena richiamarli, dato che l'età del primo chiarisce una volta di più, se ce ne fosse ancora bisogno, la falsa idea (fakenews ...) che Albert fosse "scarso" in matematica (i voti in Svizzera andavano solo fino al 6 e lui aveva proprio 6).

L'abilità del secondo mostra una mente molto brillante, interessata a tutto ciò che lo circondava (i migliori muoiono sempre giovani).

 

La dimostrazione di Einstein

Consideriamo un triangolo rettangolo qualsiasi ABC, in Fig. 1, e tracciamo da C  l'altezza relativa all'ipotenusa AB, che viene toccata in D. Definiamo anche con a, b, c la lunghezza dei tre lati  BC, AC e AB.

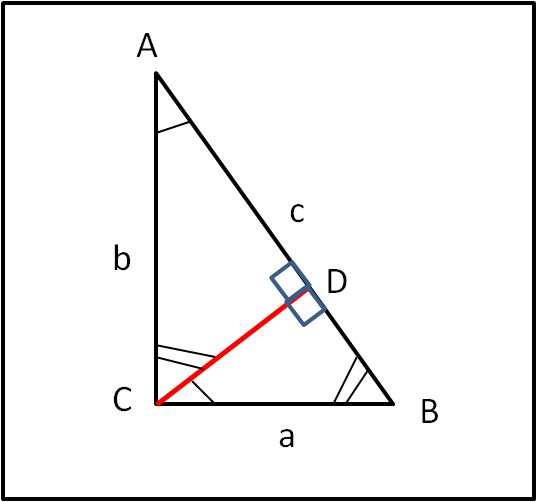
Risulta subito che i tre triangoli ACB, ADC e BDC sono simili tra loro (due angoli uguali perché uno è retto e l'altro è complementare di uno stesso angolo). Possiamo, allora, scrivere delle semplici proporzioni:

BD/DC= a/b

DC/AD = a/b

Da cui:

BD = a/b DC

AD = b/a DC

Scriviamo l'area del triangolo di partenza come somma delle aree dei due triangoli simili più piccoli:

1/2 AC BC = 1/2 AD DC + 1/2 DB BC

1/2 ab = 1/2 b/a DC² + 1/2 a/b DC²

ab = (a/b + b/a) DC²

Moltiplichiamo entrambi i membri per ab

a²b² = (a² + b²) DC²

Da cui

DC² = a²b²/(a² + b²)

Ma, dalla Fig. 1, abbiamo che:

c = DB + AD  = a/b DC + b/a DC = DC (a/b + b/a) = DC (a² + b²)/ab

c² = DC² (a² + b²)²/a²b²

Sostituendo il valore di DC²   ottenuto prima:

c² = a²b² (a² + b²)²/(a²b² (a² + b²))

semplificando...

c² = a² + b²

C.V.D.

 

La dimostrazione di Garfield

Consideriamo lo stesso triangolo ABC di prima, lo duplichiamo in A'B'C' e lo giriamo di 90° portando B' a coincidere con A, come mostrato in Fig. 2. Uniamo, poi, A' con B.

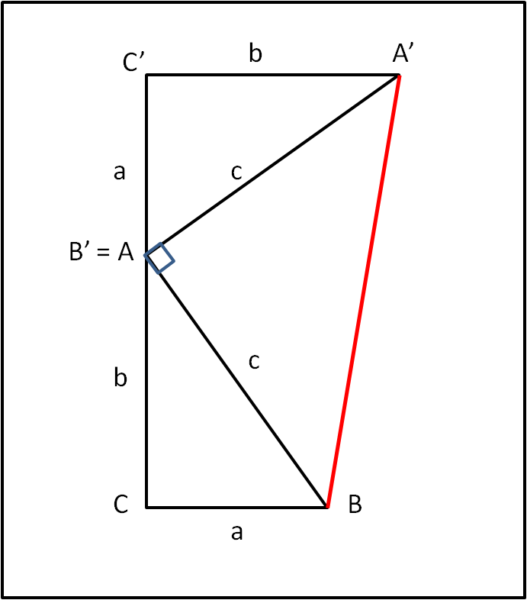
Si ottiene un trapezio rettangolo. La somma degli angoli C'AA' e CAB è 90° e 9o° deve anche essere l'angolo A'AB.

Calcoliamo l'area del trapezio in due modi:

1)     Somma delle basi per altezza diviso 2

A_CC'AB = 1/2 (a + b)(a + b) = 1/2 (a + b)²

2)    Somma delle aree dei tre triangoli  ACB, A'C'B' e A'AB

A_CC'AB = 1/2(ab) + 1/2(ab) + 1/2 c²

Uguagliamo le due aree semplificando il fattore 1/2

(a + b)² = 2 ab + c²

a² + b² + 2 ab = 2 ab + c²

a² + b² = c²

C.V.D.

Che dire? Forse, forse... Garfield batte Einstein (dodicenne) per rapidità ed eleganza!

 

QUI il teorema di Pitagora dimostrato al contrario