Com'era facile intuire, la soluzione al quiz sull'esagono diventa quasi immediata ricordando le aree dotate di segno. Comunque un grazie ad Artù e Fabry per le loro soluzioni alternative!

Disegniamo il nostro esagono  ABCDEF. Fondamentale è ricordarsi che vale l'enunciato:

Preso un punto P qualsiasi, interno od esterno a un triangolo ABC, l'area del triangolo può essere sempre scritta come:

S(ABC) = S(PAB) + S(PBC) + S(PCA)

Dove S indica che l'area è presa con segno, ossia rispettando la rotazione antioraria.

In Fig. 1 consideriamo i triangoli ABE e ABD. Essi hanno la stessa area, dato che hanno la stessa base (AB) e la stessa altezza h1 (AB è parallela a DE)

Possiamo scrivere:

S(ABE) = S(ABD)

In Fig. 2 consideriamo, invece i triangoli EFB ed EFC.

Per la stessa ragione dei due precedenti, vale anche :

S(EFC) = S(EFB)

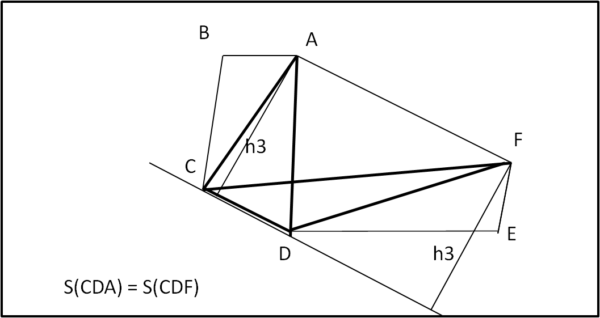
Infine consideriamo i triangoli  CDA e CDF (Fig. 3). Ancora una volta possiamo scrivere:

S(CDA) = S(CDF)

Esprimiamo ogni area in funzione di un punto P qualsiasi (ma uguale per tutte), seguendo l'enunciato precedente:

S(ABE) = S(ABD)

S(PAB) + S(PBE) + S(PEA) = S(PAB) + S(PAB) + S(PBD) + PDA)

semplificando

S(PBE) + S(PEA) =  S(PBD) + S(PDA)             ... (1a)

 

S(EFC) = S(EFB)

S(PEF) + S(PFC) + S(PCE) = S(PEF) + S(PFB) + S(PBE)

semplificando

S(PFC) + S(PCE) = S(PFB) + S(PBE)                       .... (1b)

 

S(CDA) = S(CDF)

S(PCD) + S(PDA) + S(PAC) = S(PCD) + S(PDF) + S(PFC)

semplificando

S(PDA) + S(PAC) = S(PDF) + S(PFC)                    .... (1c)

 

Sommiamo (1a), (1b) e (1c)

S(PBE) + S(PEA) + S(PFC)  + S(PCE) + S(PDA) + S(PAC) = S(PBD) + S(PDA) + S(PFB) + S(PBE)+ S(PDF)  + S(PFC)

semplificando

S(PEA) + S(PCE) + S(PAC) = S(PBD) + S(PFB) + S(PDF)

Sempre per l'enunciato, il primo membro può essere scritto come:

S(PEA) + S(PCE) + S(PAC) = S(ACE)

Il secondo come:

S(PBD) + S(PFB) + S(PDF) = S(BDF)

Per cui

S(ACE) = S(BDF)

Che equivale, dato che il verso è antiorario, a concludere che

A(ACE) = A(BDF)

C.V.D.