Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

 

Vogliamo cercare di rendere più semplice possibile il tentativo di gettare un sasso in modo che riesca ad arrivare il più lontano possibile. Per riuscirci, utilizziamo un semplice metodo basato sulla geometria e su un pizzico di fisica classica.

Se il punto di partenza e di arrivo sono alla stessa altezza, sappiamo già che inclinazione dobbiamo dare alla velocità di lancio perché ciò si ottenga: basta lanciare con una velocità la cui direzione formi un angolo di 45° con il suolo. Tuttavia, se il sasso viene lanciato da una certa altezza, la faccenda si complica... Vediamo cosa capita in Fig. 1, dove sono disegnate due traiettorie: quella relativa a un lancio di 45° e quella relativa a un lancio con inclinazione minore. Il tutto, ovviamente, a parità di modulo della velocità.

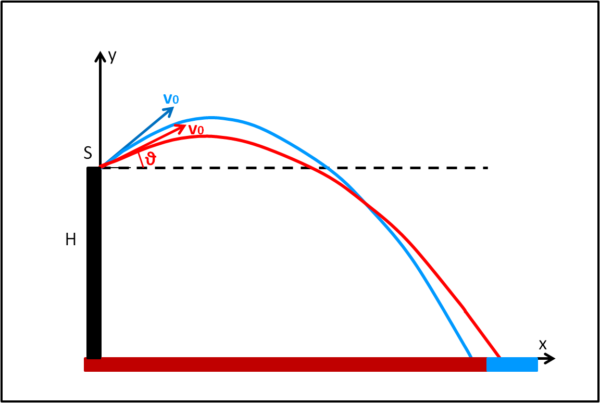
L'altezza del lancio sia H (in cima a un grattacielo o a una torre) e la velocità di lancio sia v₀. Se l'angolo θ è di 45° (traiettoria azzurra) il lancio darà luogo alla massima distanza lungo la parallela all'asse x, tracciata dal punto O di lancio. Ma se la gittata massima è relativa al suolo (asse x), la traiettoria rossa necessita di un angolo di lancio minore di 45°.

Come fare a stabilire se è possibile lanciare il sasso da un'altezza H, con una certa velocità v₀, in grado di raggiungere o superare una certa distanza d, conosciuta ?

Facciamo un esempio molto pratico. Il signor S è incaricato di raggiunge la cima di una torre, che è alta proprio H. Ha a disposizione un piccolo cannone che gli permette di lanciare un certo oggetto con una certa velocità v₀ e che gli permette di imporre un certo angolo al cannone. La torre si trova a una certa distanza d da un lago, in cui un suo amico aspetta di ricevere proprio l'oggetto in questione. L'amico gli ha detto che per riuscire a lanciare fino al lago  è necessario che lanci proprio con l'angolo relativo alla massima distanza raggiungibile. Ne consegue che il signor S deve calcolare, in base alle condizioni di partenza, l'angolo di massima gittata, altrimenti l'oggetto non cadrà in acqua e si romperà.  Non chiedetemi che oggetto è e perché deve giungere proprio in acqua... probabilmente c'è dietro una storia di spionaggio!

Siamo di fronte, ovviamente, a un tipico esempio di moto parabolico. Non è la prima volta che lo trattiamo, anche in modo piuttosto complicato (QUI) e quindi prendiamo per buone le leggi orarie del moto in questione (il tutto viene anche esaurientemente spiegato  nel libro "La Fisica addormentata nel Bosco").

Metodo "classico"

In breve, noi siamo di fronte alla composizione di due moti: uno rettilineo uniforme con velocità orizzontale (parallelo all'asse x) e uno uniformemente accelerato (anzi decelerato) che avviene lungo l'asse verticale y. La combinazione dei due moti dà il classico moto parabolico nel piano xy. Le due velocità introdotte non sono altro che le componenti lungo x e lungo y della velocità iniziale v₀ (ossia quella di lancio). Rappresentiamo il tutto in Fig. 2.

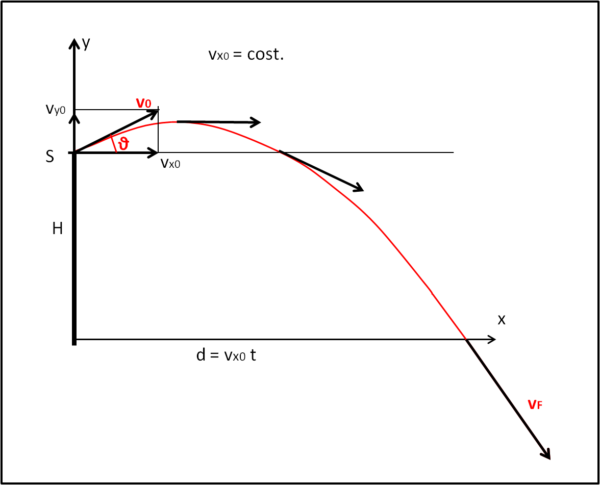
Riprendiamo le formule che esprimono le leggi orarie dei due moti, considerando che il punto di origine S ha coordinate x₀ = 0 e y₀ = H:

x =  v_0x t                                         .... (1)

y = H + v_0y t - 1/2 gt²                   .... (2)

Noi vogliamo sapere che angolo θ è in grado di dare la massima gittata. Solo così il nostro signor S saprà di aver ottenuto il massimo possibile.

La prima equazione (1) è in grado di darci il valore che vogliamo, ma bisogna conoscere il tempo t. Lo ricaviamo dalla (2), dopo aver scritto v_0y in funzione dell'angolo θ e del valore della velocità v0.

y = H + (v₀ sinθ) t - 1/2 gt²

Questa è un'equazione di secondo grado che ci permette di ricavare t. Accettiamo l'unica soluzione valida...

t = (1/g)((v₀ sinθ) t + √((v₀sinθ)² + 2gH))

e la andiamo a inserire nella equazione (1) che dà il moto rettilineo uniforme:

x = (v₀ cosθ/g)((v₀ sinθ) t + √((v₀sinθ)² + 2gH))

Questo è il valore della gittata. Non ci resta che eseguire la sua derivata e uguagliarla a zero in modo da ottenere l'angolo θ, che corrisponde al massimo valore d della gittata.

dx/dt = v_o/g (-sinθ (v₀ sinθ + √((v_o sinθ)² + 2gH)) + cosθ (v₀ cosθ + v_o² sinθ cosθ/√((v_o sinθ)² + 2gH)))  = 0

Oh, mamma mia! Un'impresa con poche speranze e comunque fuori dalle capacità del signor S, che ha a sua disposizione solo una calcolatrice vecchio stile che gli regala le 4 operazioni, la radice quadrata, il quadrato e le funzioni trigonometriche con le loro funzioni inverse. Già è per lui operazione insormontabile la soluzione della equazione di secondo grado... Ci vuole qualcosa di più semplice!

Metodo geometrico-fisico

Ragioniamo in termini di velocità. Esse, durante il volo, hanno una componente in direzione verticale variabile, mentre la direzione in senso orizzontale è costante. L'unica velocità che permette di muoversi in questa direzione è, quindi, quella orizzontale uguale a v_ox. Nel tempo totale t di volo, è proprio questa componente che permette di raggiungere una certa distanza d. Ossia:

v_ox = d/t

d = v_ox t                   .... (3)

Passiamo alla componente  verticale. Il vettore velocità cambia continuamente sia in direzione che in modulo. Tuttavia, la sua componente lungo x non cambia, come abbiamo appena visto, per cui, se trasportiamo tutte le velocità acquisite dall'oggetto durante la traiettoria in modo da avere lo stesso punto di applicazione, otteniamo la Fig. 3.

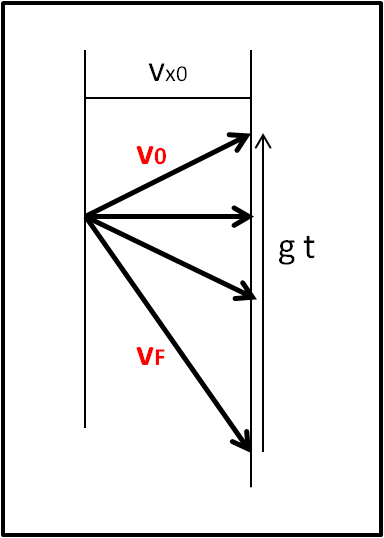
Non ci stupiamo certo che esse siano contenute in un triangolo che ha come lato superiore la velocità iniziale v₀ e come lato inferiore la velocità finale v_F. Quale sarà il terzo lato (quello verticale)? Esso non è altro che il vettore differenza tra v_F e v0. Chi è comanda la variazione di velocità? Nient'altro che l'accelerazione costante g. Per cui, il lato verticale non è altro che gt.

Occupiamoci di questo triangolo, di cui conosciamo i tre lati in funzione del tempo di volo t. Risulta, soprattutto, che non vi è più nessun legame con l'angolo di inclinazione della velocità di partenza. Ciò segue dalla legge di conservazione dell'energia.  Quella posseduta al momento della partenza deve essere uguale a quella finale.

Al momento della partenza abbiamo un'energia cinetica a cui si somma un'energia potenziale che dipende dall'altezza H rispetto all'asse x. Al momento dell'arrivo l' energia è soltanto energia cinetica:

1/2 m v₀²  + m gH = 1/2 mv_F²

da cui si ottiene:

v_F = √(vo² + 2gH)                 .... (4)

Ciò implica che la velocità finale è una costante, dato che lo sono g, H e v_o².

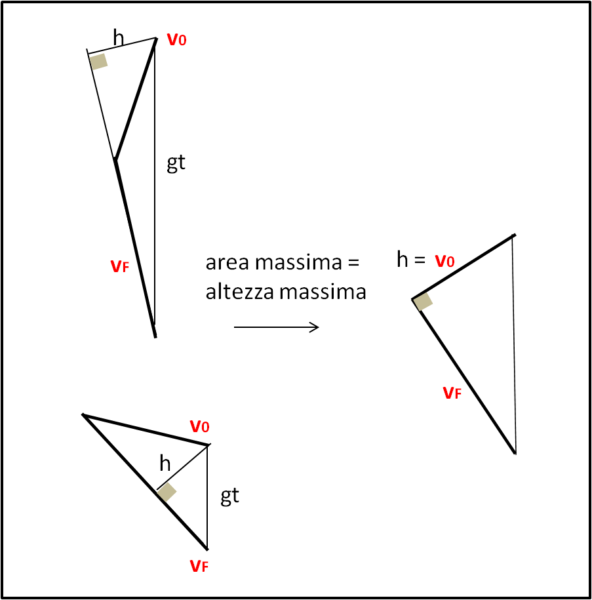
Conosciamo ormai molte cose del triangolo precedente, ma cosa ha a che spartire con la nostra massima gittata? Consideriamo il caso in cui la v₀ sia diretta esattamente verso l'alto. L'area del triangolo si annulla. La stessa cosa capiterebbe se la v₀ fosse diretta esattamente verso il basso, come mostrato a destra di Fig. 4.

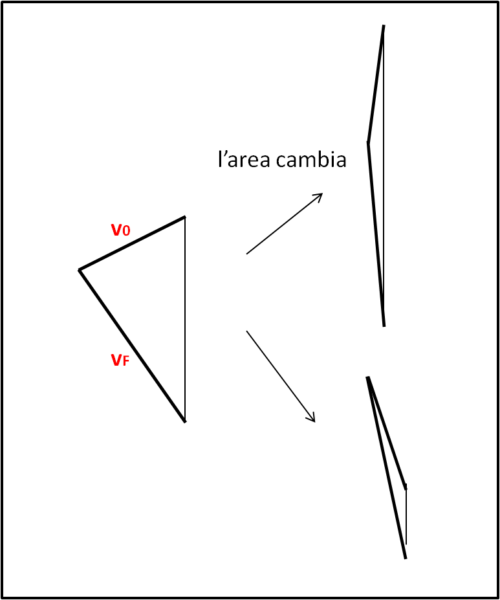
Bene, possiamo intuire che la gittata dipende dall'area A del triangolo: quando essa si annulla si annulla anche la gittata. Proviamo a calcolarla, ricordando che dobbiamo fare il prodotto tra base e altezza e dividerlo per 2, ossia:

A = 1/2 gt v_ox                   .... (5)

Come base abbiamo preso il lato verticale e come altezza la componente orizzontale v_0x del vettore v₀. Ricordiamo, a questo punto, la (3) che ci dice quanto vale v_0xt. Sostituiamo nella (5) e otteniamo:

A = 1/2 g d                      .... (6)

L'area dipende unicamente dal valore di d, dato che g è una costante. Ciò vuol dire che massimizzare la distanza percorsa d vuole dire ottenere la massima area del triangolo. Noi conosciamo il lato inferiore che è uguale alla velocità finale v_F che è una costante. Costruiamo, allora i triangoli che abbiano questo lato fisso e il lato verticale uguale a gt. Considerando gt come base, per massimizzare l'area dobbiamo, allora, massimizzare l'altezza. Ma l'altezza è massima quando risulta uguale proprio a vo (l'altezza è sempre la componente orizzontale di vo ed è massima quando è proprio uguale a v0), come mostra la Fig. 5.

Ciò vuol dire che il il triangolo deve essere rettangolo. In altre parole, la massima gittata si ottiene quando l'angolo tra velocità finale e velocità iniziale è di 90°. Tracciamo la perpendicolare dal punto A al lato verticale BC = gt. Otteniamo un triangolo rettangolo ABK (colorato in rosa) che è simile al triangolo di partenza ABC, dato che sono entrambi rettangoli e hanno l'angolo in B in comune (Fig. 6).

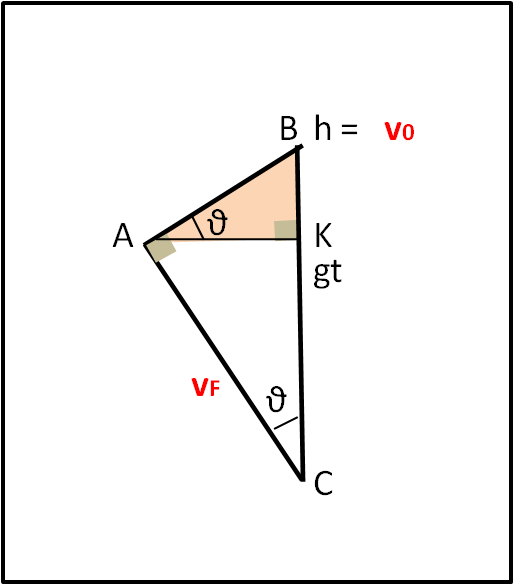
Essendo simili devono avere l'angolo in C uguale, ma questo è proprio l'angolo dell'inclinazione iniziale θ. Questo angolo che ci regala la massima area e quindi la massima gettata. Passando a una formula trigonometrica semplice semplice (la conosce perfino il signor S), possiamo dire che:

tan θ = v_o/v_F

Le due velocità sono ben conosciute e quindi è ben conosciuto l'angolo di massima gittata che risulta essere:

θ = arctan (v_o/v_F)

Il signor Il signor S  è un solenne "asino" in matematica, ma conosce un po' di fisica e di geometria, per cui non ha problemi a calcolare v_F e  qualsiasi piccola calcolatrice possiede la funzione arctan ...

Lui lancia con l'angolo θ trovato e sa di non poter sbagliare il lancio!