Questo articolo è una delle tante "ciliegine cosmiche" che potete gustare QUI

 

Sembra quasi impossibile, ma la solita vecchia domanda continuo a sentirla ripetere. Proviamo a rispondere in modo ultra semplice utilizzando solo un po' di geometria elementare e affidandoci a un vero superastronomo dotato di una tecnologia eccezionale. La sua risposta alla domanda sarà forse, finalmente, accettata da tutti, basandosi soltanto su dati osservativi.

Qual è la domanda? Beh,  la solita...

"Dove si trova il Big Bang nella sfera celeste? Lo potremo vedere in futuro con le tecnologie più sofisticate?"

La risposta, altrettanto solita, non può che essere: "Dovunque" alla prima parte e: "Comunque, non potremmo mai vederlo, dato che le prime fasi dell'Universo non emettevano luce".

La seconda parte della risposta soddisfa quasi sempre l'interlocutore, ma non affronta del tutto l'essenza della prima e lo lascia sempre un po' perplesso. Noi abbiamo cercato di spiegarlo attraverso palloncini che si gonfiano e a un Universo che equivale a una superficie sferica e non a tutta la sfera, ma il dubbio, spesso, resta.

Oggi voglio darne una prova veramente elementare, legata a una geometria alla portata di chiunque. L'unica cosa necessaria è una minima conoscenza di cosa sia un sistema di riferimento, anche solo cartesiano.

Mettiamoci pure in un piano per non complicare le cose, anche se sarebbe, ovviamente, più realistico lavorare  in tre dimensioni. La seconda cosa di cui abbiamo bisogno è di un... superastronomo, che abbia a disposizione una tecnologia eccezionale. La sua risposta soddisferebbe in pieno la prima parte della domanda, eliminando qualsiasi dubbio e senza nemmeno dover parlare di luce o non luce capace di raggiungerci. Anzi, spiegherebbe anche un Universo capace di mettersi sempre in mostra, anche nelle sue prime fasi.

Semplifichiamo, perciò, il nostro Universo e rendiamolo simile a un incredibile numero di palline che decidono di allontanarsi una dall'altra, cercando, perciò, di occupare uno spazio sempre più grande o -meglio- di creare uno spazio sempre più grande

Tutte le palline unite insieme rappresentano la nascita del Big Bang. Potremmo dire che esse occupano un certo spazio, ma non lo possiamo dire, dato che lo spazio non è ancora nato. Questo fatto conferma da solo il problema riguardante le dimensioni e "forma" del Big Bang. Esso non può avere forma e dimensioni dato che lo spazio non esiste. Ma, ancora più importante, è la ricerca della sua posizione. Non può avere una posizione, dato che non esiste  ancora lo spazio e, quindi, non esiste un piano di riferimento in cui indicare le sue coordinate.

Possiamo, perciò, anche considerare l'insieme di tutte le palline come un punto geometrico, pur sapendo, che poco ha a che fare con un vero punto, dotato di certe dimensioni. La cosa più importante è che non esiste ancora un piano, ossia uno spazio, che possa servirci per stabilire la posizione di questo "strano" punto-non punto. Se esistesse un piano del genere vorrebbe dire che il Big Bang apparterrebbe a un certo spazio già esistente, ma questo andrebbe contro l'ipotesi fondamentale che prima di lui non esisteva lo spazio.

Chiamiamo perciò questo punto-non punto col nome di punto singolare, ossia di un qualcosa che ha dimensioni NULLE, dato che non esiste ancora lo spazio, e di una posizione del tutto sconosciuta, dato che non esiste ancora un sistema di riferimento. Scusate le ripetizioni, ma è necessario entrare perfettamente nelle modalità di ciò di cui stiamo parlando e dell'avventura "scientifica" che andiamo a raccontare.

N.B.: la singolarità di questo "qualcosa" può anche essere dimostrata fisicamente. La massa di tutte le palline non può cambiare, ma esse occupano uno spazio nullo, ossia un volume nullo. Ne segue che il punto singolare avrebbe una densità pari alla massa totale divisa per  zero, ossia la densità sarebbe infinita e cadremmo nuovamente in un assurdità o singolarità che dir si voglia (quanto assomiglia a un buco nero, vero...?)

Ad un certo istante le palline decidono di muoversi e di cercare di vivere in modo più o meno indipendente. Esse, quindi, creano uno spazio in cui misurare delle distanze. Per completezza dovremmo anche dire che non potremmo mai sapere QUANDO è nato l'Universo, dato che non esiste ancora una scala dei tempi su cui misurare l'attimo della nascita (anche il tempo nasce in quel momento). L'unica possibilità è quella  di misurare il tempo dopo il Big Bang, dando a quest'ultimo il valore di tempo uguale a ZERO.

Facciamo pure la Fig. 1, che rappresenta in modo molto schematico ciò che abbiamo detto, e che ci permette anche di rappresentare il Big Bang come un punto geometrico, pur sapendo che è solo una convenzione. Ce lo possiamo permettere anche perché un attimo dopo (ed essendo DOPO appartiene anche a uno spazio) le sue dimensioni sono già misurabili e sono incredibilmente piccole. Ciò ci dice anche che lo spazio, formato dalle palline in libera uscita, è uno spazio in espansione.

La figura mostra l'Universo in tempi diversi. Più il tempo è grande e più le palline occupano una circonferenza di raggio maggiore... chiamiamola pure "espansione".

Bene, ipotizziamo pure che il nostro superastronomo stia su una pallina (ad esempio O). Attraverso la tecnologia eccezionale di cui dispone, vorrebbe identificare la posizione del Big Bang. Accidenti, pensa e ripensa, alla fine si convince che può farlo in modo puramente osservativo. Lui sta vivendo nell'istante t = 3 e ha due grandi possibilità, offertegli dalla super tecnologia:

(1) in ogni istante riesce a vedere solo e soltanto la distribuzione delle palline in quell'istante. In altre parole NON è vincolato dalla lentezza della luce e quindi non è costretto a mischiare oggetti che occupano lo stesso spazio, ma che hanno inviato la loro luce in tempi diversi.

(2) E' capace di tornare indietro nel tempo, con moderazione, e vedere la distribuzione delle palline in tempi precedenti, ossia t = 2 e t = 1, ad esempio.

Beh, lui è molto ottimista, dato che possiede un suo sistema di riferimento e, quindi, può rappresentare la distribuzione delle palline al tempo t = 3, come mostra la Fig. 2.

Ha scelto due palline (A e B), ha determinato le loro coordinate e le ha inserite nel suo sistema di riferimento. Tutto molto facile... Adesso, non gli rimane che tornare indietro nel tempo (a  t = 2, ad esempio) e determinare nuovamente le coordinate delle palline A e B Facendo la differenza tra le coordinate di A e B in tempi diversi può facilmente scoprire qual è il loro movimento ed estrapolando all'indietro arrivare al loro punto d'incontro, ossia alla posizione del Big Bang.

La Fig. 3 mostra la nuova determinazione, fatta in t = 2, chiamando A' e B' le palline al tempo t = 2, con le loro coordinate x_A', y_A', x_B' e y_B'.

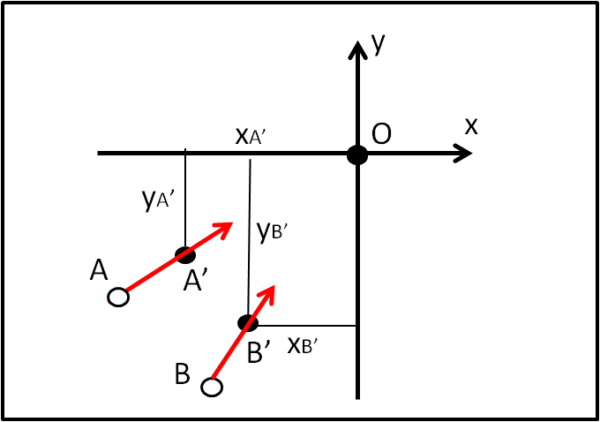
Facendo la differenza tra le coordinate x e y delle palline A e B in tempi diversi, risulta banale per O determinare il loro movimento e risalire sempre più indietro fino al punto iniziale. Ciò gli permette, in pratica, di identificare quel punto nel suo piano di riferimento. Ammette pure di non essere proprio in grado di arrivare fino a t = 0, dato che avrebbe a che fare con un punto molto speciale e dato che il suo sistema di riferimento cesserebbe di esistere, ma potrebbe sempre fermarsi quando ancora manca un po' di tempo (i salti troppo lunghi non gli sono  ancora permessi) rispetto a ZERO e avrebbe, perciò, una stima più che buona della posizione del centro delle palline, della loro origine, ossia del Big Bang.

In realtà, le palline A e B si sono mosse e sicuramente si sono avvicinate (A' e B') al punto di nascita. "Evviva, evviva", dice il superastronomo, "ho individuato la posizione del Big Bang". Però, però... quella posizione sembra un po' strana. Sembra, infatti, che le palline viaggino nel tempo proprio verso di lui.

Meglio che faccia ancora un salto indietro nel tempo, all'altroieri, t= 1, misurare nuovamente la posizione A" e B" al tempo t = 1 e inserirle nel suo sistema di riferimento. Detto fatto, come mostra la Fig. 4.

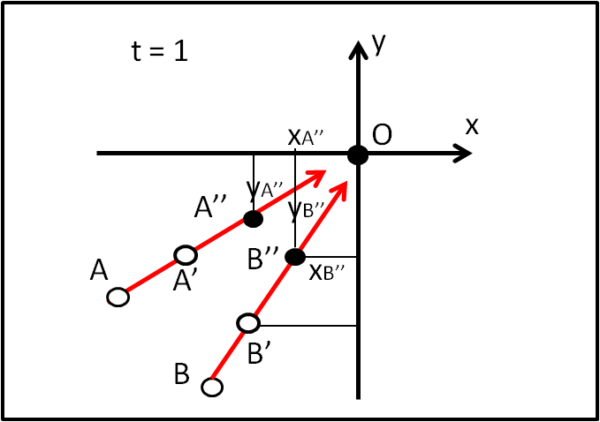
Il superastronomo non ha più alcun dubbio e conclude con un pizzico di orgoglio: "Le linee vengono verso di me. Sono io il centro dell'Universo, sono io nella posizione del Big Bang! E l'ho determinato solo attraverso le osservazioni".

Poi, però, ci riflette  sopra e capisce che il suo stesso identico ragionamento e disegno lo avrebbero fatto tutti i superastronomi delle varie palline, compresi, ovviamente quelli di A e di B. Anche loro direbbero che occupano la posizione del Big Bang. In altre parole, chiunque nell'Universo sarebbe giustamente convinto di essere nella posizione del Big Bang. Ne segue che dovunque uno guardi può vedere la posizione del Big Bang. Il Big Bang è OVUNQUE!

Il succo del discorso è sempre lo stesso... Il sistema di riferimento di O si muove con lui, dato che non esiste pallina privilegiata. Ciascuna pallina rappresenta il Big Bang in tempi successivi al tempo t = 0. Se arrivassimo a un tempo infinitamente vicino a t = 0, tutti i sistemi di riferimento delle palline tenderebbero a coincidere. Dove? Non si può assolutamente rispondere, perché al tempo t = o non esisterebbe più nessun sistema di riferimento. Resta, però, il fatto che, in tempi successivi, ogni origine dei sistemi di riferimento delle palline rappresenta la posizione del Big Bang. Insomma, non c'è niente da fare, il Big Bang si vede dappertutto.

Spero di avere aiutato e non di avere confuso di più le idee...

 

Per approfondire l'argomento, consigliamo la lettura dei primi capitoli di "Dante-Riemann-Einstein: Dio e il Big Bang" (in particolare il capitolo 3A - figura 19 e seguenti)