Risolto (da Leandro) il problema della costruzione della tangente all'ellisse in un punto, possiamo cominciare a giocare a biliardo su un tavolo dalla forma molto particolare: l'ellisse.

Tracciamo la retta che congiunge il punto qualsiasi P dell'ellisse con il fuoco F1 e prolunghiamola di un segmento PF2'uguale a PF2. Si dimostra subito che la traiettoria da F1 a P e poi a F2 è quella di minima distanza (ossia quella che deve percorrere la pallina). Infatti, F1PF2' è sicuramente la minima distanza tra F1 e F2', ma, dato che PF2' e uguale a PF2 risulta che anche F1PF2 è la traiettoria di minima distanza NON DIRETTA (ossia dopo un rimbalzo) tra i due fuochi. Ne segue che ogni traiettoria che da F1 va a un punto P qualsiasi deve proseguire, dopo il rimbalzo, verso F2. Questo fatto è quello fondamentale per giocare a biliardo. Non ci resta quindi che lanciare la pallina verso P e concludere che essa deve rimbalzare e passare anche per F2. I

n questo caso, molto utile, non ci sarebbe assolutamente bisogno di tracciare la tangente all'ellisse per sapere come tracciare la linea dopo il rimbalzo. Tuttavia, a noi interessa anche saper disegnare le traiettorie della pallina quando non passa per uno dei fuochi. Questo caso generale abbisogna della conoscenza della tangente per poter disegnare la traiettoria dopo il rimbalzo, tenendo conto della legge della riflessione (la stessa relativa a un raggio di luce). Basta, infatti, tracciare una linea che formi con la tangente un angolo uguale a quello di arrivo in P. Bene, utilizziamo la Fig. 1.

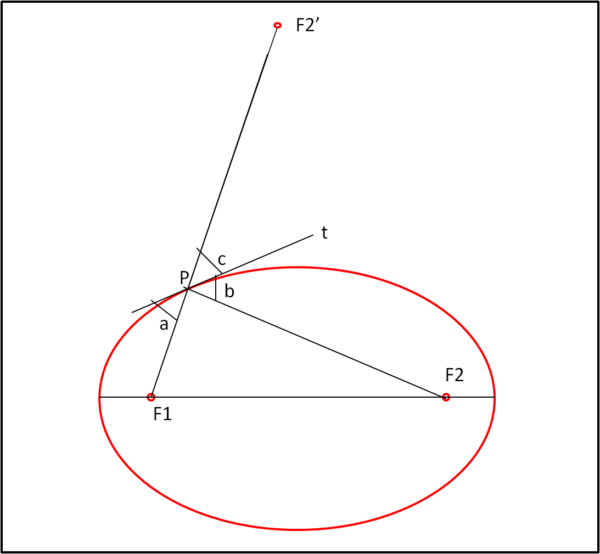
Basta tracciare la bisettrice tra la semiretta PF2' e PF2. Essa è proprio la tangente t all'ellisse nel punto P. Infatti, l'angolo a è uguale all'angolo c perché angoli al vertice. Ma b deve essere uguale ad a per la legge di riflessione e, di conseguenza, l'angolo b deve essere uguale a c. La bisettrice t è quindi la tangente richiesta.

Bene, ora sappiamo come disegnarla facilmente e cominciamo con la nostra prima partita. Il nostro avversario conosce poco la geometria, per cui potremmo facilmente scommettere con lui che se ponesse la sua pallina sul punto F2 (non diciamogli certo che cosa è il fuoco) noi potremmo lanciare la nostra anche a occhi chiusi, in qualsiasi direzione, ma colpiremmo sempre, dopo un rimbalzo, la sua pallina. Ovviamente, noi possiamo mettere la nostra pallina in qualsiasi punto del tavolo da gioco e basterà che il nostro tiro passi per il punto F1.

Non solo, ma potremmo anche stupirlo dicendo  che se leva la sua pallina qualsiasi nostro tiro finirebbe presto o tardi per percorrere la traiettoria diretta che passa da F1 e F2, ossia, per noi che "sappiamo" l'asse maggiore dell'ellisse. Provare per credere, come mostra la Fig. 2

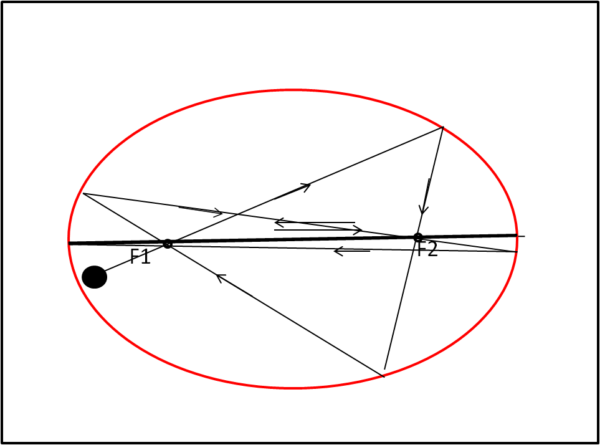
Tutto ciò, ovviamente, se il tavolo è perfetto come il nostro tiro e se la pallina viene considerata puntiforme! Sembra una sciocchezza, ma sono convinto che qualcuno resterebbe stupito...

Ma andiamo oltre con le nostre scommesse. Questa volta facciamo tirare lui e noi mettiamo la nostra pallina tra la sponda e il fuoco F1. Poi sfidiamo il nostro avversario a colpirla con il numero di sponde che vuole, dicendogli però che il suo tiro deve passare tra F1 e F2. Ammettendo che  la pallina non rallenti il suo moto, potremmo tranquillamente andarcene e tornare dopo ore e ore, ma la sua pallina non riuscirà mai a colpire la nostra, qualsiasi angolazione le dia. Quello che succederà è una cosa molto sorprendente. Tutte le traiettorie della pallina, per un numero molto alto di ribalzi, disegneranno ciò che si vede in Fig. 3, ossia saranno compresi all' interno di un'iperbole che ha per fuochi ancora F1 e F2.

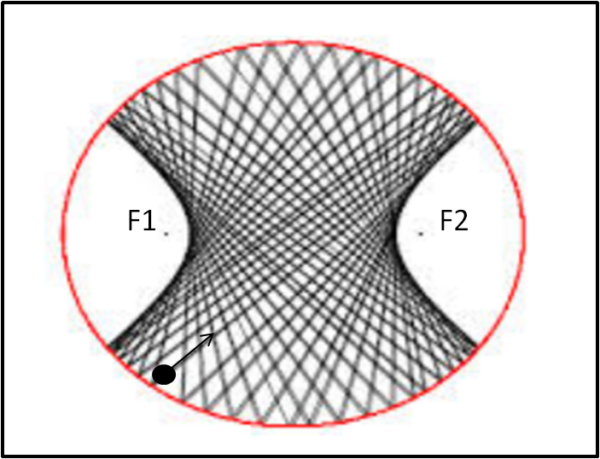
Vogliamo esagerare? Bene, ora mettiamo la nostra palina in un qualsiasi punto che stia sulla congiungente i due fuochi F1 e F2. Questa volta sfidiamo il nostro avversario a colpirla, facendo però il primo tiro in modo che la traiettoria passi tra la sponda e uno dei due fuochi. La sfida ci vedrà sempre vincitori, dato che la pallina compirà sempre tragitti tali da risultare tangenti ad un'ellisse più piccola di quella iniziale, ma con gli stessi fuochi, come mostra la Fig. 4.

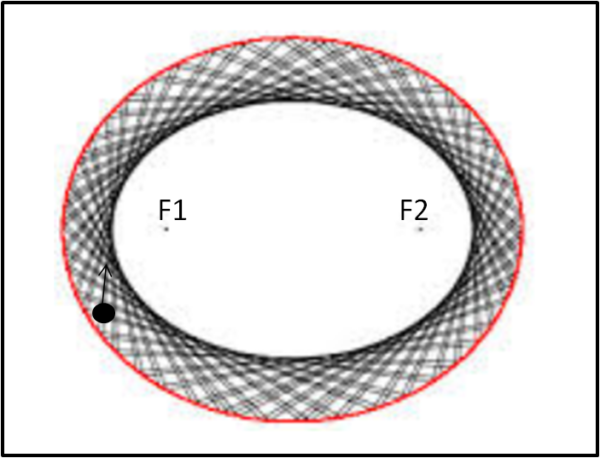
In entrambi i casi la forma e le dimensioni dell'iperbole o dell'ellisse dipenderanno dall'angolazione del tiro rispetto all'asse maggiore.

Vi è però un'altra possibilità, ossia quella di effettuare un tiro tale da ripassare per lo stesso punto iniziale. L'andamento sarebbe periodico (Fig. 5) e l'insieme delle linee formerebbero un poligono di almeno tre lati.

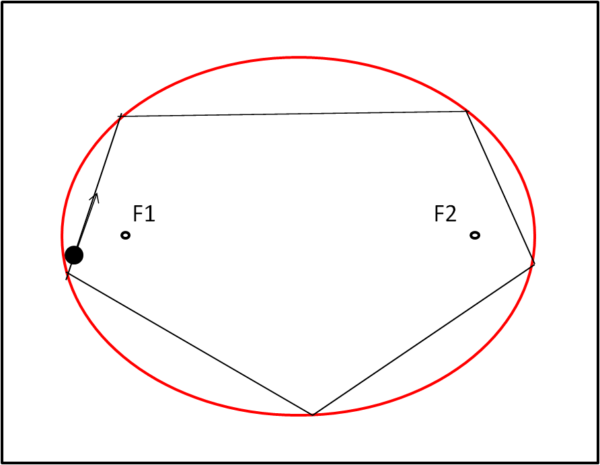
Ma su questo caso torneremo una prossima volta. Terminiamo col dire che il tutto si semplifica senza perdere di interesse se l'ellisse si trasforma in un cerchio. I fuochi coincidono nel centro e qualsiasi tiro si faccia, che non passi per il centro non vi passerà mai, ma identificherà un cerchio di raggio minore. Se, invece il tiro passa per il centro farà sempre lo stesso ad ogni rimbalzo. Provate pure anche perché la tangente è sempre perpendicolare al raggio ed è di facilissima costruzione.

Su, che aspettate, costruitevi un biliardo circolare o ellittico!