Categorie: Matematica Riflessioni
Tags: dispari divisori fattori pari quadrati perfetti quiz soluzione
Scritto da: Vincenzo Zappalà
Commenti:2
Solo i quadrati restano aperti ***
Il problema è piuttosto interessante e, come sempre, Fabrizio non ha perdonato. Voglio, comunque, cercare di spigare la strategia da usare per ottenere il risultato nel modo più rapido, in modo estremamente didattico, anche se, probabilmente, addirittura pedante. Il quiz deve avere spaventato... ma non è poi così difficile.
Cominciamo con guardare cosa capita alle prime 5 porte.
Porta 1: essa viene modificata SOLO al primo passaggio, dato che dopo viene sempre trascurata. Rimane perciò APERTA
Porta 2: essa viene modificata al primo e al secondo passaggio. Aperta - Chiusa = CHIUSA
Porta 3: essa viene modificata al primo e al terzo passaggio. Aperta - Chiusa = CHIUSA
Porta 4: essa viene modificata al primo, al secondo e al quarto passaggio. Aperta - Chiusa - Aperta = APERTA
Porta 5: essa viene modificata al primo e al quinto passaggio. Aperta - Chiusa = CHIUSA
Accidenti, sembrerebbe che il fatto di rimanere aperta o chiusa sia del tutto casuale... Ma, analizziamo bene la situazione.
La porta 1 subisce solo un passaggio, la 4 tre passaggi. In altre parole la porta 1 e la porta 4 subiscono un numero DISPARI di passaggi.
La porta 2, la porta 3 e la porta 5 subiscono , invece, un numero PARI di passaggi. Anche se con pochi esempi ci stiamo facendo l'idea che la porta resti chiusa quando il numero di passaggi è PARI e resti aperta quando il numero di passaggi è DISPARI. Proviamo con due numeri qualsiasi...
Prendiamo il numero 50. Quali saranno i passaggi che lo interessano. Sicurante il primo e il cinquantesimo; ma, anche il secondo, il quinto, il decimo e il venticinquesimo. In conclusione il 50 subisce 6 passaggi, che è numero pari, e, quindi, la porta resterà CHIUSA. Sembra proprio confermata la nostra ipotesi.
Prendiamo, adesso il numero 23. Il 23 è un numero primo, per cui la porta 23 verrà modificata solo due volte, ossia la prima e la ventitreesima. Ancora una volta un numero pari di passaggi e quindi deve restare CHIUSA.
Direi che è il momento di essere meno empirici e capire quali sono i passaggi che cambiano la posizione della porta. E' immediato pensare ai suoi DIVISORI (o se preferite FATTORI). Attenzione: non fattori primi, ma solo fattori, ossia numeri tali che la divisione del numero della porta considerata (ad esempio la 50) per questi numeri dia un risultato esatto, con resto zero. Riprendiamo il 50. Quali sono i suoi fattori? Presto detto: 1, 2, 5, 10, 25, 50. Infatti,
50 : 1 = 50
50 : 2 = 25
50 : 5 = 10
50 : 10 = 5
50: 25 = 2
50 : 50 = 1
In altre parole sembrerebbe sufficiente contare i fattori e concludere che se essi sono in numero pari la porta resterà chiusa, mente se essi sono in numero dispari la porta resterà aperta.
Controlliamo, ancora una volta per un numero che abbia un numero dispari di fattori. Ad esempio 49.
I suoi divisori sono 1, 7, 49 = aperta-chiusa-aperta = APERTA.
Perfetto! La nostra conclusione è esatta. Non ci rimane, quindi che contare i divisori del nostro numero... Siamo, però, sicuri che sia la strategia più semplice? No, assolutamente no.
Cambiamo leggermente la scrittura relativa al numero 50:
50 = 1 x 50
50 = 2 x 25
50 = 5 x 10
50 = 10 x 5
50 = 25 x 2
50 = 50 x 1
I prodotti tra divisori, appena svolti, danno sempre il valore finale di 50. Cosa succede, invece al 49?
1 x 49 = 49
...
49 x 1 = 49
Non abbiamo, però, considerato il divisore 7. Anche lui, in qualche modo deve dare il risultato di 49. L'unico modo per ottenere ciò è moltiplicare 7 per se stesso:
1 x 49 = 49
7 x 7 = 49
49 x 1 = 49
Cosa succede ai numeri che hanno un numero dispari di divisori? Presto detto: essi devono assolutamente essere dei quadrati perfetti, in modo da accettare la moltiplicazione di un divisore per se stesso.
Conclusione? Non c'è assolutamente bisogno di scrivere i divisori e contarli, ma basta scrivere i numeri che sono quadrati perfetti: Essi sono quelli delle porte che restano aperte! In altre parole, i numeri che possiedono un numero DISPARI di divisori DEVONO essere dei quadrati perfetti. Ed ecco, quindi, il risultato finale...
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 sono le uniche porte che restano aperte dopo 100 passaggi.
P.S.: Abbiamo notato che la matematica da applicare è quella più elementare possibile. La vera difficoltà sta solo nel RAGIONAMENTO.
2 commenti
Propongo un metodo che mi sembra in parte alternativo a quello descritto sopra.
Parto dal fatto che solo le porte delle stanze che hanno un numero che ha un numero di divisori dispari rimangono aperte per le regioni spiegate sopra.
Il numero di divisori può essere calcolato a partire dalla scomposizione in fattori primi.
Ad esempio il numero 30 è scomponibile in 2x3x5. I divisori saranno 1 2 3 5 2x3 2x5 3x5 2x3x5.
Il modo più veloce per arrivare al numero di divisori senza contarli uno ad uno mi sembra questo. Immagino di mettere in un contenitore ciascuno dei tre divisori insieme ad 1: (1,2) (1,3)(1,5). Poi prendo un numero da ciascun contenitore in tutti i modi possibili ottengo tutti i divisori: 1x1x1, 2x1x1,1x3x1,....,1x3x5,2x3x5 (quindi l'1 nel contenitore rappresenta i casi nei quali quel numero primo non fa parte del divisore). In questo modo è facile calcolare quanti sono i divisori. In questo caso è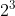
, posso scegliere il primo numero in 2 modi diversi e così anche il secondo ed il terzo. Lo stesso metodo vale qualsiasi sia il numero di fattori primi. Se i fattori primi sono n il numero di divisori sarà 
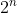. Che è sempre un numero pari, quindi porta chiusa.
Nel caso uno o più fattori non siano proprio un numero primo, ma una sua potenza, devo considerare nel contenitore anche le potenze del numero primo. Ad esempio, per 12 che è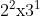
ci saranno due contenitori che contengono \;&space;(1,3))
. Il numero di elementi in ciascun contenitore è dato dalla potenza del numero primo + 1. Il numero di divisori di 12 è quindi (2+1)x(1+1)=6, ancora un numero pari, porta chiusa.
Ora il caso generale. Prendo un numero N che ha come fattori primi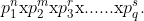
Il numero di divisori di N sarà dato dal prodotto (n+1)(m+1)(r+1)...(s+1).
In un prodotto basta che ci sia un moltiplicatore pari che il risultato è pari.
Per essere dispari (porta aperta) devono essere tutti dispari. Questo significa che m, n, r ecc. devono essere tutti pari. Ad esempio 36 che è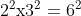
. Quindi le porte aperte hanno un numero N quadrato di un intero: 
.
ovviamente va bene... l'importante direi è capire che le porte aperte devono essere quadrati perfetti. Trovare i divisori dei numeri da 1 a 100 è cosa estremamente facile, ma non ce n'è bisogno, dato che basta controllare se il numero è un quadrato oppure no.