Questo articolo è stato inserito nella pagina d'archivio "Dinamica e Meccanica", in Fisica Classica.

(Chi è digiuno delle basi della dinamica, trova QUI le informazioni propedeutiche alla comprensione di questo articolo)

 

Potevamo non ricavare l'equazione del razzo (molto semplificata), dopo avere parlato di SpinLaunch? In realtà lo avevamo già fatto QUI, ma questa volta affrontiamo l'argomento in modo più approfondito, oltre che semplificato (nell'appendice finale).

Premetto che io non sono un ingegnere spaziale, per cui la mia trattazione sarà estremamente semplificata e legata soltanto alla fisica classica. In poche parole, terrò in conto solo la conservazione della quantità di moto in uno spazio vuoto, trascurando la gravità.

Molti anni fa parlavo delle missioni spaziali con un tizio digiuno completamente della fisica di base.  Con lui parlare di conservazione della quantità di moto era come parlare arabo. In tali casi, la logica e la razionalità imporrebbe uno studio preparatorio anche se di livello estremamente basso. Tuttavia, anche a quei tempi regnava una specie di rifiuto della Scienza. Innanzitutto, perché studiarla, anche se superficialmente imponeva una fatica mentale, seppur piccola. E questo era un onere troppo grande. Una cosa è faticare fisicamente anche al di là dei propri limiti e un'altra cosa è mettere in moto il proprio cervello. Purtroppo le cose non sono migliorate, anzi... Oggi non solo non si vuole ragionare, ma si cercano anche soluzioni alternative, legate ad atti di fede, che impegnano poco e istigano alla rabbia e alla demolizione di tutto ciò che richiederebbe l'uso del povero cervello, bisognoso di non affaticarsi più di tanto.

Il caso che veniva sollevato era: "Come fanno i razzi ad acquistare velocità?". Niente da fare, il conoscente diceva che per lanciarsi in avanti ci vuole un punto d'appoggio su cui esercitare una forza. Nello spazio? Beh... c'è della polvere e la cosa non cambia. Dire che si può guadagnare velocità anche nel vuoto, proprio grazie alla conservazione della quantità di moto era impresa impossibile. Mi guardava come si guarda un povero mentecatto credulone. No, senza spinta contro qualcosa non si può viaggiare. Punto e a capo. Eh sì, la Scienza dice un sacco di bugie, che la pratica di tutti i giorni smentisce. Mi ricordo un esempio perfetto che ha usato per dimostrarmi il mio errore: "Prova a lanciare una pietra lontano da te... non dirmi che ti muovi in senso contrario". Insomma, anche la forza di gravità restava un piccolo mistero o, forse, un'invenzione, frutto di "sfaticati"  che dicevano di  lavorare a tavolino piuttosto che faticare fisicamente.

Forse la migliore definizione di "scienziato" me l'ha data circa 30 anni fa un contadino che lavorava in una vigna vicina a casa mia. Molto curioso dei "nuovi arrivati" in paese, mi chiese espressamente che lavoro facevo. Dopo un certo tempo passato a spiegargli che una cosa sono gli astronomi e un'altra sono gli astrologi, ho cercato invano di descrivergli il lavoro di ricerca e le sue conseguenze anche molto pratiche. Mi guardava con aria molto dubbiosa e alla fine mi ha detto, non sorridendo, ma seriamente: "Ah, ho capito... lei è uno di quelli che prende un mucchio di soldi per non fare niente!". Insomma, alla pari di un burocrate tipo che, almeno, cerca di inventarsi qualcosa pur di apparire sovraccarico di lavoro.

Va bene, archiviata una serata con un po' di nervosismo e tanta pena, oggi ci ritroviamo in condizioni ben peggiori. C'è niente da fare, il cervello è un organo che non deve faticare, al limite credere in qualcosa e poco importa che sia una specie di magia, l'importante è riuscire a capirla. Sapete che il numero di coloro che credono che sia il Sole a girare attorno alla Terra sta aumentando? Come si può, infatti, negare l'evidenza: "Se guardo in cielo e prendo un albero come riferimento, è sicuramente il Sole che si sposta!" E chi non ci crede è sicuramente pagato da qualcuno e -forse- meriterebbe di fare la fine di Giordano Bruno.

Per essere giusti, devo dire che molti scienziati fanno ben poco per cambiare la situazione. Preferiscono parlare "difficile" e sperare che i paroloni incantino l'ascoltatore anche se non hanno le basi per capire. In varie occasioni, c'era sempre qualcuno, che si considerava istruito, che alla fine di una mia conferenza divulgativa, mi diceva: "Sì, bravo, bravo, ma... troppo semplice!" Beh, io ho sempre preferito quel tipo di commento che sentirsi dire: "Lei deve avere un cervello eccezionale... ma io non ho capito assolutamente niente!". La stessa persona, però, non avrebbe più partecipato a conferenze divulgative e avrebbe piano piano trasformato l'ignoranza in rabbia verso quei fanfaroni incomprensibili.

Fatte queste premesse, vediamo di affrontare la cosiddetta equazione del razzo, formulata dal russo Tsiolkovsky nel 1903, anche se già nel 1813 il matematico inglese Moore aveva derivato qualcosa di molto simile.

Il significato è oltremodo semplice per chi conosce un po' di fisica, ma merita sempre di essere divulgata con la massima chiarezza.

Siamo di fronte a una "costruzione" che deve volare e che quindi deve anche avere una forma aerodinamica. Al momento, però, supponiamo che l'atmosfera non esista. All'interno di questo "involucro" mettiamo parecchio materiale che verrà lanciato con una certa velocità nello spazio sotto forma di gas. Mettiamoci anche in un sistema di riferimento esterno, ad esempio un osservatore terrestre. Ebbene, il concetto fondamentale è che il razzo, compreso il suo "carburante" da lanciare, costituisce un solo sistema. Tale sistema, se non subisce forze esterne (escludiamo la gravità), deve conservare la sua quantità di moto, qualsiasi cosa avvenga al suo interno. Questa è una legge fisica confermata in tutti i modi possibili.

Diciamolo in altre parole, del tutto analoghe. La variazione della quantità di moto è una forza, ossia è una massa moltiplicata per la variazione di velocità, ossia per l'accelerazione.  Se ho un sistema isolato posso quindi agire dal di fuori impartendogli una certa forza F. In tal modo varierei la quantità di moto del sistema. Ma se agisco all'interno del sistema applicando solo a una parte di esso una forza F, il terzo principio della dinamica mi dice che a questa forza deve corrispondere una forza uguale e contraria che agisce sulla parte restante. Le forze in gioco sono uguale e contrarie e quindi non esiste forza esterna. Ciò comporta la costanza della quantità di moto.

Ho fatto questa precisazione, dato che a volte si legge che l'equazione che vogliamo determinare si ottiene dalla terza legge della dinamica e, a volte, dalla legge della conservazione della quantità di moto. In realtà, come appena detto, le due trattazioni sono del tutto equivalenti.

Abbiamo già visto molti fenomeni in cui la conservazione della quantità di moto ha un ruolo essenziale. L'importante è avere a disposizione un sistema isolato. Questo sistema può essere composto all'inizio da due masse separate che vengono a contatto e siamo nel caso dell'urto elastico, ad esempio. Ma, può essere composto da una sola massa iniziale che viene poi separata in due: questo è il caso, ad esempio, dello sparo con un fucile e del fenomeno del rinculo. In un caso abbiamo un urto tra due masse, nell'altro la separazione di due masse. Poco importa, però, dato che in entrambi i casi le forze che agiscono sono INTERNE al sistema e quindi non comportano variazione della quantità di moto del sistema.

Il caso del razzo è molto simile a quello del rinculo, con qualche piccola variante. Mentre lo sparo è uno e uno solo, e così in rinculo, il razzo continua a espellere massa e quindi il fenomeno si propaga nel tempo e quindi la massa del razzo continua a diminuire a favore del combustibile espulso.

Supponiamo che, ad un certo istante t, la massa del razzo (compreso il combustibile) valga m e che la sua velocità rispetto a un osservatore terrestre sia v_RT. All'istante t ' = t + dt, dopo che è stata bruciata una frazione di combustibile ed è stata espulsa, la massa del razzo sarà m' = m – dm e la corrispondente velocità v_RT' = v_RT + dv_RT.
La velocità del gas, rispetto al razzo(velocità di scarico) sia v_GR, costante ed opposta a quella del razzo rispetto al gas. La velocità del gas rispetto a terra, all'istante t', indicata con v_GT , è:

v_GT = v_GR + v_RT

non dimenticando, infatti, che il gas ha, comunque, la velocità del razzo (primo principio della dinamica) cui va aggiunta vettorialmente quella del gas rispetto al razzo e, soprattutto, che si conserva la quantità di moto e non la somma delle velocità (vedi appendice facilitata).

La quantità di moto totale del sistema (razzo + gas) all'istante t vale:

q = m v_RT

mentre all'istante t' vale:

q' = (m – dm) v_RT' + dm v_GT = (m – dm) v_RT' + dm (v_GR + v_RT)

Poiché il razzo e il gas formano un sistema isolato, si può applicare la conservazione della quantità di moto (q = q'):

m v_RT = (m – dm) (v_RT + dv_RT) + dm (v_GR + v_RT)

m v_RT = m v_RT - dmv_RT + mdv_RT - dmdv_RT + dm v_GR + dm v_RT

m dv_RT = – dm v_GR

dopo aver semplificato ed avere trascurato il termine dm dv_RT in quanto contiene un prodotto di due infinitesimi.

Dividiamo entrambi i termini per dt

m dv_RT/dt = – v_GR dm/dt              .... (1)

Il primo termine non è altro che una forza, ossia la forza che viene trasmessa al razzo, chiamata forza di propulsione F_PR

F_PR = - v_GR R

Dove R è la rapidità con cui viene espulso il gas.

Ne segue che il razzo riceve una "spinta" che è proporzionale sia alla velocità di espulsione del gas (sempre costante) che alla rapidità di consumo del carburante (ossia alla rapidità con cui cambia massa).

Per aumentare la spinta  il metodo migliore è quello di aumentare v_GR perché l'aumento di R comporta un aumento del consumo di combustibile nell'unità di tempo e pertanto un corrispondente aumento della massa iniziale senza un equivalente aumento di accelerazione.
L'aumento di v_GR si ottiene sia intervenendo sulle caratteristiche dell'ugello da cui vengono fatti fluire i gas di combustione, sia aumentando la loro temperatura e, su questo fronte, l'unica limitazione è costituita dalle
caratteristiche di resistenza dei materiali utilizzati.

N.B.:  La (1) è un'equazione differenziale in cui compaiono la derivata di v_RT e di m rispetto al tempo. Ricordando che v_GR è una costante, si può effettuare l'integrale, tra un tempo iniziale e uno finale, per determinare la variazione della velocità del razzo in relazione alla variazione di massa, dovuta all'espulsione del combustibile. L'equazione, quindi, viene anche descritta come:

Δv_RT = v_GR ln (m_I/m_F)

Infatti: 

∫_tI^t_F(dv_RT/dt) dt= – v_GR ∫_tI^t_F((dm/m)/dt) dt

∫_vI ^v_F dv_RT= – v_GR ∫_mI^m_F (1/m) dm

Δv_RT = - v_GR ln (m_F/m_I) = v_GR ln (m_I/m_F)

dove m_I è la massa iniziale del razzo (con il combustibile ancora al suo interno) e m_F la massa finale del razzo senza più combustibile.

Al decrescere della massa del razzo si continua ad aumentare la sua velocità del razzo. Non per niente, vengono sganciati i serbatoi ormai vuoti.

Appendice facilitata *

Questa breve appendice potrebbe essere inutile, ma niente vieta di fare un esempio molto qualitativo per evitare eventuali confusioni... Immaginiamo di avere due palline di massa diversa che siano ferme e a contatto una con l'altra. La quantità di moto del sistema è uguale a zero.

Per un qualsiasi motivo "interno" (la bacchetta magica di una fata) le due palline iniziano ad allontanarsi tra loro. Devono avere velocità uguali e contrarie? Assolutamente no, devono, invece, avere delle quantità di moto uguali e contrarie. Se una pallina ha una massa m superiore alla massa m' dell'altra, deve andare a velocità v minore di v' dato che ciò che deve conservarsi è la somma delle quantità di moto, che deve sempre restare la stessa, ossia uguale a zero:

(m + m') · 0 = 0             istante t = 0, v = 0

m v + m' v'  = 0                 istante t = 1, v < v'

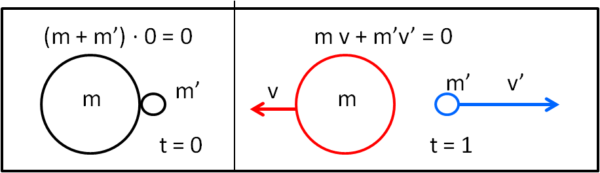
Nel caso del razzo la faccenda si complica, dato che la pallina più grande diminuisce continuamente la sua massa, mentre continuano a partire in verso contrario tante palline di massa uguale m'.  Possiamo raffigurare il tutto con una massa m a cui sono attaccate due (o quante volete) palline di massa m'. Ovviamente, la pallina di massa m è il razzo, mentre le palline di massa m' sono il propellente.

Al tempo t = o tutto è fermo e la quantità di moto è uguale a zero. Al tempo t = 1, si stacca una pallina di massa m': verso sinistra viaggiano, a velocità v1, la pallina di massa m e una di massa m', che le sta attaccata, verso destra una sola pallina di massa m'. Al tempo t = 2, si stacca anche l'altra pallina di massa m'. Ne segue che la pallina di sinistra rimane da sola, con la sua massa m, mentre a destra abbiamo due palline di massa m' che viaggiano isolate e che si portano via, ciascuna, la stessa quantità di moto. Ad ogni istante la quantità di moto totale deve conservarsi, per cui v2 > v1 e continuerà a crescere ogni volta che si stacca una pallina di massa m' (ogni volta che viene espulso del gas).

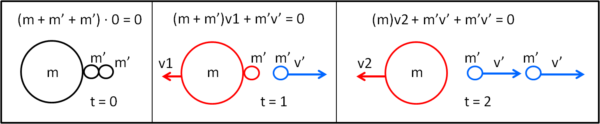
Ovviamente la pallina di massa m è l'involucro del razzo, mentre la somma delle palline di massa m' è il combustibile che viene espulso a "blocchi" di massa m'.

P.S.: In realtà, benché ciò che quel tizio intendeva dire era cosa ben diversa, il razzo, per accelerare, deve effettivamente spingere su qualcosa, ossia sul suo gas di scarico... Una faccenda che resta, però, in famiglia, dato che se considerassimo anche il gas espulso non vi sarebbe alcun cambiamento nella quantità di moto...