Questo articolo è stato inserito nella sezione d'archivio "Sezione Aurea, spirale di Fibonacci e altre forme ricorrenti nell'Universo"

 

Ancora sulla sezione aurea, ma mettendo in luce un'altra piccola dimenticanza di Euclide & Co.

La parte tra parentesi del titolo sembrerebbe richiamare i soliti antichi, greci soprattutto. In realtà, essi riuscirono molto bene a ottenere graficamente, con le loro sacre regole, il rapporto voluto e ancora oggi si dà come "ufficiale" la loro costruzione. Richiamiamola brevemente...

Dato un segmento di lunghezza a qualsiasi si costruisca il quadrato ABCD di lato a. Si determini il punto medio M del lato AB e da esso si tracci la congiungente tra lui e uno spigolo del quadrato posto sul lato opposto (ad esempio C). Con centro in M e raggio MC si tracci la circonferenza fino a incontrare il prolungamento di AB in E. Il rettangolo AEFD è un rettangolo aureo. Il rapporto tra i suoi lati AE e EF si chiama rapporto aureo e viene indicato con φ.

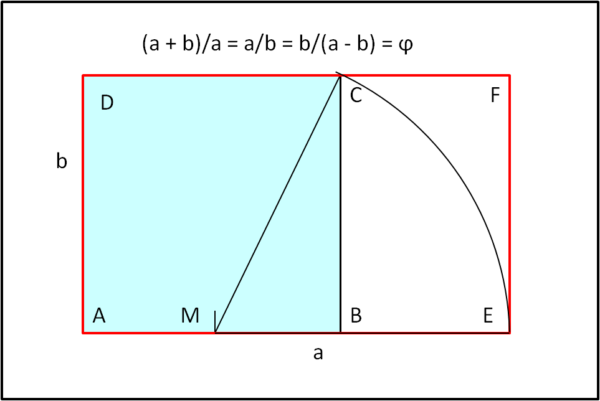
L'importanza per l'architettura è stata enorme, dato che se, escludiamo il quadrato di lato a, ciò che resta è ancora un rettangolo aureo e via dicendo scendendo sempre in dimensioni. Seguire questa regola porta a una perfetta armonia e il Partenone ne è un esempio perfetto, ma le opere d'arte basate su di essa sono praticamente infinite.

Oltre all'interesse artistico, il rapporto aureo ha avuto sempre un grande interesse matematico e la serie di Fibonacci ne è un esempio entusiasmante. Su questo argomento, però, la nostra Valentina ha scritto un lungo e accurato articolo.

Oggi, vogliamo solo dimostrare che, sebbene i greci non se ne fossero accorti (!), esistono altri metodi grafici che permettono di costruire il rapporto aureo. Uno, in particolare, è molto rapido e stupisce veramente che sia "scappato" ai grandi scienziati dell'antichità. Si basa su un triangolo equilatero e sul cerchio a lui circoscritto. Un interesse particolare è poi rappresentato da colui che l'ha proposto: un artista americano, tale George Phillips Odom Jr, amante della geometria che, dopo un tentato suicidio, fu internato in una ospedale psichiatrico. Un amico venne a sapere del metodo da lui ideato per costruire il rapporto aureo e lo pubblicò nel 1983.

Disegniamo un triangolo equilatero ABC, cosa che anche i greci erano in grado di fare, così come tracciare il cerchio circoscritto al triangolo. Disegniamo la retta passante per i punti medi M e N di due lati del triangolo fino a incontrare la circonferenza in H. Bene. Il rapporto tra MN e NH è proprio il rapporto aureo. Basta, allora, tracciare la perpendicolare a MN passante per N e determinare il punto P su di lei, intersezione con la circonferenza di centro N e raggio NH. Ne segue il rettangolo aureo MNPR.

In altre parole:

MN/NP = MN/NH = φ

Banale e rapido... Probabilmente Euclide si sta mordendo le mai!

Non ci resta che dimostrare quanto detto  a parole.

Ridisegniamo il nostro triangolo...

Tracciamo i segmenti CH e HB. Consideriamo i triangoli CHN e KNB. Essi sono simili avendo gli angoli uguali. Quello in H è uguale a quello in B, dato che sono angoli alla circonferenza sottesi dallo stesso arco KC. Quello in C e quello in K per la stessa ragione e relativamente all'arco BH (anche i due in N sono uguali perché opposti al vertice). Ne segue allora che:

KN/CN = NB/NH

KN, però, è uguale alla somma di KM e MN.

(KM + MN)/CN = NB/NH

Ma, per costruzione KM = NH

(NH + MN)/CN = NB/NH

Tuttavia CN = MN, dato che i triangoli CMN e ABC sono simili e, di conseguenza, anche CMN è equilatero. Possiamo scrivere:

(NH + MN)/MN = NB/NH

Ma, per quanto detto prima riguardo ai triangoli CMN e ABC, ricaviamo che NB = MN. Perciò:

(NH + MN)/MN = MN/NH

NH/MN + MN/MN = MN/NH

NH/MN + 1 = MN/NH

chiamiamo  MN/NH = x

Possiamo scrivere:

1/x + 1 = x

x  -1/x - 1 = 0

x²  - x - 1 = 0

Ma questa è proprio l'equazione di secondo grado che ha come soluzione la sezione aurea (vedi QUI), per cui possiamo scrivere:

x = MN/NH  = (1 + √5)/2 = φ

Ah, questi greci... un po' distratti!