Non prendetevela con me se torno ancora una volta a parlare di questa tecnica, tanto cara agli antichi greci. La "colpa" è del nostro amico Frank che mi ha pungolato varie volte nei commenti in questo recente articolo. Nelle mie risposta ve n'è una che merita un approfondimento ed è quella relativa a un poligono regolare di n lati qualsiasi.

Io ho detto che è sempre possibile costruirlo con riga e compasso, ma, in realtà, ciò è vero solo in modo approssimato.

Prima di iniziare puntualizziamo un  risultato fondamentale:

La costruzione è possibile solo per alcuni poligoni. Chi lo dice è un giovane scienziato che con i numeri ci sapeva fare benissimo: Gauss. Egli nel 1796 dimostrò che un poligono regolare di n lati è costruibile se la sua scomposizione in fattori primi è del tipo:

n = 2^k p₁ p₂ .... p_s

dove k è un numero intero non negativo e i fattori p_i sono numeri di Fermat primi

No, non abbiate paura... eviteremo, per adesso almeno, di parlare dei numeri primi di Fermat e ci limiteremo al fatto che NON tutti i poligoni di n lati qualsiasi sono realmente costruibili: se lo dice Gauss ci si può credere fermamente!

Tuttavia, come dicevo prima, si riesce, comunque, a farne una costruzione piuttosto realistica, anche se il procedimento porta a un poligono abbastanza approssimato. Questa precisazione, però, non sempre viene indicata... Noi vedremo di localizzare il "baco".

Prima di descrivere un paio di costruzioni, dobbiamo però ricordare ciò che è possibile fare con riga e compasso NON GRADUATI. Ormai conosciamo bene queste possibilità e ci basta ribadire che la costruzione di una perpendicolare e di una parallela a una retta data sono risultati ottenibili. Ricordiamo anche, però, che non è possibile usare il compasso come riga graduata, ossia non è possibile misurare con esso una certa distanza e poi, lasciandolo aperto, riportare questa distanza in un altra posizione: il compasso può solo fare centro in un punto e aprirsi fino a incontrare un altro punto già determinato.

A questo punto, allora, pongo una domanda estremamente semplice, ma che potrebbe non apparire così ovvia.

Dato un segmento di lunghezza qualsiasi d, siete capaci di dividerlo in 7 parti uguali utilizzando solo riga e compasso?

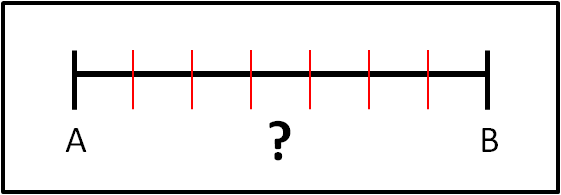
Esiste un metodo veramente rapido che ci servirà nel seguito della nostra descrizione. Prima di andare avanti, perciò, descrivetemi questo metodo, un metodo che era ben conosciuto dagli antichi greci.

N.B.: Dato che il "fomentatore" di questa serie di articoli è stato Frank, lui è OBBLIGATO a dare la risposta, anche se so che non ama molto i quiz... Ciò ovviamente non toglie la possibilità di rispondere anche agli altri lettori.

SOLUZIONE:

Da buon giocatore di golf, il nostro Frank ha cercato di evitare l'ostacolo provando a raggirarlo, magari con qualche tiro ad effetto. Operazione del tutto inutile, però... bastava ricordare uno dei teoremi più famosi tra quelli  dimostrati dagli antichi greci, quello di Talete. Abbiamo già visto come lui sia tato capace di eseguire moltiplicazioni e divisioni con le sue parallele tagliate da due trasversali. E, allora, perché non usare il suo genio per dividere un segmento di lunghezza PREDIFINITA d in n parti uguali, utilizzando, ovviamente, solo riga non graduata e compasso?

Come dice Leandro, basta considerare una qualsiasi retta r che passi per l'estremo A del nostro segmento e poi, facendo centro in A, riportare sulla nuova retta r, mediante il compasso, un segmento di lunghezza s qualsiasi. In tal modo otteniamo il punto A1. Facendo centro in A1 e raggio A1A (s), determinare un nuovo punto A2 e via dicendo in modo da ottenere sulla nuova retta tanti punti A,A1, ....., An. Ciò si può fare dato che non abbiamo nessun vincolo sulla lunghezza del segmento AAn. A questo punto Talete ci dà immediatamente la soluzione: congiungiamo An con B e poi tracciamo da An-1,..., A1 le parallele ad AnB (sappiamo già che tracciare una parallela a una retta da un punto qualsiasi è cosa fattibile con riga e compasso). Queste parallele intersecano il segmento originario di lunghezza d in tanti segmenti, tutti uguali, il cui numero totale sarà proprio n. In altre parole, abbiamo diviso il segmento AB in n parti uguali. Ribadiamo ancora che la seconda retta e l'apertura del compasso r sono del tutto arbitrari!

Adesso possiamo passare a qualcosa di più generale, anche se, come diceva Gauss, non può che essere un po' approssimato...