Questo primo metodo per la costruzione di un poligono regolare di n lati qualsiasi potrebbe anche essere tradotto in: "Gli ingegneri sanno poco di geometria". Il che sembrerebbe una vera assurdità, ma questo è quello che si percepisce da parecchi video che si trovano nella rete. In altre parole, o vengono considerati dei creduloni oppure dei rozzi geometri. Parole un po' sibilline che faremo in fretta a spiegare...

Qual è il problema che ci poniamo? Dato un certo segmento di lunghezza L, costruire tutti i poligoni regolari che abbiano lato L. Ovviamente, facendo uso soltanto di riga non graduata e di compasso, come abbiamo già esaurientemente spiegato.

Il succo di tutto è ricordare che qualsiasi poligono regolare è iscrivibile in un cerchio.

Già a questo punto si commette il primo errore: si presenta un metodo costruttivo che sembrerebbe rispondere allo scopo prefissato, ben sapendo che NON tutti i poligini regolari sono costruibili, come dimostrato nientemeno che da Gauss. Furbescamente, però, non si dice niente e, quindi, si accetta, in qualche modo, che gli ingegneri non conoscano Gauss...

Andiamo pure avanti e utilizziamo la Fig. 1 in cui si lavora correttamente con riga non graduata e compasso "molle" o "a scatto", come preferite chiamarlo.

Partiamo tracciando un segmento AB di lunghezza L. Facendo centro in A e B tracciamo due cerchi di raggio uguale a L. Essi si incontrano nel punto 6. Il triangolo A6B è equilatero per costruzione, per cui l'angolo A6B è uguale a 60°. Ricordando che l'angolo al centro di un poligono regolare è uguale a 360° diviso il numero dei lati, ne segue che AB è proprio il lato dell'esagono inscritto in un cerchio di raggio uguale ad AB = L (360/6 = 60) e centro 6. L'esagono si costruisce facilmente facendo centro col compasso in B e tracciando il cerchio di raggio AB = L. Dove esso incontra il cerchio di centro 6 e raggio L vi è un vertice C₆ dell'esagono. Si continua facendo centro in C6 e raggio C₆B e via dicendo fino a completare l'esagono. Quello che ci importa veramente è avere individuato il centro 6. E' anche immediato determinare il punto M, dato che basta tracciare da 6 la perpendicolare ad  AB (operazione ben nota con riga e compasso).

Consideriamo, adesso, la Fig. 2, in cui si disegna nuovamente il segmento AB = L.

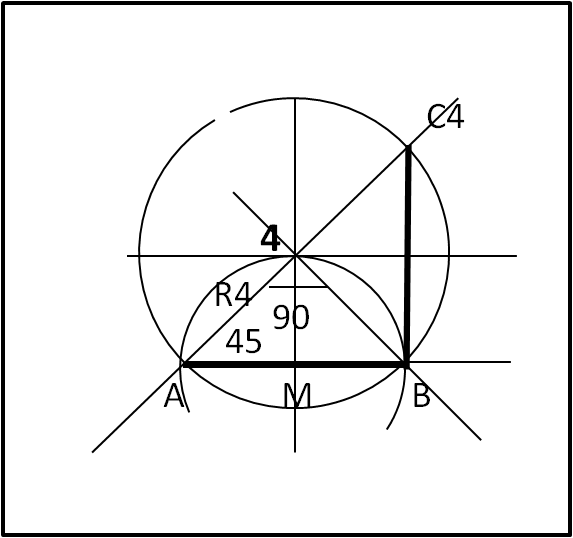
Facendo centro nel punto M tracciamo la circonferenza di raggio pari ad AM =MB. Essa interseca la perpendicolare al segmento AB, passante per M, nel punto 4.  L'angolo A4B deve essere di 90°. AB è quindi il lato del quadrato inscritto nel cerchio di raggio pari ad A4 e centro 4. Il quadrato si costruisce facilmente facendo centro in B e con raggio BA intersecare la circonferenza suddetta. Otteniamo C₄ e poi facendo centro in C₄ si continua fino a completare il quadrato. Ciò che è veramente importante è avere determinato il centro 4.

Non ci resta, adesso, che sovrapporre la Fig. 2 alla Fig. 1 e ottenere la Fig. 3, in cui si evidenziano soltanto i due punti 4 e 6, centri dei due cerchi circoscritti all'esagono e al quadrato di lato AB = L, e la perpendicolare ad AB tracciata dal punto M, lungo la quale si trovano 4 e 6.

Fino a qui tutto perfetto sia per l'utilizzo di riga e compasso, sia per la geometria. In altre parole, tracciando i cerchi di raggio 6A e raggio 4A con centri in 6 e 4, rispettivamente, otteniamo i cerchi circoscritti all'esagono e al quadrato di lato AB = L. Poi basta riportare AB sul primo cerchio per costruire l'esagono e sul secondo cerchio per ottenere il quadrato.

A questo punto, se non fossimo vincolati da riga e compasso, avremmo già capito quanto sia facile costruire qualsiasi poligono di lato L. Basterebbe considerare la Fig. 4 e imporre che ogni centro n dei cerchi circoscritti ai vari poligoni di lato L debba formare un triangolo nAM in cui l'angolo AnM sia pari a 360/2n.

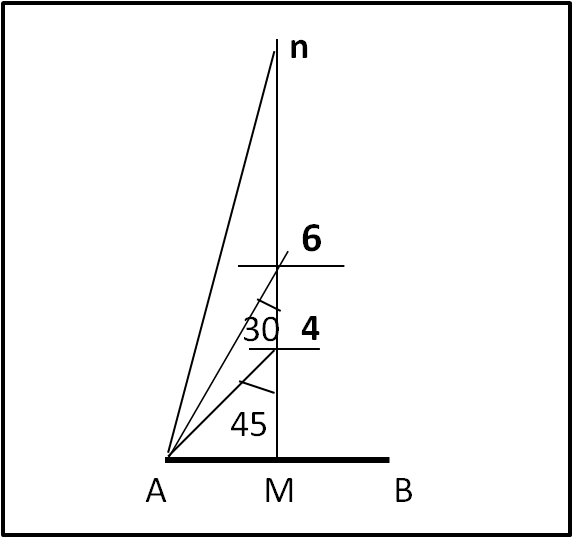
Infatti nel caso di 4 abbiamo proprio che A4M = 45 = 360/(4 · 2) = 360/8 e nel caso di 6 abbiamo A6M = 30 = 360/(6 · 2) = 360/12.

In parole più matematiche:

AM/Mn = tan(360/2n)

Mn = AM/tan(360/2n) = AB/(2 tan (360/2n))

dove AB = L è una costante e Mn individua il rispettivo centro del cerchio circoscritto al poligono di n lati di centro n.

Possiamo porre L = 1 e avere una semplice formuletta che ci permette di risolvere il problema per ogni valore di n, con buona pace di Gauss, in quanto abbiamo abbandonato l'uso obbligatorio di riga e compasso.

Mn = 1/(2 tan(360/2n))               .... (1)

Tuttavia, questo non è possibile e dobbiamo  seguire un metodo conforme alla regola "greca". Teniamoci, però, molto stretta la formuletta appena trovata in quanto ci servirà per valutare l'approssimazione che saremo costretti ad accettare.

Ed eccoci alla seconda "presa in giro" degli ingegneri... Torniamo alla Fig. 3 e riproponiamola nuovamente in Fig. 5.

Sappiamo che a metà tra 4 e 6 ci deve stare il punto 5. Banale. Facendo centro in 4 e 6 tracciamo le circonferenze di raggio 46 che si incontrano nei punti P e Q. Il segmento PQ è l'asse del segmento 46, perciò dove incontra la retta verticale passante per M è proprio il punto a metà tra 4 e 6, per cui possiamo chiamarlo 5. Poi il gioco è semplice: con centro in 4 e raggio 45 determiniamo il punto 3; con centro in 6 e raggio 65 determiniamo il punto 7 e via dicendo con 8, 9, 10...

Non resta che disegnare per ogni centro n così individuato la circonferenza di raggio nA: essa è la circonferenza che che ha come poligono inscritto il poligono regolare di lato L = 1. Nessun problema , quindi. Se n = 3, 4, 5,...19, 137 -o quello che volete- la costruzione risulta veramente banale.

Gli sprovveduti in geometria (gli ingegneri appunto) non devono fare altro che crederci ed essere convinti di avere determinato tutti centri da 3 a n dei cerchi che circoscrivono poligoni di lato L = 1, utilizzando solo riga e compasso e mandando al diavolo il povero Gauss.

Bellissimo veramente... peccato che le cose non vadano proprio così. La formuletta (1) prende le parti di Gauss e trova il baco della costruzione. Essa infatti ci permette di determinare le distanze tra M e i vari centri in modo ineccepibile. E' molto semplice confrontare questi centri VERI con quelli ricavati dividendo a metà il segmento 46 (trovando 5) e poi aggiungerlo al punto 6 fino a quando si vuole. Analogamente, si può togliere al punto 4 e trovare il punto 3.

Non sarebbe male fare questa piccola e noiosa (ma doverosa) operazione. Magari alcuni ingegneri meno creduloni ci sono subito arrivati, confrontare i centri VERI con quelli costruiti a distanza costante, che possiamo chiamare APPARENTI.

Si costruisce in modo semplice la Tabella che segue, dove si riportano il numero n dei lati del poligono, l'angolo al centro aV, VERO, la distanza tra i centri e il punto M calcolata con la formula VERA (MnV) e la distanza calcolata col metodo della divisione per due per trovare il punto 5, ossia la distanza APPARENTE MnA. Infine si ricalcola l'angolo al centro aA assumendo come vera la distanza apparente...

Molto bene... come si vede le distanze e gli angoli apparenti sono in realtà APPROSSIMATI. Per un poligono di 16 lati l'angolo al centro differisce di 0.7° e continua a crescere. Per un poligono di tre lati, la differenza è ben maggiore, quasi 3°.

Il metodo sarebbe anche piuttosto valido se si indicasse chiaramente che è una buona approssimazione. E, invece, essendo normalmente diretta agli ingegneri, si preferisce tacere, forse pensando che la prenderanno per buona. L'evidente "malafede" è abbastanza chiara, dato che in uno dei tanti video esplicativi si dice che a causa del tipo di costruzione è facile che si commetta qualche piccolo errore aprendo e chiudendo il compasso e cose del genere. Insomma la colpa è ancora una volta degli ingegneri e non del metodo approssimato.

Tra di noi ci sono molti validissimi ingegneri e sicuramente non si farebbero incantare da tante belle parole e da una costruzione abbastanza complicata. Probabilmente, questi ingegneri "faciloni" non sono di nazionalità italiana. O, almeno spero tanto... Voi, ingegneri di ben altra levatura, che ne dite?

Inserisco di seguito uno dei tanti video in inglese (terribile) e una pagina web in italiano, dove, purtroppo, non si fa accenno alla approssimazione.

 

Ma, ditemi in privato: "Perché odiate tanto Gauss?"

P.S.: Ovviamente, il mio è solo un soffio di ironia e conosco ormai troppo bene la bravura di tanti ingegneri che frequentano il nostro Circolo. Ciò che voglio veramente sottolineare è la faciloneria e la poca correttezza di certi siti web...

Continua...