Il quiz era forse più facile di quanto si potesse pensare a prima vista. I nostri Arturo e Paolo hanno capito subito la strategia da adottare, ma il primo si è accontentato di una conclusione un po' approssimativa (ah... questi ingegneri! Ai miei tempi li chiamavamo "quelli col regolo"), mentre il secondo ha raggiunto un risultativo quantitativamente esatto, ma con un numero di passaggi forse eccessivo. La migliore soluzione è quella di utilizzare entrambi gli approcci. Prima, mediante un grafico alla "Arturo" cerchiamo le caratteristiche geometriche della strategia vincente e, poi, attraverso le ovvie simmetrie che si manifestano, bastano un paio di equazioni veramente banali. In fondo, l'importante è solo sapere che la velocità è uno spazio diviso un tempo.

In Fig. 1, utilizziamo, allora, il diagramma spazio temporale presentato da Arturo e ci ragioniamo un po' sopra. La retta continua rappresenta il moto della ... moto (60 km/h); la retta tratteggiata, rappresenta il moto pedibus calcantibus (15 km/h).

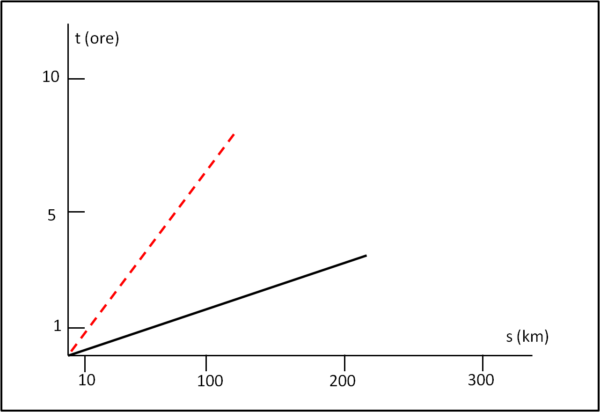
La soluzione più "cinica" sarebbe quella di estrarre a sorte chi può usare la moto e lasciare il terzo ad affrontare l'intero percorso a piedi.  Soluzione inutile allo scopo, dato che i tre fratelli devono essere tutti arrivati in città per entrare alla festa. Il poverino che se la fa a piedi impiega ben 300/15 = 20 ore per arrivare: la festa è già bella che finita!

Una soluzione che potrebbe apparire più sensata è quella di Fig. 2, linee nere, in cui B sale con A sulla moto.

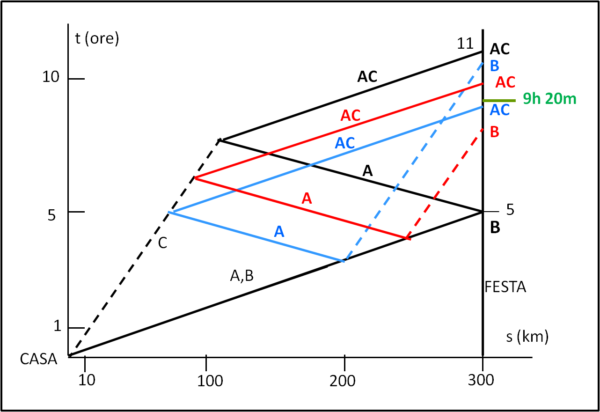
A lascia B in città  e torna indietro a prelevare C, che è partito insieme alla moto, ma a piedi. Proviamo a vedere quanto tempo impiegano A e C ad arrivare in città? Beh, è molto facile: A deve percorrere 300 km (per portare B) e poi 300 - x per prelevare C, dove x è lo spazio percorso da C a piedi, nello stesso tempo. Questo semplice ragionamento ci porta a scrivere che, al momento del loro incontro, il tempo t_CA necessario a C deve essere uguale al tempo t_AC = necessario ad A.

t_CA = t_AC

(300 + 300 - x)/60) = x/15

da cui si deriva che il tragitto x, fatto a piedi da C, è uguale a:

x = 600/5 = 120 km

Il tempo totale t_C impiegato da C (e quindi anche da A), per arrivare in città, è uguale a:

t_C = 120/15 + (300 - 120)/60  = 8 + 3 = 11 ore

Niente da fare... partendo alle 8 arriverebbero alle 19: troppo tardi!

Non vi è bisogno di fare tante altre prove "a casaccio", basta riflettere e capire che sono da scartare tutte le soluzioni in cui almeno uno dei tre fratelli PERDE TEMPO inutilmente (per questo nel titolo avevo scritto " non perdete tempo"...). Ciò capita tutte le volte che l'arrivo dei tre fratelli in città non è contemporaneo. Nel primo caso (linee blu)  sono A e C che, pur arrivando presto, devono aspettare, senza fare niente, che arrivi anche B; nel secondo caso (linee rosse) è B che deve aspettare l'arrivo di A e C. Ribadiamo, quindi che:

La soluzione migliore si ottiene non solo quando i tre fratelli partono assieme (cosa obbligatoria), ma anche quando i tre fratelli arrivano ASSIEME in città.

Tutti e tre, in tal caso, non stanno mai fermi inutilmente. Questo è il ragionamento fondamentale che, attraverso il grafico e i calcoli veramente irrisori, ci porta rapidamente alla soluzione che più ottimizza il tempo.

Ragioniamo sul grafico di Fig. 3, sfruttando  un minimo di geometria elementare.

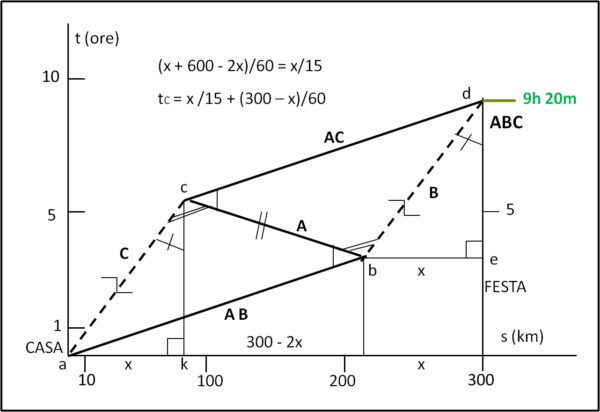
Imponiamo che i tre fratelli arrivino nello stesso istante in città. Ovviamente, due arrivano in moto e uno a piedi. E' anche vero che alla partenza la configurazione è la stessa, uno parte a piedi e due in moto. Salta subito all'occhio  una  simmetria ovvia, ma importantissima: i tratti percorso a piedi da B e da C devono essere uguali. I percorsi tratteggiati sono paralleli tra loro, così come lo sono anche i tratti continui che vanno da sinistra verso destra. Consideriamo allora i due triangoli abc e cdb. Innanzitutto, essi sono sicuramente dei triangoli, in quanto i percorsi  continui e a tratteggio si devono incontrare sia alla partenza che all'arrivo. Essi sono anche uguali in quanto hanno un  lato in comune e due angoli uguali (alterni interni di parallele tagliate da una trasversale). Ne segue che ac = bd. Analogamente, sono anche uguali i triangoli rettangoli ack e bde, dato che hanno due e il lato tra loro compreso (ac = bd) uguali. Ne risulta che be = ak.

Il percorso di 300 km viene, perciò, diviso in tre parti: due uguali a x e, quella centrale pari a 300 - 2x.

A questo punto, tutto diventa quasi immediato...

Calcoliamo x, dato che nello stesso tempo che A impiega a tornare da C, C si è mosso della distanza x. Dal grafico è ovvio dire che:

percorso di A fino al rilascio di B = 300 - x

percorso di A dal rilascio di B fino al prelievo di C = 300 - 2x

La somma di questi due percorsi è coperta con una velocità di 60 km/h.

Il tempo impiegato è, perciò:

tA = (300 - x + 300 - 2x)/60 = (600 - 3x)/60

Il tempo impiegato da C per essere prelevato è invece, molto più semplicemente:

tC = x/15

basta , quindi, uguagliare i due tempi e si ricava il valore di x.

tA = tC

(600 - 3x)/60 = x/15                      .... (1)

600 - 3x = 4x

7x = 600

x = 600/7 km

Possiamo fare a meno di calcolarlo... lo faremo alla fine

A questo punto abbiamo tutto ciò che ci occorre: il tempo impiegato da ciascuno dei tre fratelli deve essere sempre lo stesso (sono partiti assieme e arrivano assieme SENZA PERDERE TEMPO). Prendiamo, ad esempio, il fratello C.

Quanto tempo ha impiega ad arrivare in città? Presto detto: un primo tratto di x kilometri a velocità 15 km/h e un secondo tratto pari a (300 - x) in moto a velocità 60 km/h.

tC = x/15 + (300 - x)/60              .... (2)

tC = (4x + 300 - x)/60 = (3x + 300)/60 = (x + 100)/20

sostituiamo a x il suo valore pari a 600/7 km

tC = (600/7 + 100)/20 = 30/7 + 5 = 9.2857

tC = 9h 17m 8.5 s

Partendo alle 8, arrivano tutti e tre assieme alle 17 h 17 m 8.5 s

Per un pelo, ma ce la fanno!

La soluzione abbisogna soltanto della simmetria evidenziata dal grafico e di due semplici equazioni di primo grado. Non più di due asterischi, direi...