La difficoltà  di questo quiz geometrico sta -forse- in una soluzione che potrebbe sembrare controintuitiva. Dopo di che basta il semplice teorema di Pitagora...

Il punto chiave è che, essendo in geometria euclidea, sappiamo che la linea di minor distanza tra due punti deve essere misurata lungo la retta che li congiunge. Ne segue che la cosa migliore da fare è "aprire" completamente il nostro parallelepipedo, determinare un piano che contenga sia formica che zolletta e tracciare la linea retta che le congiunge. Tuttavia, vi sono vari modi di "aprire" il parallelepipedo...

In particolare, mentre le facce rettangolari hanno un solo modo per formare un piano, i due quadrati laterali possono restare uniti sia alla faccia superiore, che a quella laterale, che a quella inferiore. Possiamo tranquillamente eliminare la faccia rivolta verso di noi dato che basta e avanza quella posteriore, per ovvie ragioni di simmetria. A seconda di come eseguiamo questa operazione individuiamo un piano in cui la posizione della formica e della zolletta cambiano drasticamente l'una rispetto all'altra. Sembrerebbe naturale pensare che meno rettangoli vengano coinvolti nella traiettoria rettilinea finale, più corta dovrebbe essere la distanza. E, invece, non è affatto così. Meglio di tante parole vale la pena passare a una descrizione grafica.

In Fig. 1  ruotiamo i due quadrati verso l'esterno e utilizziamo il piano formato dai due quadrati e dal rettangolo posteriore.

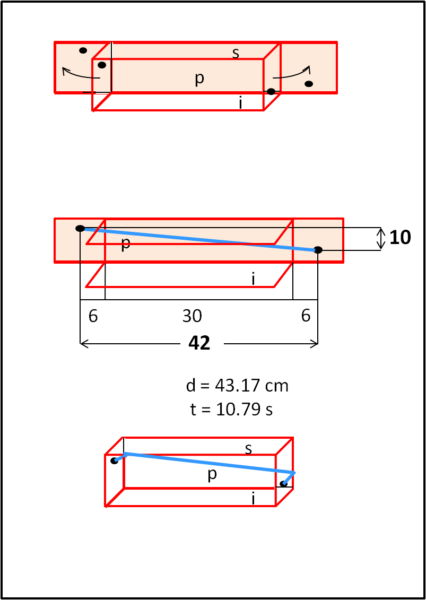
Questo piano è stato colorato in rosa. Non ci vuole molto a tracciare FZ e calcolarne la  lunghezza mediante il teorema di Pitagora. Ne segue che:

FZ = 43.17 cm

che equivale a un tempo:

t_FZ = FZ/v_F  = 43.17/4 = 10. 75 s

Niente da fare, la mosca arriva prima!

Nella parte bassa della figura vediamo il cammino della formica dopo aver richiuso la scatola.

Passiamo alla Fig. 2.

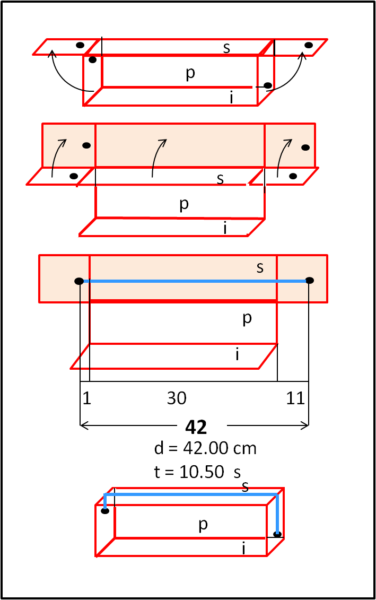
Ribaltiamo i due quadrati di 90° fino a farli appartenere al piano della faccia superiore. Poi ruotiamo il tutto sullo sfondo, individuando un nuovo piano in cui tracciare la congiungente FZ. Questa volta il percorso è veramente banale, essendo nient'altro che una linea retta parallela allo spigolo lungo dei rettangoli. Non c'è nemmeno bisogno di Pitagora, dato che la distanza FZ risulta:

FZ = 42 cm

t_FZ = 10.5 s

Un netto miglioramento, ma non basta ancora! La mosca arriva ben mezzo secondo prima sulla zolletta.

Fino ad ora abbiamo solo utilizzato una faccia rettangolare e due quadrate piegate in modo diverso. Passiamo ora a una "apertura" apparentemente più complicata che permette alla formica di passeggiare su due facce rettangolari oltre che su quelle quadrate.

Lo vediamo in Fig. 3.

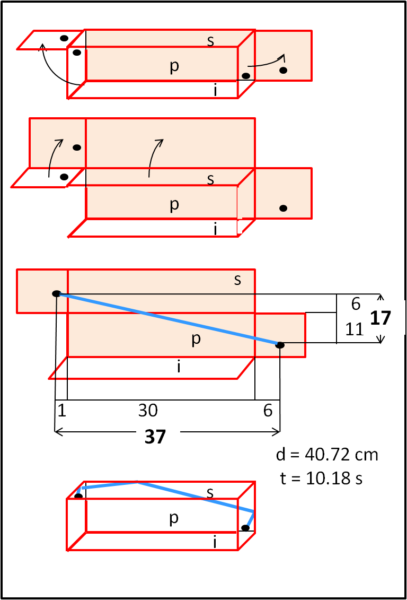
Il quadrato di sinistra viene fatto coincidere con il piano della faccia superiore, mentre quello di destra viene fatto coincidere con il piano della faccia posteriore. Poi ribaltiamo il piano superiore fino a formare un un unico piano con quello della faccia quadrata di destra e della faccia posteriore. Il piano rosa, questa volta, contiene due rettangoli e non uno solo. Non è certo difficile tracciare la congiungente FZ.

Magnifico, la distanza diminuisce ancora:

FZ = 40.72 cm

Purtroppo, però, ciò comporta che il tempo impiegato risulti:

t_FZ = 10.18 s

Per soli 8 centesimi di secondo la mosca arriva prima della formica.

Devo dire la verità... questa volta la formica voleva quasi arrendersi, ma poi si è detta: "Ho usato due rettangoli e il tempo è diminuito. Perché non provare con tre rettangoli? Tentar non nuoce, anche se sembrerebbe un tentativo inutile.

Rappresentiamo quest'ultima soluzione in Fig. 4.

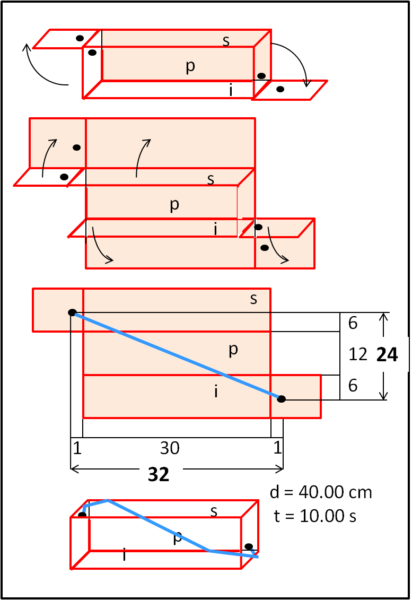
Il quadrato di sinistra lo ribaltiamo facendolo coincidere con il piano della faccia superiore, mentre quello di destra lo ribaltiamo fino alla faccia rettangolare inferiore. Poi ribaltiamo il piano superiore e quello inferiore fino a farli coincidere con il piano di sfondo. Non ci resta che tracciare la congiungente FZ che, questa volta, attraversa ben tre rettangoli.

Sembrerebbe una manovra inconcludente, ma... attraverso il solito Pitagora, otteniamo:

FZ = 40.00 cm

e il tempo necessario diventa:

t_FZ = 10.00 s

Mamma mia! La formica ce l'ha fatta ancora una volta riuscendo a raggiungere la zolletta con 10 centesimi di anticipo rispetto alla mosca. E poco importa se il cammino da fare, a scatola chiusa, sembrerebbe pieno di complicazioni e di cambi di direzione.

Allego anche una figura preparata dal nostro Arturo (che ringrazio di cuore) attraverso geogebra...

Ah, dimenticavo...La posizione della mosca e del foro nella parte superiore della scatola non hanno alcuna importanza. Li avevo aggiunti solo per cercare di creare un po' di confusione...Sapete come sono fatto...