Rinfrescata la memoria sulle proprietà della somma e differenza di vettori, affrontiamo un interessantissimo problema che, nuovamente, potrebbe essere stato enunciato dagli antichi greci. Invito caldamente i più esperti, in attesa del cenone di Capodanno, a tentare di dare la soluzione in modo autonomo, magari indicandomela nei commenti. Vi assicuro che è un bellissimo gioco geometrico!
Prendiamo 4 punti a caso nel piano e uniamoli per formare un quadrilatero. In realtà, si potrebbero anche intersecare le linee e la conclusione non cambierebbe. Limitiamoci, però, solo a un quadrilatero convesso, pur sapendo che non è assolutamente un vincolo.
Costruiamo su ogni lato un quadrato (ma potrebbe anche essere un rombo o un rettangolo) e indichiamone il centro, ossia il punto d'incontro delle rispettive diagonali. Siamo essi i punti Q1, Q2, Q3 e Q4. L'enunciato del teorema dice:
Se congiungiamo i centri opposti dei quadrati, i due segmenti ottenuti sono SEMPRE perpendicolari tra loro ed hanno la stessa lunghezza.
Ancora una volta, sembra una vera magia, rafforzata dal fatto, già accennato, che il nostro quadrilatero può essere veramente qualsiasi.
La dimostrazione che segue è altrettanto "magica" e di una semplicità disarmante. Basta seguire le varie figure che ho fatto e il procedimento risulterà accessibile a tutti. Il vero problema è avere l'idea giusta e affidarsi ai ... vettori. La lascio nascosta per non togliere il piacere a qualcuno di tentare la dimostrazione in modo autonomo.
Iniziamo, costruendo il nostro quadrilatero di partenza, i quattro quadrati e le congiungenti i loro centri. Dobbiamo dimostrare che Q1Q3 è uguale a Q2Q4 e che questi segmenti sono perpendicolari tra loro (Fig. 1).
Figura 1
Noi vogliamo dimostrare l'enunciato del teorema utilizzando solo la somma di vettori.
Iniziamo con una considerazione piuttosto semplice. Se tracciamo da ogni centro dei quadrati la perpendicolare al lato del quadrilatero su cui è costruito, possiamo essere sicuri che questo segmento (verde) divide a metà, per costruzione, il lato del quadrilatero (Fig. 2). Inoltre, essendo dei quadrati, queste metà sono uguali rispettivamente al segmento verde.
Figura 2
Introduciamo, allora, un po' di vettori. Innanzitutto il vettore a che ha come modulo la metà del lato del quadrilatero. Per cui su tale lato sistemiamo due di questi vettori. Analogo procedimento per gli altro quattro lati. Poi, prendiamo il vettore a, lo duplichiamo e lo ruotiamo in senso antiorario di 90°, ottenendo così il vettore a'. Ripetiamo le stesse operazioni per tutti e quattro i lati, ottenendo la Fig. 3.
Figura 3
Bene, adesso possiamo eliminare tutte le linee che non c'interessano più e lasciare in evidenza solo i vettori così introdotti e i due segmenti Q1Q3 e Q2Q4, che possono essere considerati anch'essi come vettori (Fig. 4).
Figura 4
Ognuno di loro può essere espresso come somma di vettori. Iniziamo da Q2Q4, come mostra la Fig. 5, iniziando da Q4 e finendo in Q2.
Figura 5
Possiamo scrivere che il vettore Q2Q4 è dato dalla seguente somma di vettori :
Q2Q4 = - a’ + a + b + b + c + c’
Il primo vettore è cambiato di segno dato che viaggia in verso opposto a quello originario.
Facciamo lo stesso con il vettore Q3Q1 (Fig. 6).
Figura 6
Q3Q1 = - b’ + b + c + c + d + d’
Anche adesso abbiamo cambiato di segno al primo vettore in quanto va in verso opposto all'originario.
Ricordiamoci bene che cosa vogliamo dimostrare: i vettori Q2Q4 e Q3Q1 sono perpendicolari e hanno la stessa lunghezza (ossia lo stesso modulo).
Se vogliamo provare che due rette (o due segmenti) sono perpendicolari possiamo ruotarne una di 90° e provare che essa è parallela all'altra.
Noi facciamo proprio questo! Prendiamo il vettore Q3Q1, con tutti i vettori che lo compongono, e lo ruotiamo di 90° in senso antiorario., come mostra la Fig. 7
Figura 7
Notiamo bene che, facendo questa operazione, i vettori componenti Q3Q1 hanno cambiato nome, come si può facilmente vedere anche confrontando il nuovo vettore ruotato con la Fig. 4.
Q3Q1 = b + b’ + c’ + c’ + d’ - d
Andiamo a riprendere il vettore Q2Q4, con tutte le sue componenti, e disegniamolo vicino al nuovo Q3Q1. A causa della rotazione dobbiamo provare che Q3Q1 è parallelo a Q2Q4 e che essi hanno la stessa lunghezza (Fig. 8).
Figura 8
Ruotiamo Q3Q1 di 180° in senso antiorario. (Fig. 9)
Figura 9
Ancora una volta, però, le componenti di Q3Q1 hanno cambiato nome, ma in modo molto semplice, ossia cambiando solo il loro segno, dato che abbiamo eseguito una rotazione di 180°. A questo punto abbiamo la Fig. 10.
Figura 10
Non ci resta che far combaciare Q1 con Q2, ossia fare, in altre parole, la somma tra il vettore Q2Q4 e il vettore Q3Q1 (Fig. 11)
Figura 11
Per quanto detto prima se il vettore finale risultasse uguale a zero, vorrebbe dire che i moduli dei vettori Q3Q1 e Q4Q2 sono uguali e che, ovviamente, i due vettori sono paralleli. Non lasciamoci ingannare dalla figura! Guardando lei, risulta ovvia la conclusione, ma ricordiamoci che dobbiamo provarlo e per farlo dobbiamo lavorare solo con le componenti e con i loro segni.
Cominciamo a semplificarla, ricordando le proprietà della somma vettoriale. Nella nostra "catena, abbiamo un b e un -b, uguali in modulo, ma contrari in verso, per cui possiamo eliminarli. Lo stesso anche con c' e - c', ottenendo la Fig. 12 di sinistra.
Figura 12
Una bella semplificazione, ricordando che, comunque, la somma vettoriale non è assolutamente cambiata: il risultato di questa catena deve rimanere lo stesso di quella precedente.
Tuttavia, possiamo anche spostare i vettori parallelamente a se stessi, cambiandogli la posizione nella catena, e ottenere la parte destra della Fig. 12. Attenzione ora! La somma di a, b, c e d è composta da vettori che sono ognuno la metà dei vettori introdotti nella Fig. 4, che è valida per definizione. Ma la somma di quei vettori era zero dato che tornavano al punto di partenza del quadrilatero che è chiuso su se stesso. Da cui deve essere zero anche la somma delle loro metà. Ne segue che:
a + b + c + d = 0
e può essere eliminato dalla figura.
Rimane l'ultima catena a' + b' + c' + d'... ma essa è composta da vettori, ognuno dei quali è stato ruotato di 90° rispetto a quelli che descrivevano il quadrilatero, ossia a', b', c' e d' sono proprio a, b, c e d ruotati di 90°. Ma se è zero la somma di a, b, c e d, DEVE essere zero anche la somma di a', b', c' d'. Possiamo eliminare anche loro... Rimaniamo con "niente" ossia abbiamo dimostrato che la lunga catena si chiude veramente su se stessa e, quindi, i vettori Q3Q1 e Q2Q4 hanno VERSO CONTRARIO ma UGUALE MODULO, il che vuol dire che i due vettori sono paralleli e quelli originari perpendicolari tra loro, oltre che avere la stessa lunghezza.
C.V.D.
Il teorema è stato formulato da Henricus Hubertus van Aubel nato a Maastricht (Olanda) il 20 novembre1830, insegnante di matematica presso il Royal Atheneum di Anversa. Le sue applicazioni sono state molteplici.
3 commenti
Noto che s'è divertito a estendere ai vettori un teorema già generalizzato e che usa le proprietà dei triangoli come base del teorema.
Un esercizio creativo non c'è ombra di dubbio.
Saluti.
Provo a rispondere.
I punti verdi sono i centri dei quadrati ed i punti arancio sono i centri dei lati.
I vettori in rosso sono uguali ai corrispondenti vettori in blu ruotati in senso antiorario di 90°.
Poichè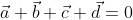 , allora anche
, allora anche 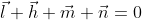 .
.
Voglio vedere se il vettore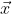 ruotato in senso orario di 90° è uguale a
ruotato in senso orario di 90° è uguale a 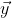 .
.
poiché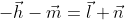 e
e =\vec{b}+2\vec{c}+\vec{d}) ,
,
dopo le sostituzioni l'espressione di è uguale a quella del vettore
è uguale a quella del vettore 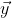
Quindi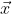 ed
ed 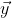 hanno la stessa lunghezza e sono perpendicolari tra loro.
hanno la stessa lunghezza e sono perpendicolari tra loro.
bravo Fabry! Nella soluzione vedrai che ho soltanto fatto qualcosa di simile, sempre graficamente...