Categorie: Matematica Riflessioni
Tags: quarto di cerchio quiz raggio Richard Feynman
Scritto da: Vincenzo Zappalà
Commenti:8
(Q) Attenzione Mr. Feynman ! * (con soluzione)
Dicono che addirittura Richard Feynman non abbia dato, per prima, la risposta migliore... Sarà vero oppur no? Comunque sia, proviamo a far meglio di lui!
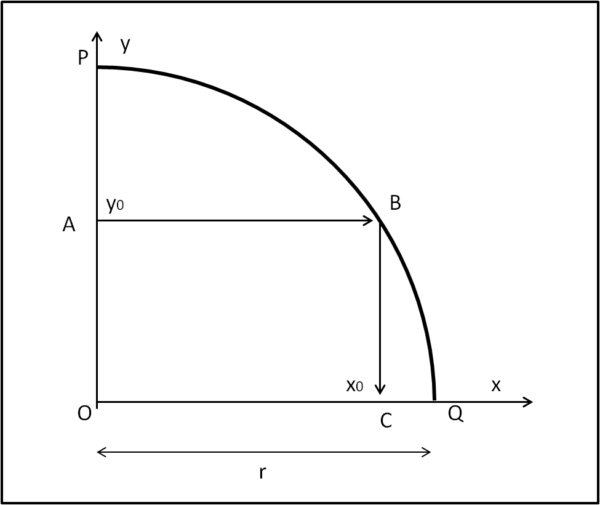
O sia l'origine degli assi x e y. Tracciamo un quarto di cerchio di centro O e raggio r qualsiasi. Da un punto A dell'asse y, di ordinata y0 < r, tracciamo la parallela all'asse x che incontri la circonferenza in B di coordinate x0 e y0. Da B tracciamo la parallela all'asse y fino a incontrare l'asse x in C, che ha, ovviamente, ascissa x0 (Fig. 1).
Tracciamo, infine la congiungente AC e indichiamo AP con a, CQ con c e AC con b (Fig. 2).
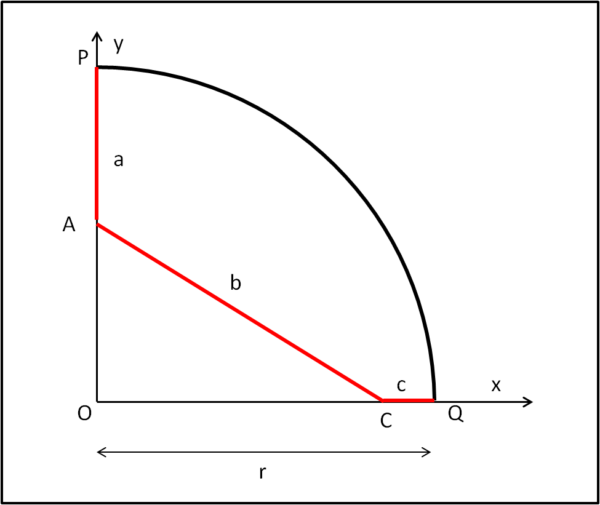
Determinare la formula più semplice che leghi il raggio r alle tre lunghezze a, b e c.
SOLUZIONE:
Andy ha sicuramente dato la risposta migliore e più rapida. Non c'è bisogno di nessun teorema di Pitagora: il segmento b è per costruzione la diagonale del rettangolo ABCO e quindi deve essere uguale al raggio. Insomma: r = b.
Va bene, torniamo seri...
Anno Nuovo... difficoltà nuove!






8 commenti
Caro Enzo ho sempre avuto un debole per Feynman, per cui dubito che non abbia dato la risposta migliore.
Invece l’ampiezza di probabilità che non sia io a dare al risposta corretta e migliore è piuttosto ampia.
Comunque la metto in bianco, per non influenzare negativamente gli altr@.
a = r – Y0
c = r – X0
b = √(r-c)² + (r-a)²
che ovviamente non è altro che:
b = √[r-(r-X0)]²+[r-(r-Y0)]² = √(X0²+Y0²)
Paolo
Non proprio l'errore di Feynman, ma quasi...
risposta in bianco
poiché b=R (diagonali rettangolo ABCO) applicando Pitagora al triangolo AOC ottengo :
(R-a)^2+(R-b)^2=R^2
da cui, svolgendo i calcoli alla fine ottengo:
R=a+c+radq(2ac)
In bianco, ma è troppo banale, ci dev'essere qualcos'altro.
Nel triangolo rett. AOC, per Pitagora:
(r-a)^2+(r-c)^2=b^2
Se si sovrappone la figura 2 sulla figura 1, AC è una delle due diagonali del rettangolo OABC e la soluzione è...... immediata e semplice
bene, bene...
direi che Andy ha dato la risposta migliore, senza bisogno di Pitagora
Va bene, ho scherzato... ma tra poco cominceremo a fare ...seriamente.
Tra parentesi, nessuno ha trovato la soluzione vettoriale dell'altro quiz, decisamente meno facile?