Categorie: Matematica Storia della Scienza
Tags: geometria sferica Menelao teorema dei seni trigonometria
Scritto da: Vincenzo Zappalà
Commenti:2
(QI) La trigonometria di Menelao **
Questo articolo è stato inserito nella pagina d'archivio "Antichi Greci, che passione!"ù
Una breve storia della trigonometria e un altro teorema dimenticato.
No, non vogliamo disturbare il mitico eroe della guerra di Troia, ma parlare di un altro Menelao, giustamente considerato uno dei padri dell'odierna trigonometria. Ma, dove, come e perché nasce la trigonometria, gioia e dolore di molti studenti? Vi era proprio bisogno di introdurre funzioni dai nomi così strani e un poco ambigui ? Parliamone...
La lunga storia della trigonometria
La trigonometria stabilisce essenzialmente delle relazioni tra grandezze angolari e grandezze lineari. Sicuramente queste relazioni erano conosciute in maniera rudimentale ed empirica già dagli egiziani, dato che dovevano saper misurare gli angoli tra piani (pensiamo, ad esempio alle piramidi e agli angoli tra le facce triangolari e il terreno). Per far ciò si limitavano a misurare i rapporti tra segmenti appartenenti ai due piani. Sicuramente un qualcosa già ben descritto nel 1650 a.C.
Tuttavia, la grande necessità di questi legami tra angoli (e, quindi, archi) e particolari segmenti era fondamentale nell'astronomia. Anzi, proprio i babilonesi, astronomi raffinati, avevano un gran bisogno di trattare con archi di cerchio appartenenti alla superficie sterica della volta celeste. In qualche modo, per essi, nasce prima la geometria sferica rispetto a quella piana, dato che quest'ultima rappresenta solo un modo per descriverla. Questa impellente necessità la possiamo vedere nella Fig. 1.
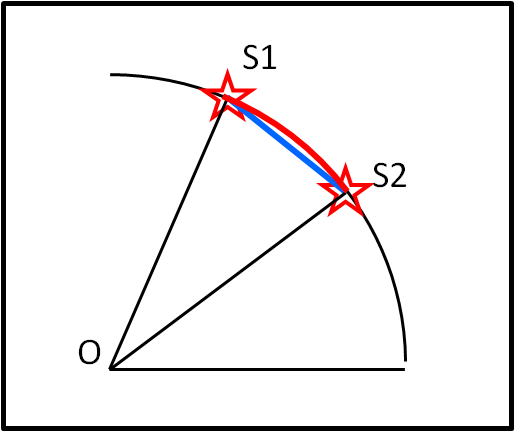
Le due stelle S1 e S2 proiettate sulla sfera celeste sottendono un arco di cerchio rosso. L'osservatore O, però, misura la distanza S1S2 (blu) su un piano. Gli studiosi di allora sapevano benissimo che S1 e S2 stanno su una superficie sferica, ma sapevano altrettanto bene che loro potevano solo osservare il segmento rettilineo S1S2.
La vera svolta si ha, però, con Ipparco di Nicea (secondo secolo avanti Cristo) che introduce una vera e propria funzione trigonometria, attraverso la misura della corda di un cerchio di raggio unitario corrispondente a un certo angolo α. In altre parole quello che oggi è rappresentato da 2 sen (α/2), come vediamo in Fig. 2.
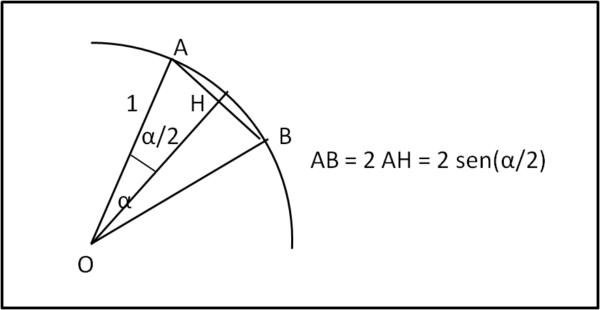
Egli determina i valori di queste corde e costruisce delle tabelle, che gli permettono di essere considerato come il vero fondatore della trigonometria. Non dimentichiamo, però, ancora una volta, che le culture orientali erano già ben consce dell'importanza di certi legami e in India si trova già il calcolo di un "seno" in un manoscritto che risale, più o meno, al settimo secolo a.C.
Bene, vediamo, allora come nasce l'attuale funzione "seno" e perché ha questo nome. Spesso le persone pensano che vi sia uno stretto legame tra la somiglianza della curva y = sen(x) e una delle forme più apprezzate del fisico femminile. Niente di tutto ciò. E nemmeno il nome ha a che vedere con un più generico significato di seno, come golfo, baia, insenatura. Il vero significato è proprio quello più banale che abbiamo appena descritto: seno = corda. Ci torneremo più avanti...
I greci non furono da meno e un grande matematico ed astronomo greco del primo secolo dopo Cristo ebbe molte geniali intuizioni. Egli scrisse trattati sulla geometria sferica ed enunciò teoremi in geometria piana che avrebbe poi applicato alle superfici sferiche. Il suo nome è lo stesso del grande re e condottiero di Sparta, Menelao, ma non ha niente a che spartire con lui. Oggi è noto come Menelao di Alessandria (mamma mia che meraviglia doveva essere l'Alessandria d'Egitto di quei tempi...).
Un teorema piano, ormai dimenticato
Un suo teorema di geometria piana è caduto ormai nel dimenticatoio, anche se è la base del teorema dei seni in geometria sferica. In poche parole. egli fu il primo a studiare espressamente un triangolo sferico. Egli, infatti, definisce come triangolo sferico, "lo spazio compreso tra archi di cerchio massimo sulla superficie della sfera". Possiamo ragionare più in grande, e vedere in lui ben chiara l'idea che la geometria piana non sia altro che una situazione particolare della geometria sferica. Concetto questo, che ci ha portato allo studio delle varie geometrie non euclidee e, perciò, alla possibilità di esprimere la concezione di uno spaziotempo curvo. La memoria non si può cancellare e perfino i più grandi Scienziati di ieri hanno dimostrato l'assoluto dovere di non dimenticare mai il passato. Ma qui si parla di grandi Scienziati e non di scienziati...
Torniamo a noi e vediamo di far tornare in auge l'ormai dimenticato teorema piano di Menelao. La sua dimostrazione è estremamente semplice e vale la pena richiamarla, proprio per ... non dimenticare.
Il teorema può essere enunciato in vari modi, ma noi abbiamo scelto la seguente:
Se i lati AB, BC, AC di un triangolo (o i loro prolungamenti) sono tagliati da una trasversale rispettivamente nei punti D, E, F, allora è verificata l'uguaglianza:
AD·BE·CF = BD·CE·AF
O, alternativamente:
AD/BD • BE/CE • CF/AF = 1
Come viene illustrato in Fig. 3
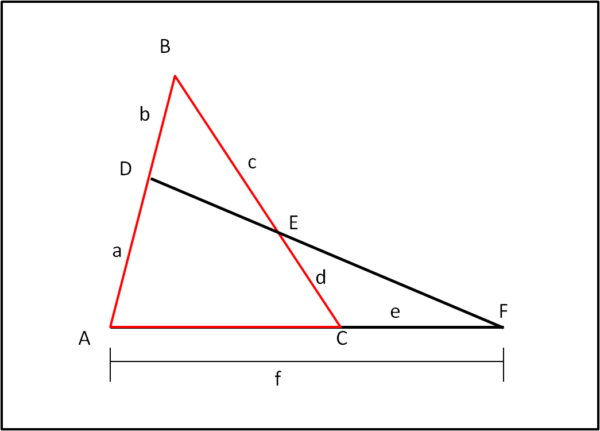
Abbiamo chiamato i vari segmenti con lettere minuscole per limitare la scrittura (ed evitare più facilmente errori, cosa che mi capita sovente...).
Riscriviamo la relazione precedente da dimostrare:
a • c • e= b • d • f
La dimostrazione è oltremodo facile e fa uso soltanto dei criteri di somiglianza dei triangoli. Mi vergogno, addirittura, di proporvela come "quiz". Riportiamola rapidamente...
Tracciamo, in Fig. 4, da C la parallela ad AB e identifichiamo così il punto K e i segmenti CK = g, EK = h, KF = i ed ED = j.
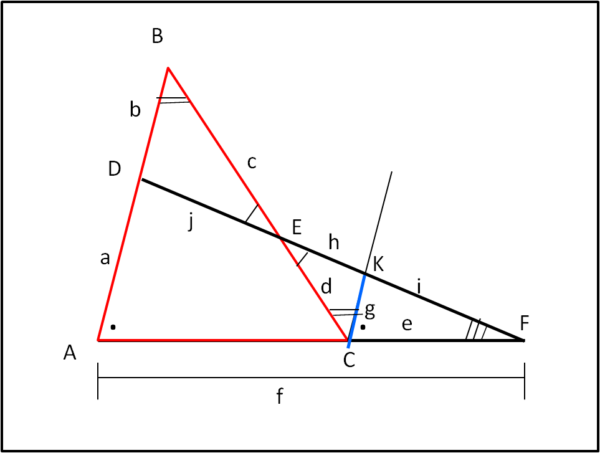
Individuiamo subito una coppia di triangoli simili: BDE e KEC. Ne segue che:
b/g = c/d = j/k
da cui
b • d = g • c
g = b • d/c .... (1)
Esiste, però, un'altra coppia di triangoli simili: ADF e CKF. Ne segue che:
a/g = f/e = (j + h + i)/i
da cui
a • e = f • g
g = a • e/f .... (2)
Eliminando g tra (1) e (2) si ottiene:
b • d/c = a • e/f
a • c • e = b • d • f
C.V.D.
Il teorema è stato il punto di partenza, per lo stesso Menelao, per passare a un triangolo sferico. Il nuovo enunciato dice:
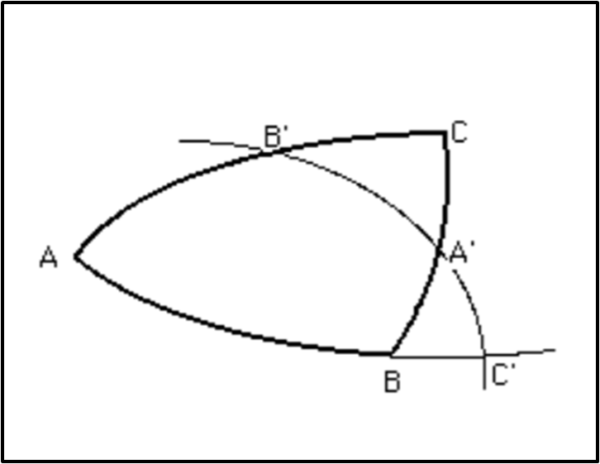
Se un triangolo sferico ABC è tagliato da una "retta", ossia da un cerchio massimo nei punti A', B', C', allora sussiste la relazione:
corda (2BA')/corda(2CA') • corda (2AB')/corda (2CB') • corda (2AC')/corda(2BC') = 1
Il significato di AB', CA', ecc. è quello di arco di superficie sferica, come mostra la Fig. 5.
Notiamo che le formule di geometria sferica sembrano ottenersi da quelle analoghe della geometria piana sostituendo le lunghezze dei
segmenti coi seni trigonometrici degli angoli corrispondenti. La cosa viene confermata per il "teorema dei seni", che fornisce, per un
qualunque triangolo sferico le analoghe relazioni. Con passaggi non difficili, che è inutile riproporre, si ottiene la celebre formula dei seni, scritta con le notazioni moderne:
segmenti coi seni trigonometrici degli angoli corrispondenti. La cosa viene confermata per il "teorema dei seni", che fornisce, per un
qualunque triangolo sferico le analoghe relazioni. Con passaggi non difficili, che è inutile riproporre, si ottiene la celebre formula dei seni, scritta con le notazioni moderne:
sen (AB)/sen(γ) = sen (BC) sen(α) = sen (CA) sen (β)
A questo punto non è difficile, anche se veramente contorto, risalire al nome "seno".
Arco e freccia: viva gli ... indiani!
In qualche modo gli scritti di Menelao giunsero in India. Essi furono tradotti e trasformati in una specie di scritto poetico, col titolo di SIDDHANTA. Proprio in quella versione poetica sembra che si faccia chiaro riferimento all'arco e alle frecce (come risulta evidente anche dalla nostra Fig. 2). Questi termini vennero, perciò, usati per descrivere il passaggio da piano a superficie sferica. In particolare, la parola sanscrita "jiva " significa "corda di un arco". La semi-corda del doppio arco (quella usata da Menelao) interveniva spesso e si decise di usare un termine abbreviato: "jiva" al posto dell'espressione più lunga "ardha jiva". Successivamente, gli arabi cercarono di tradurre questi testi, ma non trovarono nella loro lingua un significato per jiva, e, dato che il suono era lo stesso, la tradussero in "jiba ". Tuttavia, quando arrivò nelle mani dei traduttori europei, essendo "jjba" scritta come "jiab", che aveva il significato ben preciso di "cavità, tasca, insenatura", essi la tradussero col termine latino "sinus". In India e in seguito anche nella cultura musulmana la trigonometria fiorì e si sviluppo portando a molte delle relazioni che usiamo oggi. In Europa, finalmente, il grande Eulero ne diede una trattazione analitica e fu proprio lui a coniare le abbreviazioni sin, cos, tang, cot, sec, e cosec.
Piccolo QUIZ **
Terminata questa breve storia sull'origine della più celebre delle funzioni trigonometriche, fatemi tornare al teorema piano di Menelao. A fine '600, fu enunciato un teorema che suona così:
Dato un triangolo qualsiasi ABC, si traccino due rette dai vertici A e B che si incontrino nel punto O. Tracciando una terza retta dal terzo vertice C che passi per O, chiamando D, E ed F i punti in cui queste rette incontrano i rispettivi lati opposti del triangolo, si ha che:
AD/DB = BE/EC = CF/FA
come illustra la Fig. 6
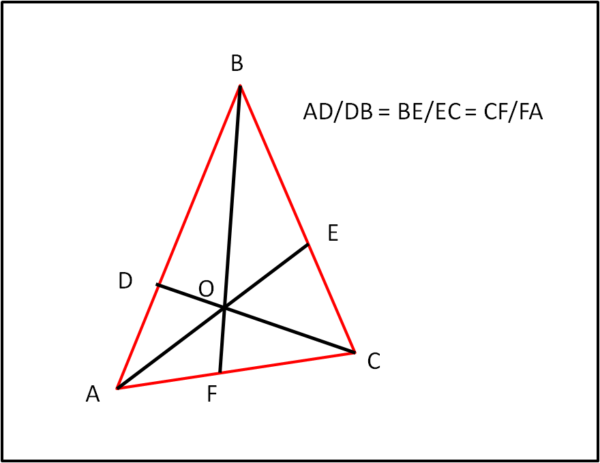
Bene, vi chiedo solo di dimostrarlo attraverso l'utilizzo del teorema di Menelao. Un problema veramente semplice, ma che fa parte anch'esso della storia della Scienza.






2 commenti
Eratostene di Cirene fece a suo tempo uso dei concetti di trigonometria per determinare l'ampiezza dell'angolo la cui funzione (sen0) è il rapporto tra l'altezza dello gnomone e la distanza orizzontale ?
caro Massimo,
I greci non espressero direttamente la funzione seno, ma il rapporto tra angoli e corde era già ben noto. Oltretutto, il seno aveva già fatto la sua comparsa in India attorno all'ottavo secolo avanti Cristo e -forse- i babilonesi avevano creato tabelle sulla relazione tra corda e angolo. La vera idea geniale di Eratostene è stata soprattutto l'aver ipotizzato i raggi del Sole paralleli e la Terra sferica.