La serie completa "Dall'Atomo alle stelle e viceversa" è disponibile QUI

 

Per la campana e il suo "picco" conta solo la temperatura

Anche se in modo abbastanza empirico, è stato possibile, già nella seconda metà dell’ottocento, descrivere, con due semplici formule, la dipendenza della luce emessa da un corpo nero in funzione della temperatura raggiunta. In particolare, si è stabilito che l’energia  totale della luce emessa per unità di tempo (ossia la potenza) è proporzionale alla quarta potenza della temperatura. In parole matematiche:

E = σ T⁴

dove σ è una costante. Più esattamente, si ricava che il numero di fotoni emessi nel’unità di tempo va con il cubo della temperatura, mentre la loro energia media dipende linearmente da essa. Moltiplicando numero di fotoni per la loro singola energia media otteniamo la quarta potenza enunciata prima. Questa legge prende il nome di legge di Stefan-Boltzmann e lo stesso nome viene dato anche alla costante σ.

Questa legge, importantissima, ci dice quanta energia si produce globalmente al variare della temperatura. Più la temperatura cresce e più energia si produce. Risultato abbastanza comprensibile e logico.

Fatta questa preliminare precisazione, possiamo ricavare un’altra legge empirica molto importante, ricordando che la capacità di oscillare di un fotone è legato alla sua energia. Tanto più è energetico è tanto più corto è il suo periodo di vibrazione e quindi anche la sua lunghezza d’onda. In semplici parole: energia e lunghezza d’onda di un fotone sono inversamente proporzionali. Tuttavia, abbiamo appena detto che l’energia di un fotone dipende in modo lineare dalla temperatura. Ne segue una relazione fondamentale per il corpo nero: tanto più grande è la temperatura tanto più piccola è la lunghezza d’onda. Questa relazione, chiamata legge di Wien, vale, in particolare, per la lunghezza d’onda in cui è massima l’emissione.  Questa legge ci dice che per ogni temperatura si ha un certo valore della massima radiazione luminosa. Sappiamo, però, che ad ogni lunghezza d’onda è associato un certo colore. Ne segue che a ogni temperatura è associato un ben determinato colore in cui si ha il massimo di emissione. La formula di Wien si scrive:

λ_max = k/T

dove k è una costante.

Parlando di massimo d’emissione in funzione della lunghezza d’onda non possiamo fare a meno di parlare, in modo più approfondito, dello spettro elettromagnetico del corpo nero, per una certa temperatura, mostrato in  Fig. 13. Esso, come già detto, non è altro che la distribuzione dell’intensità della luce emessa da un corpo nero in funzione della lunghezza d’onda. Proprio quella che si riesce a costruire analizzando la luce che esce dal famoso forellino. Gli esperimenti mostrano molto bene che essa segue una specie di campana, raggiungendo un valore massimo per una certa lunghezza d’onda. Variando la temperatura varia anche lo spettro, seguendo le due leggi appena formulate. Tuttavia, c’è qualcosa che non va…

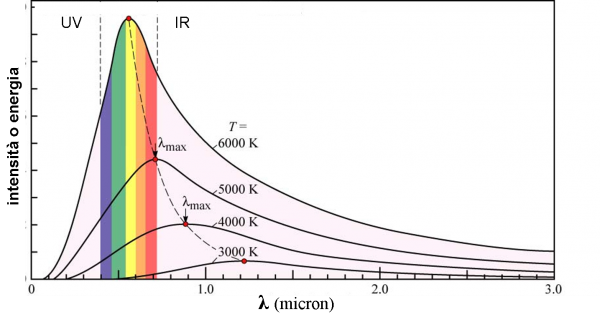
Ricapitoliamo brevemente: la legge di Stefan-Boltzmann dice che l’energia totale (quella dell’intera campana) è funzione della temperatura, mentre quella di Wien ci dice che il massimo di questa “campana” si sposta verso lunghezze d’onda maggiori per temperature decrescenti. Mettendole assieme, si può dire che la campana sposta il suo massimo verso lunghezze d’onda maggiori, per temperature decrescenti, e che la campana, nella sua totalità, si abbassa. Fin qui tutto bene, come mostra la Fig. 13.

Magnifico. Due leggi molto interessanti e molto utili per il nostro scopo, dato che legano molto bene temperatura, lunghezza d’onda ed energia luminosa. Tuttavia, sarebbe molto bello saper descrivere matematicamente la “campana”, osservata direttamente negli esperimenti. In altre parole, cercare di andare oltre alla legge di Stefan-Boltzmann, e calcolare teoricamente non solo l’energia totale, ma quella relativa a ogni singola lunghezza d’onda.

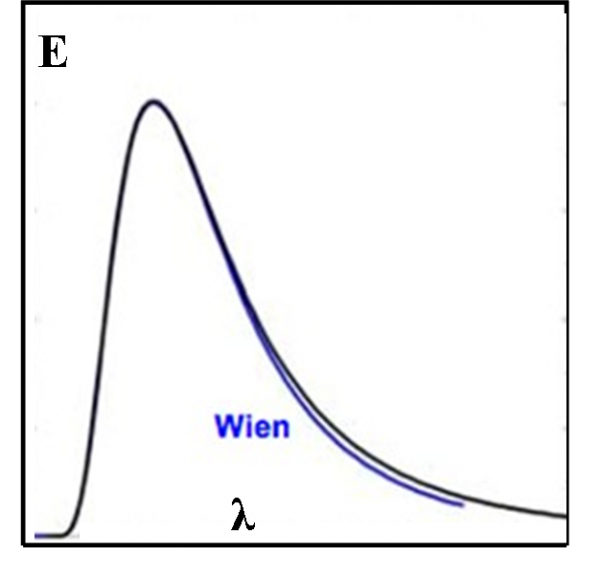
Trafficando con le varie grandezze in gioco, Wien sembrava aver trovato una buona rappresentazione (Fig. 15). Purtroppo, però, andava bene per piccole lunghezze d’onda, ma falliva per grandi lunghezze d’onda. In qualche modo lui aveva lavorato su un gas composto da molecole, dato che ancora non si conoscevano le interazioni tra le particelle più piccole.

 

Una catastrofe infinita

Utilizzando la teoria elettromagnetica sviluppata da poco, si giunse anche a una legge teorica che stabiliva come l’energia della singola lunghezza d’onda dovesse essere direttamente proporzionale alla temperatura, ma inversamente proporzionale alla quarta potenza della lunghezza d’onda. Essa si chiama legge di Rayleigh-Jeans. Come già detto, essa è una legge teorica, basata sulle nuove teorie dell’elettromagnetismo e dovrebbe funzionare, a meno di non ammettere che le teorie così apparentemente perfette siano, invece, ben lontane dalla verità. Riportiamo questa formula teorica che, però,  non … funziona assolutamente:

ΔE = C T/λ⁴

Dove ΔE è l’energia relativa a un piccolo intervallo di lunghezza d’onda e C una delle “solite” costanti (da non confondere con c che è la velocità della luce!).

Essa va benissimo per lunghezze d’onda molto lunghe, ma per lunghezze d’onda sempre più corte (alte frequenze) porta a valori sempre più alti dell’energia. Teoricamente, per una lunghezza d’onda uguale a zero l’energia diventa infinita. E questo non si vede assolutamente negli esperimenti e nemmeno è un risultato ammissibile. La Fig. 16 ci mostra l’andamento che ci si aspetterebbe dalla legge teorica, confrontato con l’andamento reale di un corpo nero: una vera CATASTROFE per l’elettromagnetismo!

 

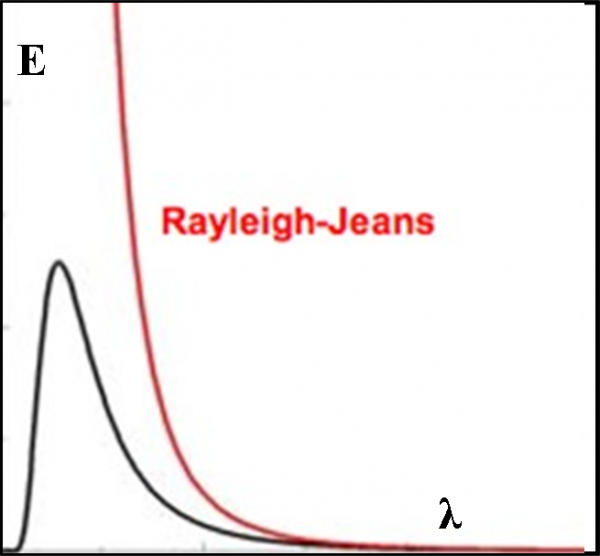
Dato che la parte, subito prima della minore lunghezza d’onda dello spettro visibile, prende il nome di ultravioletto, questo risultato assurdo venne chiamata proprio catastrofe ultravioletta.

Il corpo nero era una meravigliosa astrazione che permetteva di legare perfettamente l’energia dei fotoni (e quindi la luminosità) alla temperatura, ma la legge che doveva descrivere questa relazione sembrava portare a una vera “catastrofe” per le piccole lunghezze d’onda.

Tra poco, affronteremo di petto questa problematica che aprirà le porte, quasi senza volerlo, alla meccanica quantistica e al modello atomico di Bohr. Prima di partire in quarta, ragioniamo un attimo su quello che abbiamo ottenuto con il corpo nero e con la sua distribuzione in funzione della lunghezza d’onda, ossia lo spettro. Anche se non riusciamo a spiegarlo con la Fisica Classica, resta pur sempre un risultato fantastico, soprattutto se accompagnato dalle due leggi di Stefan-Boltzmann e di Wien. Vale la pena riproporre in Fig. 17, qualche spettro elettromagnetico di corpo nero, inserendo le lunghezze d’onda del visibile (ossia i colori dell’arcobaleno o del prisma di Newton). A sinistra del visibile abbiamo l’ultravioletto (UV) e a destra l’infrarosso (IR).

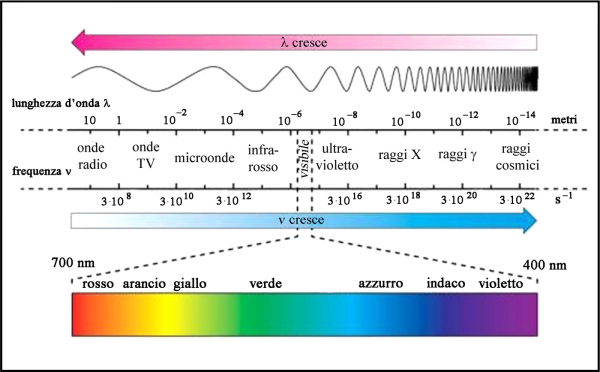
In realtà, lo spettro elettromagnetico è estremamente ampio e la parte visibile è una regione estremamente limitata, come vediamo nella Fig. 18.

 

La serie completa "Dall'Atomo alle stelle e viceversa" è disponibile QUI