Categorie: Matematica Teoria degli insiemi
Tags: Hotel di Hilbert Infiniti di Cantor insiemi numerabili
Scritto da: Umberto Cibien
Commenti:0
Gli infiniti di Cantor (3): Gli insiemi numerabili
In ricordo di Umberto Cibien, prematuramente scomparso, riproponiamo alcuni dei suoi migliori articoli.
Cardinalità di un insieme finito
Affermiamo intanto che un insieme è finito se riusciamo a contare il numero dei suoi elementi. Tale numero è proprio la cardinalità dell'insieme. Nell'articolo sulle corrispondenze, abbiamo visto come è possibile decidere in altro modo se due insiemi hanno lo stesso numero di elementi: basta che possano essere messi in corrispondenza biunivoca.
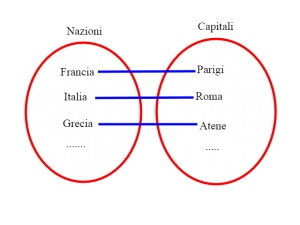
In questo esempio risulta chiaro che nazioni e capitali hanno lo stesso numero di elementi.
Cardinalità di un insieme infinito.
Nel caso di insiemi finiti, per decidere se hanno lo stesso numero di elementi ho dunque due possibilità:
1) contare il numeri rispettivi di elementi e vedere se sono uguali
2) vedere se possono essere messi in corrispondenza biunivoca.
Nel caso degli insiemi infiniti, non posso usare l'opzione 1), in quanto non so cosa voglia dire contare gli elementi di un insieme infinito(conta e conta non finirei ma i di contare).
Nulla mi vieta di usare però la seconda opzione: (dovuta a Cantor nel 1878)
Due insiemi infiniti sono ugualmente numerosi se esiste una corrispondenza biunivoca tra di essi.
Qui però pur sapendo che due insiemi sono ugualmente numerosi, non sappiamo quale sia la cardinalità di un insieme infinito. Possiamo provare a dare una prima risposta alla domanda di cosa sia il numero di elementi di un insieme A, che viene anche detto numero cardinale o cardinalità di A. Esso non è altro che ciò che hanno in comune tutti gli insiemi ugualmente numerosi ad A, ossia che possono essere messi in corrispondenza biunivoca con A. Tale cardinalità si indica con |A|.
L'Albergo di Hilbert.
Un prima caratteristica di un insieme infinito è che è possibile aggiungere un elemento all'insieme senza modificare la sua cardinalità. Vediamolo con un esempio dovuto ad Hilbert.
L'albergo ha infinite stanze che sono numerate come i numeri naturali(0,1,2,3,...). L'albergo è pieno, quindi i clienti sono tanti come i numeri naturali. Arriva un nuovo cliente; cosa si può fare? Si sposta ogni cliente presente nella camera successiva (quello della 0 nella 1,quello della 1 nella 2 e così via). Si mette il nuovo cliente nella camera 0 che si è liberata. Alla fine il numero dei clienti non è cambiato anche se ne ho aggiunto uno, in quanto è sempre uguale al numero delle camere. Se le camere fossero state in numero finito, non sarebbe stato possibile effettuare questa operazione; se si riflette sul concetto di infinito come a qualcosa di dinamico, non si entra in nessuna contraddizione.
Gli insiemi numerabili
Cominciamo con degli esempi. Consideriamo l'insieme dei numeri naturali N e l'insieme dei numeri Pari P. La funzione che a un numero naturale n associa 2n è una corrispondenza biunivoca fra N e P.
| 0 | 1 | 2 | 3 |
| 0 | 2 | 4 | 6 |
per ogni numero pari c'è uno e un solo numero naturale che lo genera.
Ma i numeri pari sono strettamente contenuti nei numeri naturali.
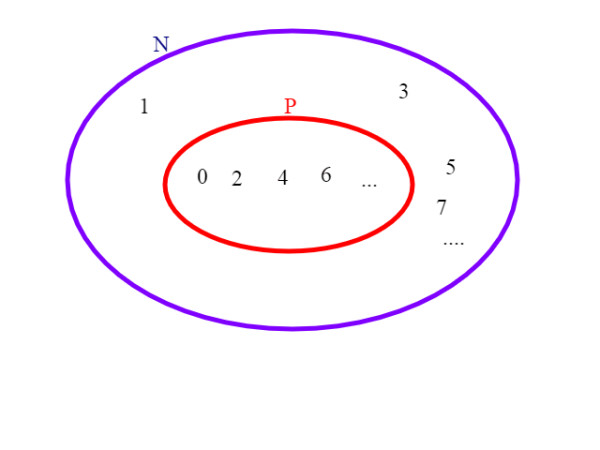
Gli insiemi che possono essere messi in corrispondenza con i numeri naturali si dicono anche insiemi numerabili.
Anche l'insieme dei numeri dispari è numerabile; basta associare ad ogni numero naturale il numero 2 n +1
| 0 | 1 | 2 |
| 1 | 3 | 5 |
ma anche l'insieme dei numeri dispari è strettamente contenuto nei numeri naturali.
Possiamo concludere che:
La parte non sempre è minore del tutto.
L'affermazione di Euclide "il tutto è maggiore di una qualsiasi sua parte" non è valida nel caso di insiemi infiniti. Anzi Dedekind prende da qui la sua definizione di insieme infinito:
si dice che un insieme X è infinito se esiste una corrispondenza biunivoca tra X ed un suo sottoinsieme proprio.
La cardinalità dell'insieme unione.
Dati due insiemi A ,B sappiamo cos'è l' insieme C definito come unione di A con B:
prendendo semplicemente per C tutti gli elementi che sono in A o in B.
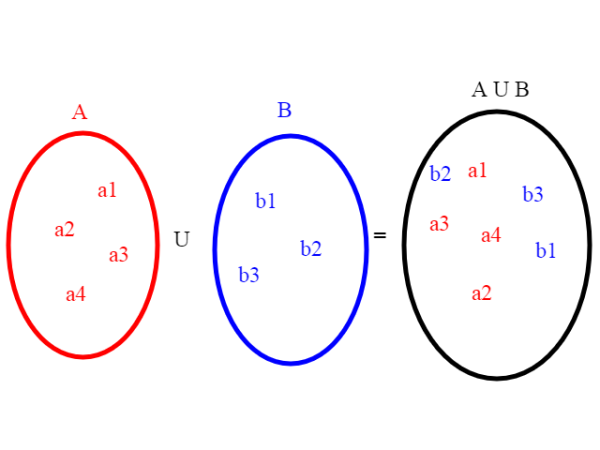
Supponiamo che A e B siano numerabili e che A e B siano disgiunti ovvero senza elementi in comune. Allora A può essere messo in corrispondenza biunivoca con i numeri dispari e B con i numeri pari, essendo entrambi numerabili. Ma i numeri pari più i numeri dispari danno tutti i numeri naturali;In tal modo abbiamo stabilito una corrispondenza biunivoca tra l'unione di A e B e N; quindi L'unione di due insiemi numerabili è numerabile.
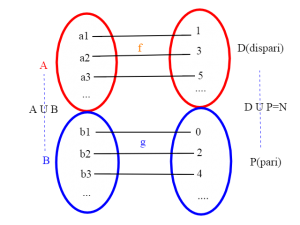
Vediamo di spiegare meglio questo fatto. Se A può essere messo in corrispondenza biunivoca con D (numeri dispari) chiamiamo f tale corrispondenza (f: A-->D). Allo stesso modo se B può essere messo in corrispondenza biunivoca con P (numeri pari) chiamiamo g tale corrispondenza (g: B-->P). A e B sono disgiunti (questo è fondamentale). Costruiamo un corrispondenza e(x) da A U B in N (pari più dispari) in tal modo:
e(x)=f(x) se x appartiene ad A
e(x)=g(x) se x appartiene a B
Essendo f,g biunivoche, anche e è biunivoca.
La cardinalità dell'insieme Z dei numeri relativi.
Perché abbiamo ricavato questo risultato? Vogliamo andare a vedere "quanti" elementi ha Z, insieme dei numeri relativi (che abbiamo visto nell'articolo sugli insiemi). Pensiamo a Z come unione di due insiemi A,B
A={0,1,2,3,4,...} B={-1,-2,-3,-4,...}
A non è altro che N ;
Indichiamo con N+={1,2,3,4,...} N privato dello zero, che è ancora numerabile, perché se associamo a n-->n+1 abbiamo una corrispondenza biunivoca fra N e N+ .
B può essere messo in corrispondenza biunivoca con N+ con la seguente funzione: -n . Allora abbiamo che Z è l'unione di due insiemi numerabili, quindi per quanto visto prima Z è numerabile.
Aleph 0 ( è il simbolo usato per indicare la cardinalità del numerabile.
Esso deriva dalla lettera dell'alfabeto ebraico aleph, che è la prima lettera dell'alfabeto.
Riassumendo:se indichiamo con |X| la cardinalità di un insieme infinito X, con P l'insieme dei numeri pari, D l'insieme dei numeri dispari, abbiamo che :
|N|= |P| =|D|=|Z|=( . Quindi gli insiemi che abbiamo trattato finora hanno tutti lo stesso ordine di infinito.
La prossima volta ci occuperemo della cardinalità di un altro insieme numerico famoso: Q (insieme dei numeri razionali)
Indice di tutti gli articoli di Umberto Cibien presenti in archivio-Matematica





