Questo articolo è inserito nella sezione di archivio Antichi Greci, che passione!

 

Questo apparente paradosso è attribuito ad Archimede, anche se sembrerebbe più ovvio essere opera di Galileo. Data l'inventiva e la capacità di rendere pratici esperimenti mentali non possiamo comunque stupirci più di tanto. I greci sì che sapevano usare il cervello! E dire che Archimede niente ancora sapeva della legge di gravità, ma le sue intuizioni lo portarono a precorrere i tempi. Forse, anche allora piacevano le "fake news" (intelligenti e utili, però).

Presento l'intera faccenda sia come esperimento mentale sia come esperimento pratico. Invito, perciò, i più abili a costruirsi da soli le componenti di quello che sembra ancora oggi una vera e propria assurdità fisica.

Cominciamo a costruire una specie di telaio, che altri non è che un vero e proprio piano inclinato. Qualche tavoletta di legno o anche di cartoncino un po' spesso e il gioco è fatto, come mostra la Fig. 1 (disegno schematico in 3d) e la Fig. 2 (visione dall'alto e di lato).

 

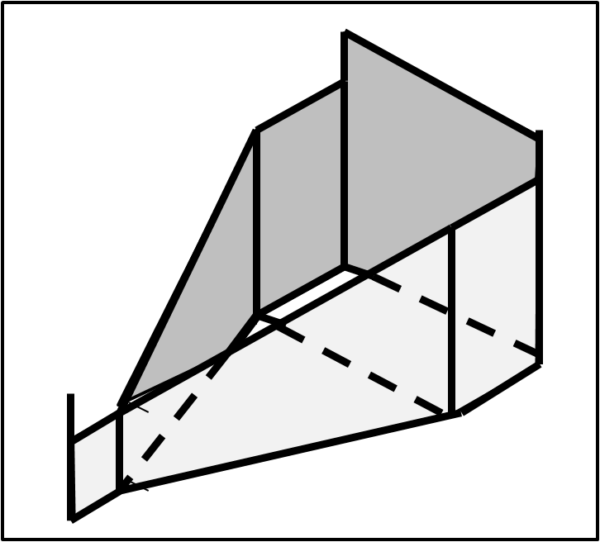
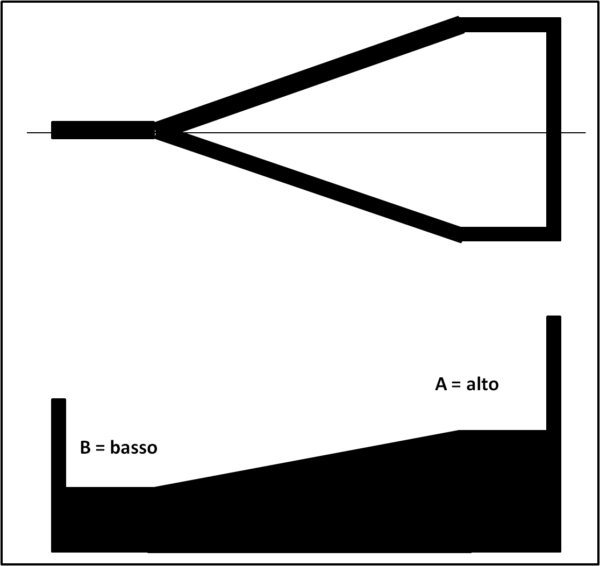
Bene... a questo punto costruiamo o recuperiamo, in qualche modo, un cilindro rosso che abbia un certo raggio di base e sistemiamolo nella parte alta (A) del telaio. Lasciamolo libero di muoversi e non ci stupiamo di certo se il cilindro scende rotolando verso la parte bassa (B), come mostra la Fig. 3.

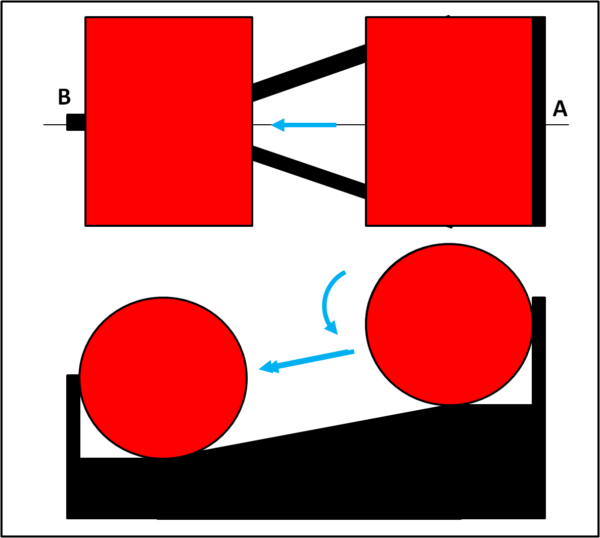
Galileo ci ha mostrato le meraviglie del piano inclinato e come esso sia capace di "rallentare" la caduta di un grave, permettendone lo studio del movimento.

Adesso, però, viene la parte un po' più complicata dal punto di vista pratico: la costruzione di una forma a doppio cono, che abbia il cerchio, in cui sono incollate le due parti, uguali al cerchio di base del cilindro (ma può essere anche più grande), come mostra la Fig. 4

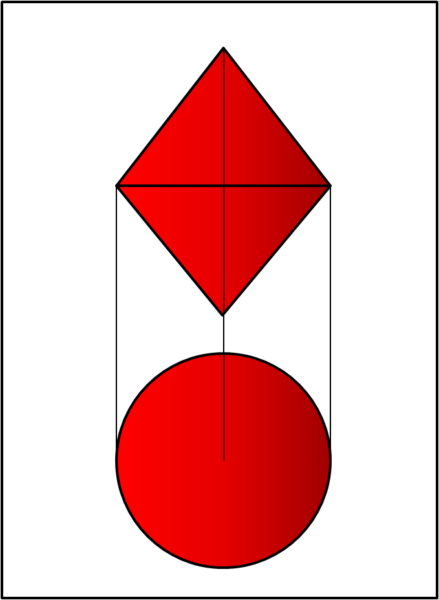
Fatto? molto bene... non ci resta che prendere il doppio cono e poggiarlo nella posizione A come fatto per il cilindro (Fig. 5).

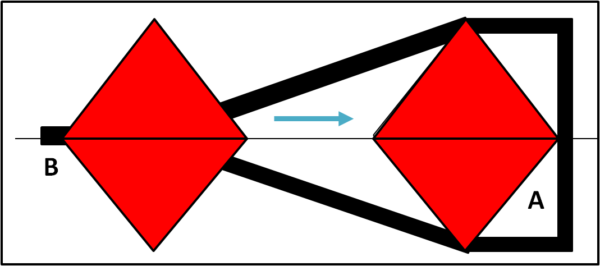
Non si muove? Beh... potrebbe essere l'attrito;  proviamo a dargli una leggerissima spinta. Eh no... sembra proprio non volersi allontanare dalla posizione A. Non ci resta che entrare nei panni di Alice e metterlo nella posizione bassa B. Come per incanto il doppio cono inizia a muoversi e si dirige sicuro e preciso fino alla posizione A. In poche parole il cono sta infischiandosene della gravità e, invece, di scendere per il piano inclinato, esegue l'azione contraria: SALE !

Il video che segue mostra quanto ho detto a parole e ripete quanto è successo con il modello che avete costruito voi (se ci siete riusciti).

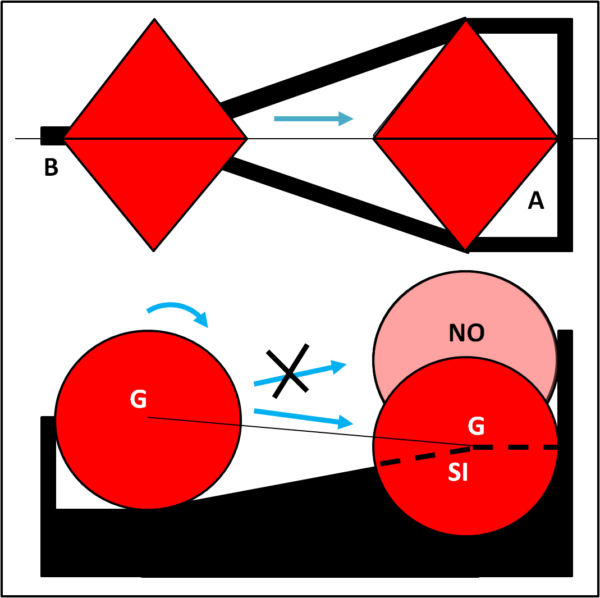
La spiegazione del paradosso è oltremodo semplice e basta una banale figura per risolvere l'arcano.

La inserisco in forma "nascosta" per lasciarvi la possibilità di  riflettere e arrivarci da soli.

Basta, infatti, ricordarsi la proprietà del baricentro di un qualsiasi corpo omogeneo, che riporto pari pari prendendola da Wikipedia:

In fisica il baricentro è il punto al quale è applicata la forza risultante di tutte le forze peso parallele. 

E poi riflettere sul suo movimento in un campo gravitazionale come è quello della Terra.

 

Se fate fatica a credere che il baricentro sia capace di questo, mettetevi comodi e imparate QUI come vincere una regata velica senza vento!

E se vi piacciono i paradossi, non potete perdervi QUESTI TRE!